Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
0.42m from the mass of 0.3kg
0.70m from the mass of 0.7kg
0.98m from the mass of 0.3kg
0.98m from the mass of 0.7kg
The correct Answer is:C
To solve the problem of finding the point on the rod through which the axis should pass to minimize the work required for rotation, we will follow these steps:
Step 1: Understand the System
We have two point masses, m1=0.3kg and m2=0.7kg, fixed at the ends of a rod of length L=1.4m. The goal is to find the position along the rod where the axis of rotation should be placed to minimize the work done for rotation.
Step 2: Define the Center of Mass
The center of mass (CM) of a system of point masses can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
where x1 and x2 are the positions of the masses. We can set x1=0 (position of m1) and x2=1.4m (position of m2).
Step 3: Substitute the Values
Substituting the values into the center of mass formula:
xcm=(0.3kg⋅0)+(0.7kg⋅1.4m)0.3kg+0.7kg
xcm=0+0.98kg m1.0kg=0.98m
Step 4: Interpret the Result
The center of mass is located at a distance of 0.98m from the 0.3kg mass. This is the point on the rod through which the axis of rotation should pass to minimize the work required for rotation.
Step 5: Conclusion
Thus, the point on the rod through which the axis should pass is located at a distance of 0.98m from the 0.3kg mass.
---
We have two point masses, m1=0.3kg and m2=0.7kg, fixed at the ends of a rod of length L=1.4m. The goal is to find the position along the rod where the axis of rotation should be placed to minimize the work done for rotation.
The center of mass (CM) of a system of point masses can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
where x1 and x2 are the positions of the masses. We can set x1=0 (position of m1) and x2=1.4m (position of m2).
Substituting the values into the center of mass formula:
xcm=(0.3kg⋅0)+(0.7kg⋅1.4m)0.3kg+0.7kg
xcm=0+0.98kg m1.0kg=0.98m
The center of mass is located at a distance of 0.98m from the 0.3kg mass. This is the point on the rod through which the axis of rotation should pass to minimize the work required for rotation.
Thus, the point on the rod through which the axis should pass is located at a distance of 0.98m from the 0.3kg mass.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - MCQ_TYPE
14 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Point masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :
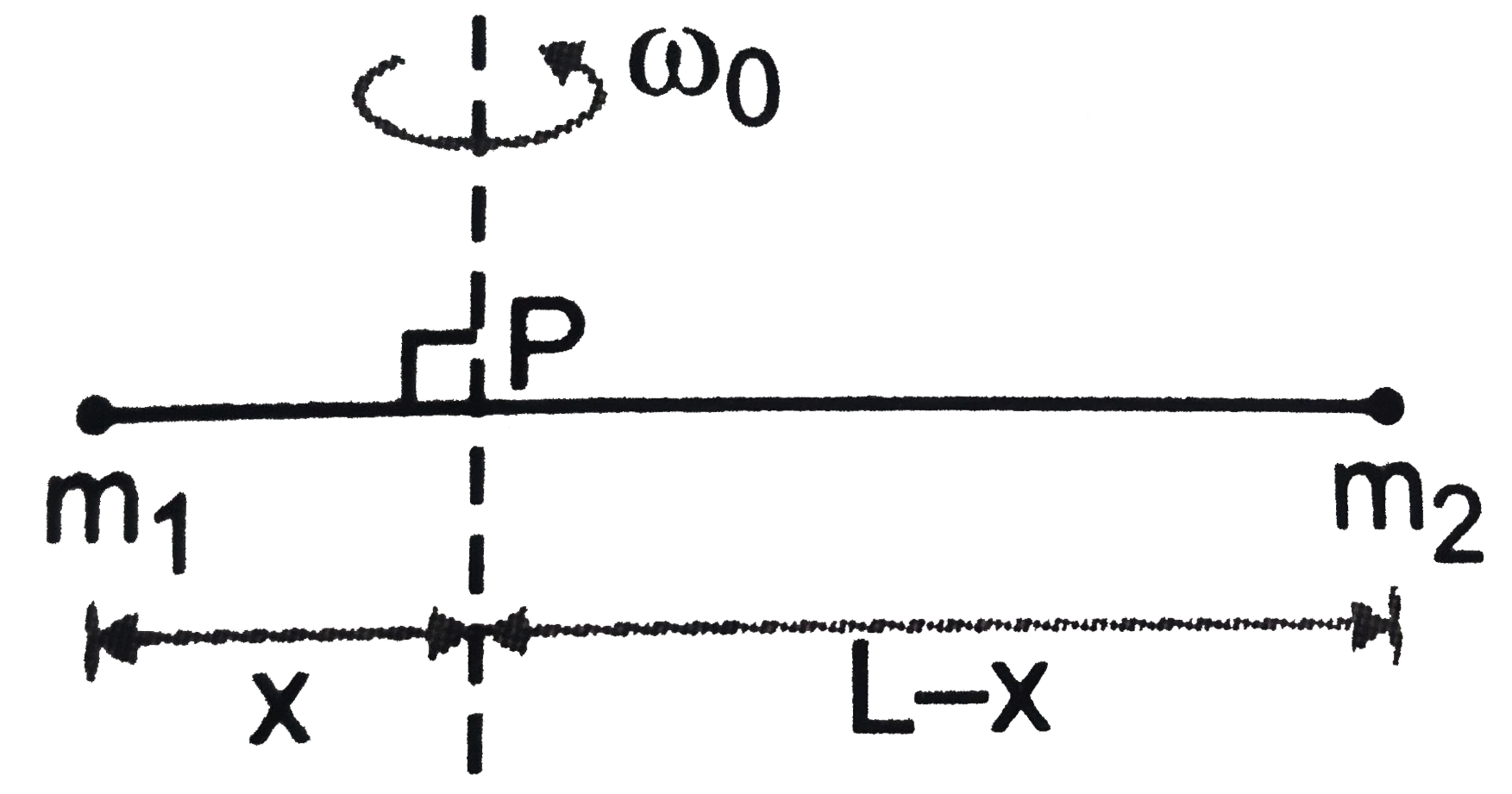
View SolutionTwo small spheres of mass 5kg and 15kg are joined by a rod of length 0.5m and of negligible mass. The M.I. of the system about an axis passing through centre of rod and normal to it is
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
The moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its centre will be
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View Solution
