Water is retained by a curved gate AB. Compute the horizontal and vertical component of the resultant of the hydrostatic pressure dsitribution on the gate AB, which is a quarter of a cylinder. Assume that the gate is 4m wide.

a. Horizontal component. The horizontal component of the resultant force on the gate is equal to the force on the vertical projection BA' of the gate. The pressure at a depth y from the free surface of the water is P=ρgy. The force on the strip of area 4dy of the gate is ,
dFH=P(4dy)=ρgy(4dy)=4ρydy

Total horizontal force is
FH=4ρg∫1510ydy=4ρg∣∣∣y22∣∣∣1510
=4×1000×10(152−1022)=250×104N
b. Vertical component : It is equal to the weight of the water above the curved surface. Dividing the volume above the curved surface into a rectangular parallelepiped and a quarder cylinder, we thus have

Fv= weight of water in DEFB+ Weight of water in ACBF
=ρ[V1+V2]g=1000[10×4×4+π(5)2×44]×10
[8×π]×104N
After calculating the values of Fv and FH we can calculate the resultant force on the gate F=√F2H+F2V
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
During a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
View SolutionA thermocol vessel contains 0.5kg of distilled water at 30∘C. A metal coil of area 5×10−3m2, number of turns 100, mass 0.06kg and resistance 1.6Ω is lying horizontally at the bottom of the vessel. A uniform time-varying magnetic field is set up to pass vertically through the coil at time t=0. The field is first increased from zero to 0.8T at a constant rate between 0 and 0.2s and then decreased to zero at the same rate between 0.2and0.4s. the cycle is repeated 12000 times. Make sketches of the current through the coil and the power dissipated in the coil as function of time for the first two cycles. Clearly indicate the magnitude of the quantities on the axes. Assumes that no heat is lost to the vessel or the surroundings. Determine the final tempreture of water under thermal equilibrium. Specific heat of metal =500jkg−1K−1 and the specific heat of water =4200jkg−1K−1. Neglect the inductance of coil.
View SolutionA horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
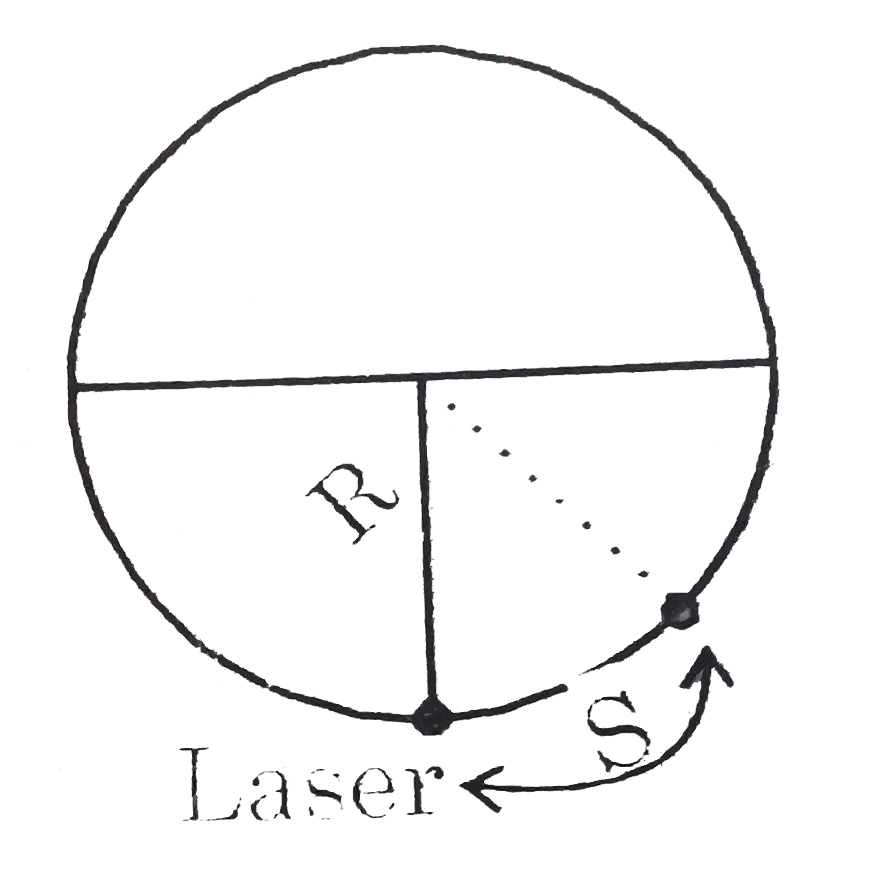
View SolutionA rod AB length 5m which remains in vertical plane has its ends A and B constrained to remain contact with a horizontal floor and a vertical wall respectively. Determine the velocity of the end B and angular velocity at the position shown in Fig. , if the point A has a velocity of 3ms1rightward.

View SolutionA particle is moving along a vertical circle of radius R=20m with a constant speed v=31.4m/s as shown in the figure. Straight line ABC is horizontal and passes through the centre of the circle. A shell is fired from point A at the instant when particle is at C. The distance AB is 20√3m and shell collides with the particle at B, if smallest possible value of the angle of projection is k×10∘ then find the value of k.

View SolutionProblem on sine rule Type:-2 (i)The angle of elevation of the top of the tower from a point A due South of the tower is α and from B due east of the tower is β. If AB=d Show that the height of the tower is d√cot2α+cot2β (ii) A tree stands vertically on a hill side which makes an angle of 15∘ with the horizontal. From a point on the ground 35m down the hill from the base of the tree ; the angle of elevation of the top of the tree is 60∘ .find the height of the tree ?
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
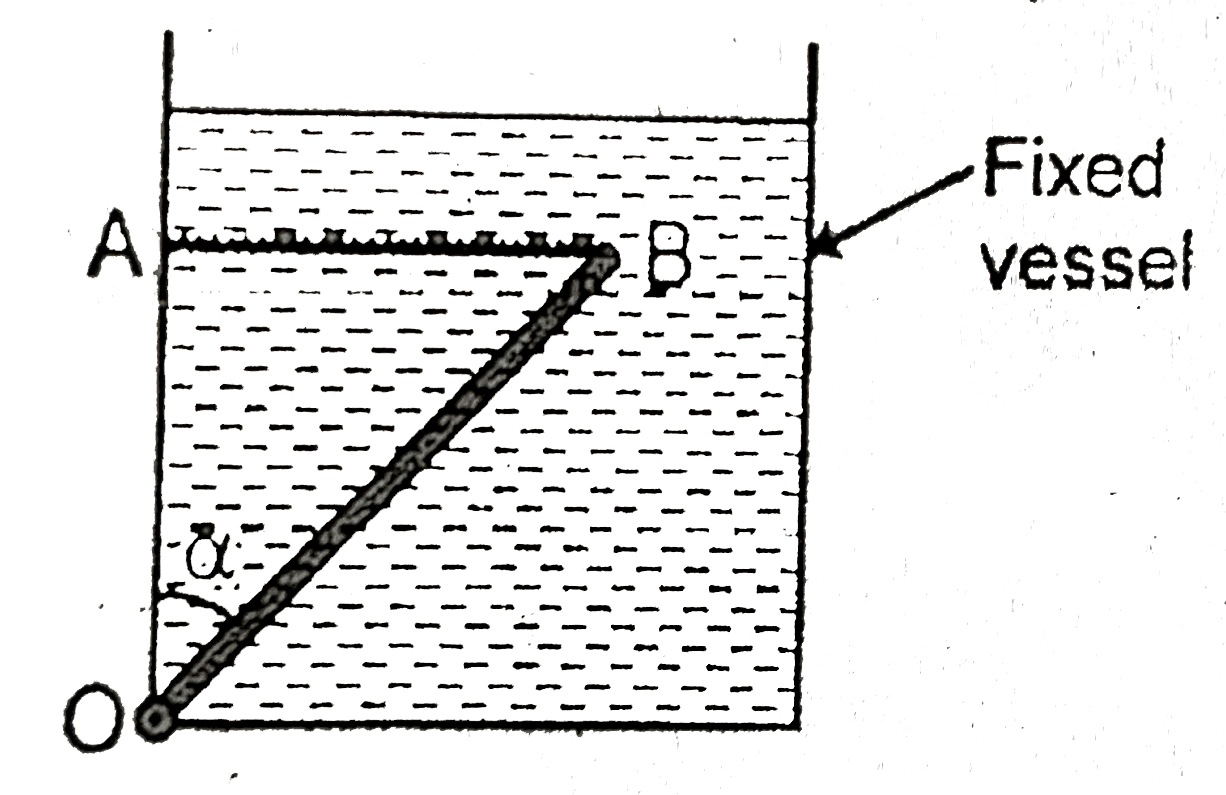
View SolutionA uniform rod OB of length 1m, cross-sectional areal 0.012m2 and relative density 2.0 is free to rotate about smooth hinge O in vertical plane. The rod is held with a horizontal string AB which can withstand a maximum tension of 45N. The rod and string system is kept in water as shown in figure. The maximum value of angle α which the rod can make with vertical without breaking the string is
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionA unifrom rod AB of length 4m and mass 12kg is thrown such that just after the projection the centre of mass of the rod moves vertically upwards with a velocity 10m/s and at the same time its is rotating with an angular velocity π2rad/sec about a horizontal axis passing through its mid point. Just after the rod is thrown it is horizontal and is as shown in the figure. Find the acceleration (in m/sec2) of the point A in m/s2 when the centre of mass is at the highest point. (Take =10m/s2 and π2=10)

View Solution
