Question

Consider a container having an inclined wall, inclined an angle $\theta$ with horizontal as shown in Fig. Calculate the force per unit width on the wall.

Explanation

Since pressure always gets normal to the suface therefore the pressure diagram for an inclined wall is shown in Figure. The base of the triangular presure diagram is equal to `rhoghH` because pressure at a point depends on the height of liquid column above it.

The total of application of the total force is through the centroid of the pressure diagram as shown in figure.
Alternatively the force on the inclined wall may be obtained in two parts horizontal and vertical.
The horizontal force `F_(x)` acts on the vertical projection of the inclined wall.

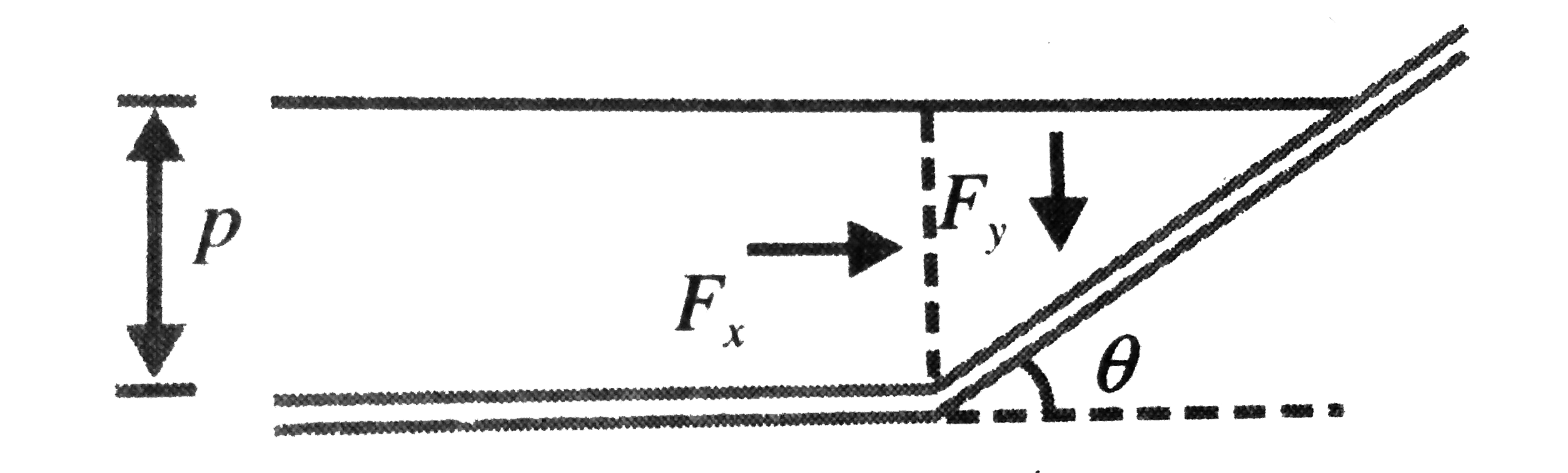
`F_(x)=1/2rhoghbH^(2)`
The vertical force `F_(v)` acts due to the weight of the liquid supported by the wall
`F_(y)=1/2rhogb(H)(hcottheta)=1/2rhoghH^(2)cot^(2)theta`
The magnitude of the resultant force is
`F=sqrt(F_(x)^(2)-F_(y)^(2))=1/2rhogbH^(2)cosectheta`
`impliesF/b=1/2rhogH^(2)/(sintheta)`