Figure shows a semi-cylindrical massless gate pivoted at the point $O$ holding a stationary liquid of density $ρ$ . The length of the cylinder is $l$ . Calculate, the horizontal force exerted by the liquid on the gate.

Text Solution

Verified by Experts

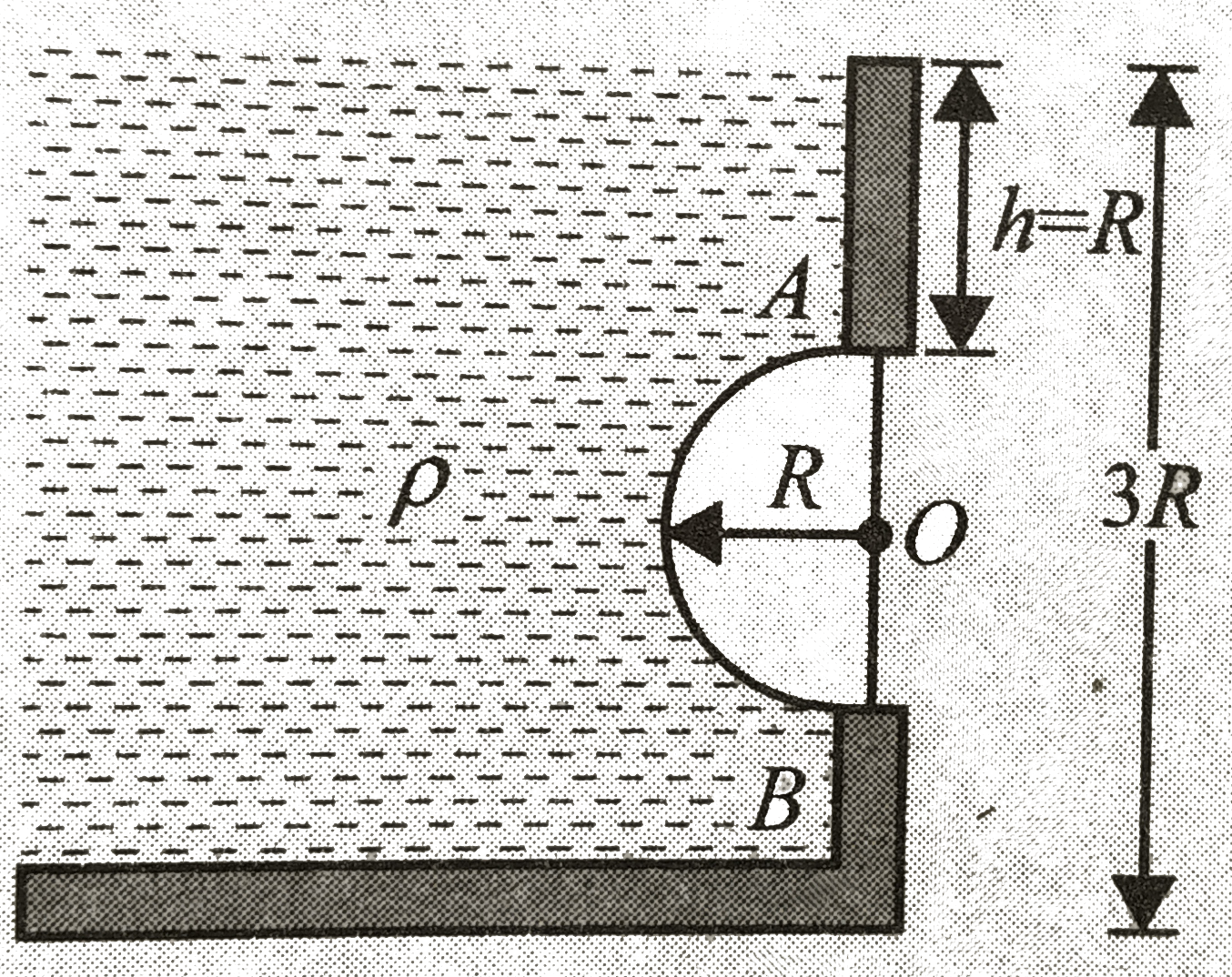
The force exerted by liquid on the gate is
$f_{H} = P_{a v} \times$ vertical projection area of the gate
$= (\frac{P_{A} - P_{B}}{2}) \times (2 R l)$
$= (\frac{R ρ g + 3 R ρ g}{2}) \times 2 R l = 4 ρ g R^{2} l$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

The fig shows a semo-cylinderical massless gate of unit length perpendicular to the plane of the page and is pivoted at the point $O$ holding a stationary liquid of density $ρ$ . A horizontal foce $F$ is applied at its lowest position to keep it stationary. The magnitude of the force is:
A $\frac{3}{2} ρ g R^{2}$
B $\frac{9}{2} ρ g R^{2}$
C $ρ g R^{2}$
D $2 ρ g R^{2}$
Question 2 - Select One
A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density $ρ$ . The force F required to prevent the rotation of the gate is equal to

A $2 π R^{3} ρ g$
B $2 ρ g R^{3}$
C $\frac{2 R^{2} ρ g}{3}$
DNone of these
Question 3 - Select One or More
A liquid of density $ρ$ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F :
A $F \propto v$
B $F \propto v^{2}$
C $F \propto A$
D $F \propto ρ$

CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-Exercise 4.1

Home
Ask Doubt
Profile