The minimum horizontal acceleration of the container4 so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
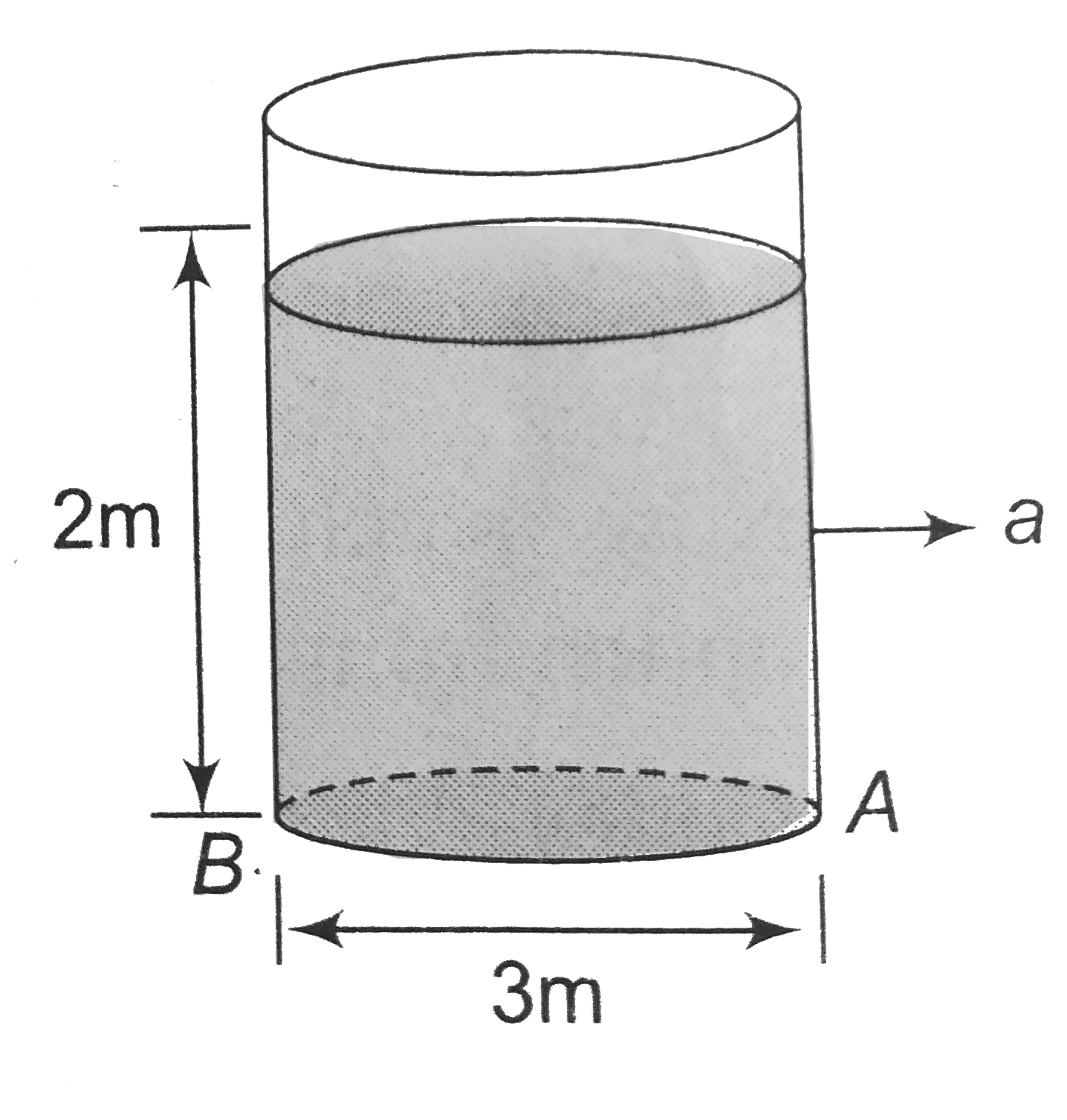
32g
43g
42g
34g
The correct Answer is:B
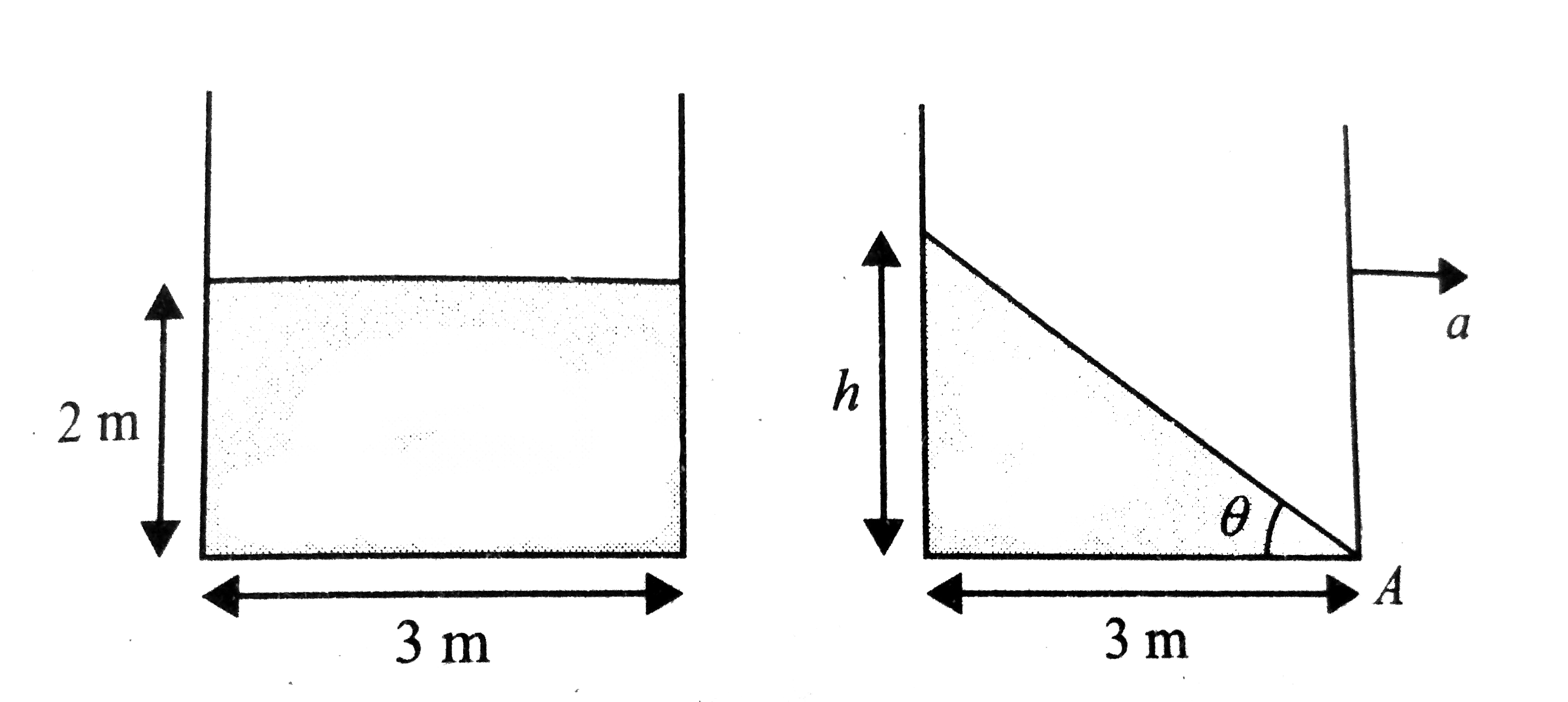
Volume equality gives
2×3=12×h×3⇒h=4m
∴tanθ=43=ag⇒a=43g
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The minimum horizontal acceleration of the container a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
 View Solution
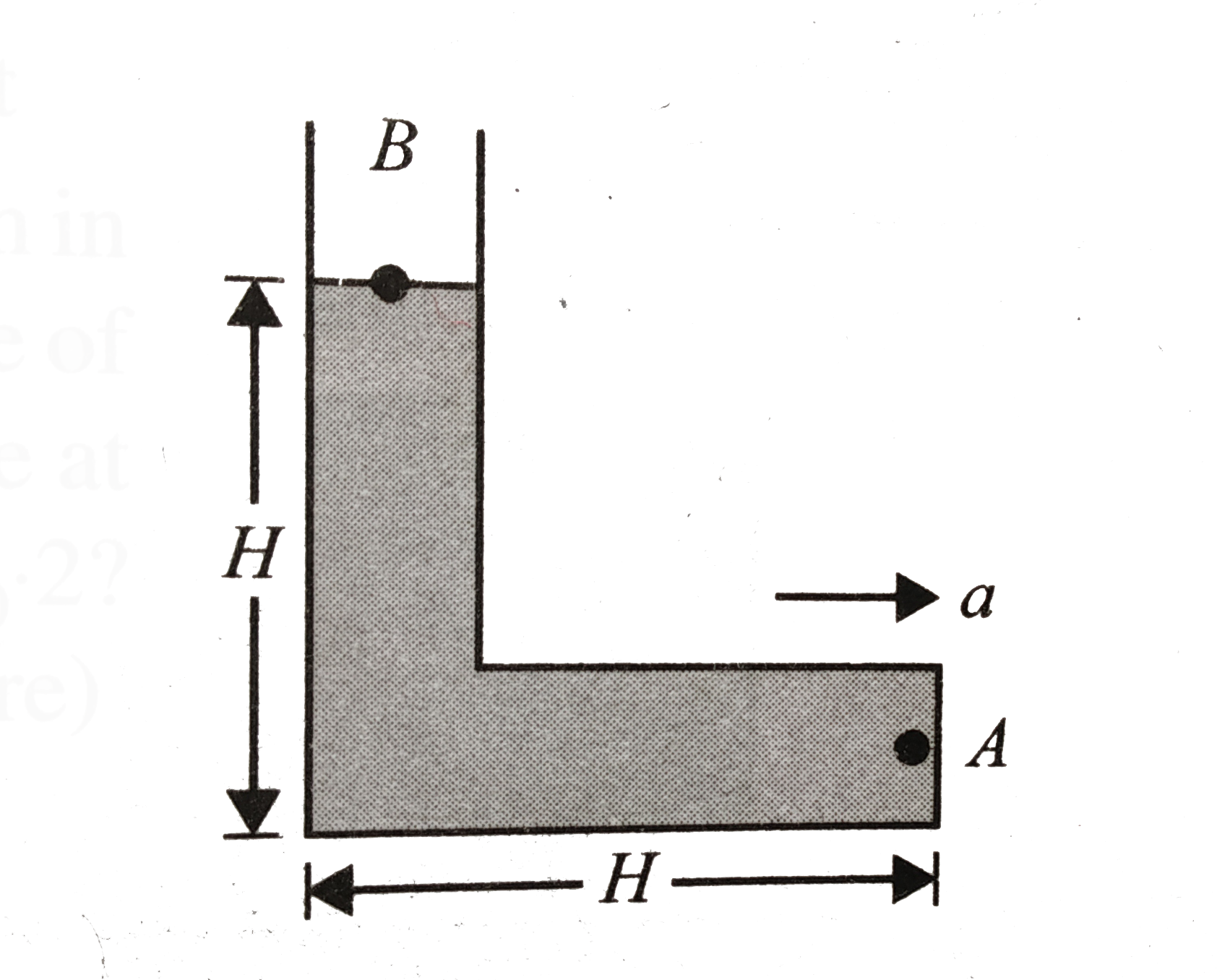
View SolutionFigure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.
 View Solution
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)
 View Solution
View SolutionFor the L-shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point A becomes equal to p02? (p0 is the atmospheric pressure)
 View Solution
View SolutionA U-tube of base length l filled with the same volume of two liquids of densities ρ and 2ρ is moving with an acceleration 'a' on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then the height h is given by
 View Solution
View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case
 View Solution
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
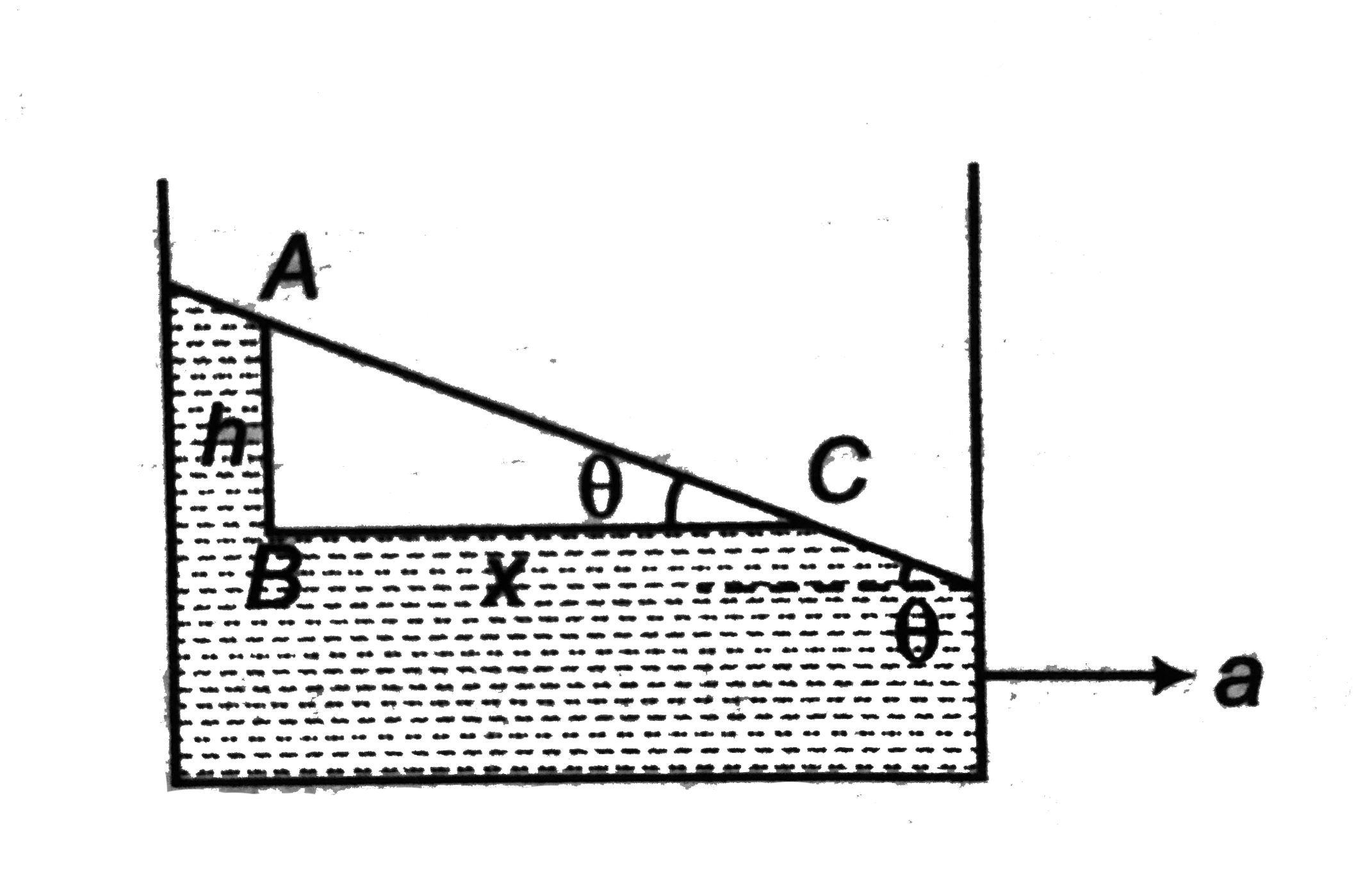
Using the pressure equation along the path ABC find the angle θ.View SolutionTwo containers A and B of equal volume V0/2 each are connected by a narrow tube which can be closed by a value. The containers are fitted with pistons which can be moved to change the volumes. Initially the value is open and the containers contain an ideal gas (Cp/Cv=γ) at atmospheric pressure P0 and atmospheric temperature 2T0. The walls of the containers A are highly conducting and of B are non-conducting. The value is now closed and the pistons are slowly pulled out to increase the volumes of the containers to double the original value. (a) Calculate the temperature and pressure in the two containers. (b) The value is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and the pressure.
View SolutionAn ideal gas is pumped into a rigid container having diathermic walls so that the temperature remains constant. In a certain time interval, the pressure in the container is doubled. Is the internal energy of the contains of the container also doubled in the interval?
View Solution

