A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom the pot. Find the maximum weight that can be put on the block without wetting the new weight. Density of wood=800kg/m3 and spring constant of the spring =50N/m.(Take g=10m/s2)

a(a2ρg+K)
a(aρg+2K)
a(aρg2+2K)
a(a2ρg+K2)
The correct Answer is:D
Since density of block =12 (density of water), 50% of its volume is immersed in water.
In the second case half of the volume of the block is futher immersed in water. 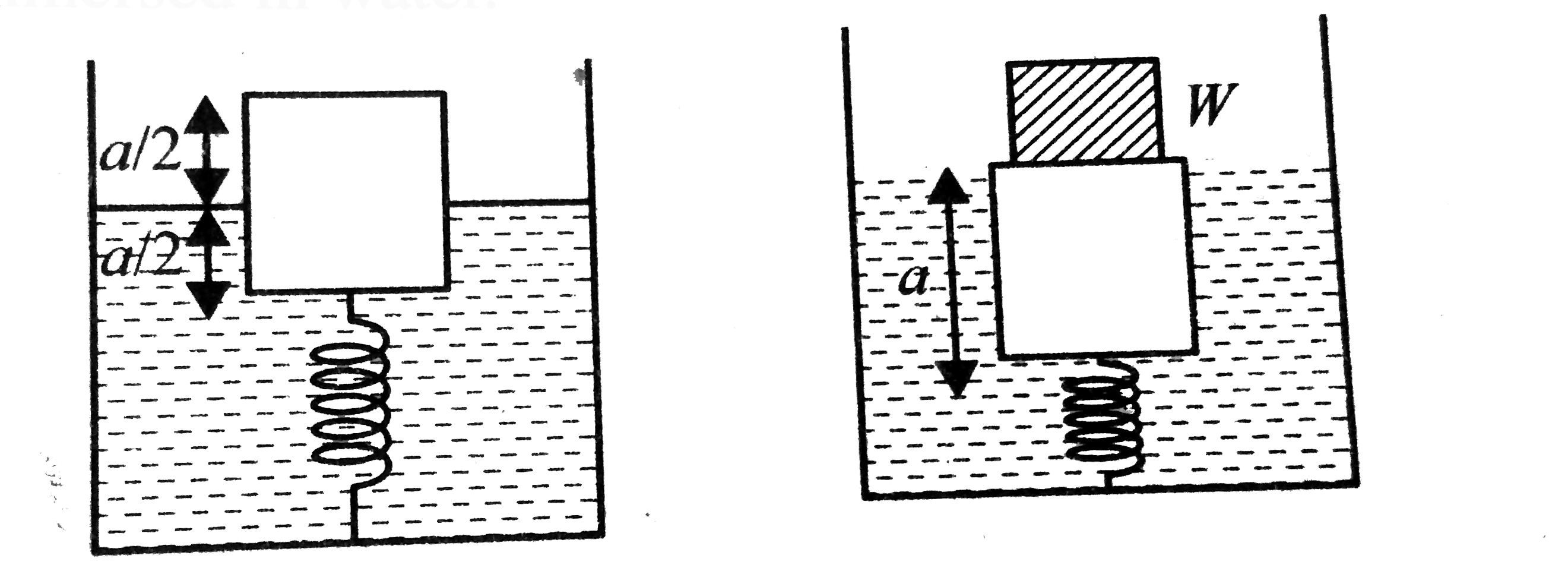
Therefore W= Extra uptrust + Spring force
=a×a×a2×2ρ×g+K(a2)
=a(a2ρg+K2)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cubical block of side 0.5 M floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take density of water =103kg/m3]
View SolutionA log of wood of mass 120 Kg floats in water. The weight that can be put on the raft to make it just sink, should be (density of wood =600Kg/m)
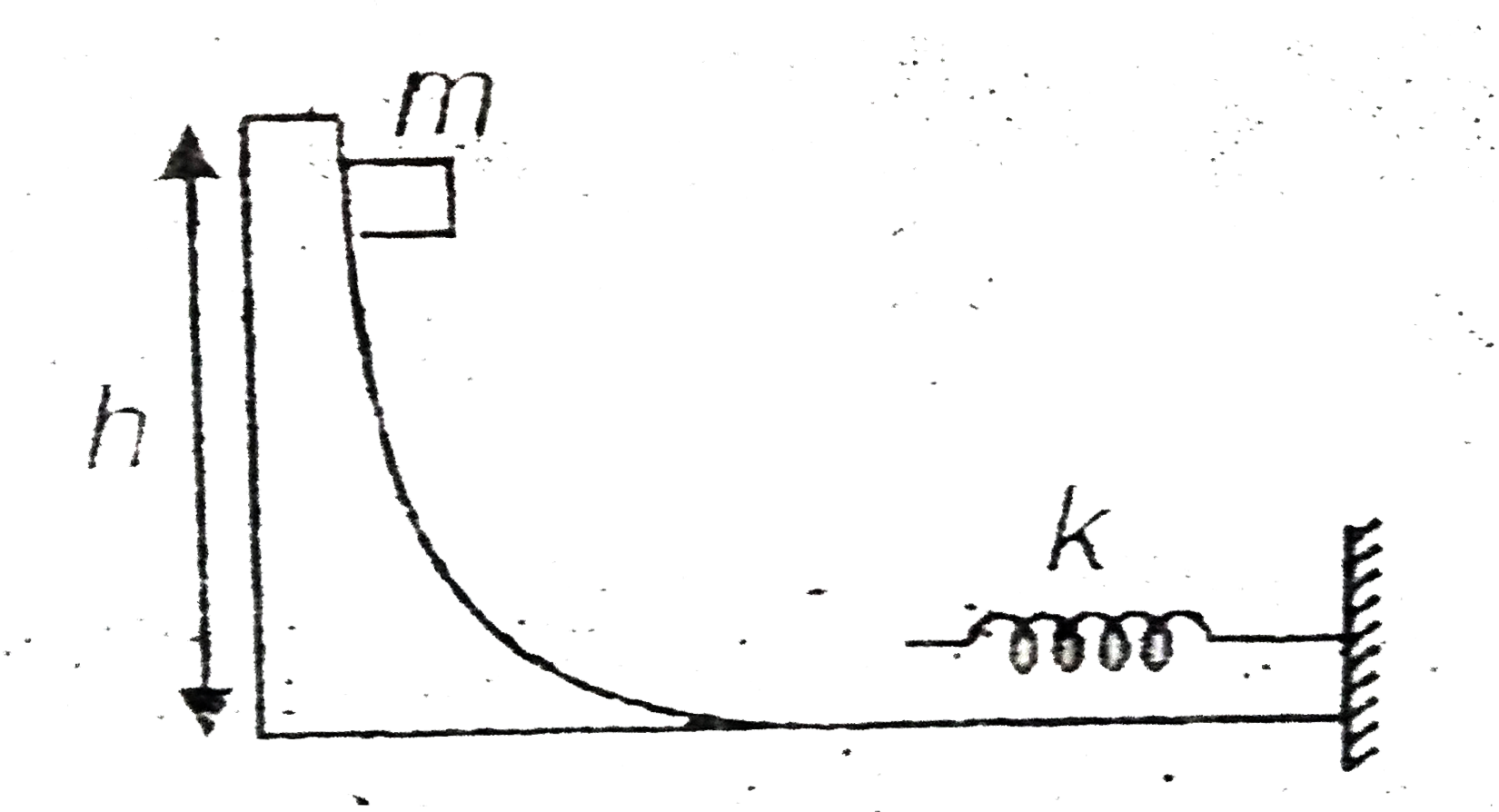
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View SolutionA cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA block of wood of mass 24 kg floats in water. The volume of wood is 0.032 m^3. Find the density of wood. (Density of water = 1000kg m−3 )
View SolutionA raft of wood (density=600kg/m3) of mass 120kg floats in water. How much weight can be put on the raft to make it just sink?
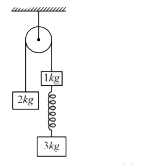
View SolutionFrom the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
View Solution
