A horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
a1a2√2gha21−a22
a1a2√2gh(a21−a22)
a1a2 ⎷(a21+a22)h2g(a21−a22)
2a1a2gh√a21−a22
The correct Answer is:A
To find the flow rate of the liquid in the horizontal tube with different cross sections at points A and B, we can follow these steps:
Step 1: Understand the Given Information
We are given:
- Cross-sectional areas at points A and B: A1 and A2
- Pressures at points A and B: p1=ρgh1 and p2=ρgh2
- The difference in height of the liquid columns: h=h1−h2
Step 2: Apply Bernoulli's Equation
According to Bernoulli's principle, for incompressible flow, we have:
p1+12ρv21+ρgh1=p2+12ρv22+ρgh2
Substituting the pressures:
ρgh1+12ρv21=ρgh2+12ρv22
Step 3: Rearranging the Equation
Rearranging the equation gives:
ρgh1−ρgh2=12ρv22−12ρv21
Factoring out ρ:
ρg(h1−h2)=12ρ(v22−v21)
Since h1−h2=h:
ρgh=12ρ(v22−v21)
Step 4: Canceling Out Density
Dividing through by ρ:
gh=12(v22−v21)
Multiplying through by 2:
2gh=v22−v21
Step 5: Expressing Velocity
Rearranging gives:
v22=v21+2gh
Step 6: Using Continuity Equation
From the continuity equation, we know:
A1v1=A2v2
Thus, we can express v1 in terms of v2:
v1=A2A1v2
Step 7: Substitute v1 into the Velocity Equation
Substituting v1 into the equation for v22:
v22=(A2A1v2)2+2gh
This simplifies to:
v22=A22A21v22+2gh
Step 8: Rearranging to Solve for v2
Rearranging gives:
v22(1−A22A21)=2gh
Factoring out v22:
v22(A21−A22A21)=2gh
Thus:
v22=2ghA21A21−A22
Step 9: Finding the Volume Flow Rate
The volume flow rate Q is given by:
Q=A2v2
Substituting for v2:
Q=A2
⎷2ghA21A21−A22
Final Expression for Flow Rate
Thus, the flow rate of the liquid in the horizontal tube is:
Q=A2
⎷2ghA21A21−A22
We are given:
- Cross-sectional areas at points A and B: A1 and A2
- Pressures at points A and B: p1=ρgh1 and p2=ρgh2
- The difference in height of the liquid columns: h=h1−h2
According to Bernoulli's principle, for incompressible flow, we have:
p1+12ρv21+ρgh1=p2+12ρv22+ρgh2
Substituting the pressures:
ρgh1+12ρv21=ρgh2+12ρv22
Rearranging the equation gives:
ρgh1−ρgh2=12ρv22−12ρv21
Factoring out ρ:
ρg(h1−h2)=12ρ(v22−v21)
Since h1−h2=h:
ρgh=12ρ(v22−v21)
Dividing through by ρ:
gh=12(v22−v21)
Multiplying through by 2:
2gh=v22−v21
Rearranging gives:
v22=v21+2gh
From the continuity equation, we know:
A1v1=A2v2
Thus, we can express v1 in terms of v2:
v1=A2A1v2
Substituting v1 into the equation for v22:
v22=(A2A1v2)2+2gh
This simplifies to:
v22=A22A21v22+2gh
Rearranging gives:
v22(1−A22A21)=2gh
Factoring out v22:
v22(A21−A22A21)=2gh
Thus:
v22=2ghA21A21−A22
The volume flow rate Q is given by:
Q=A2v2
Substituting for v2:
Q=A2
⎷2ghA21A21−A22
Thus, the flow rate of the liquid in the horizontal tube is:
Q=A2
⎷2ghA21A21−A22
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then

View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
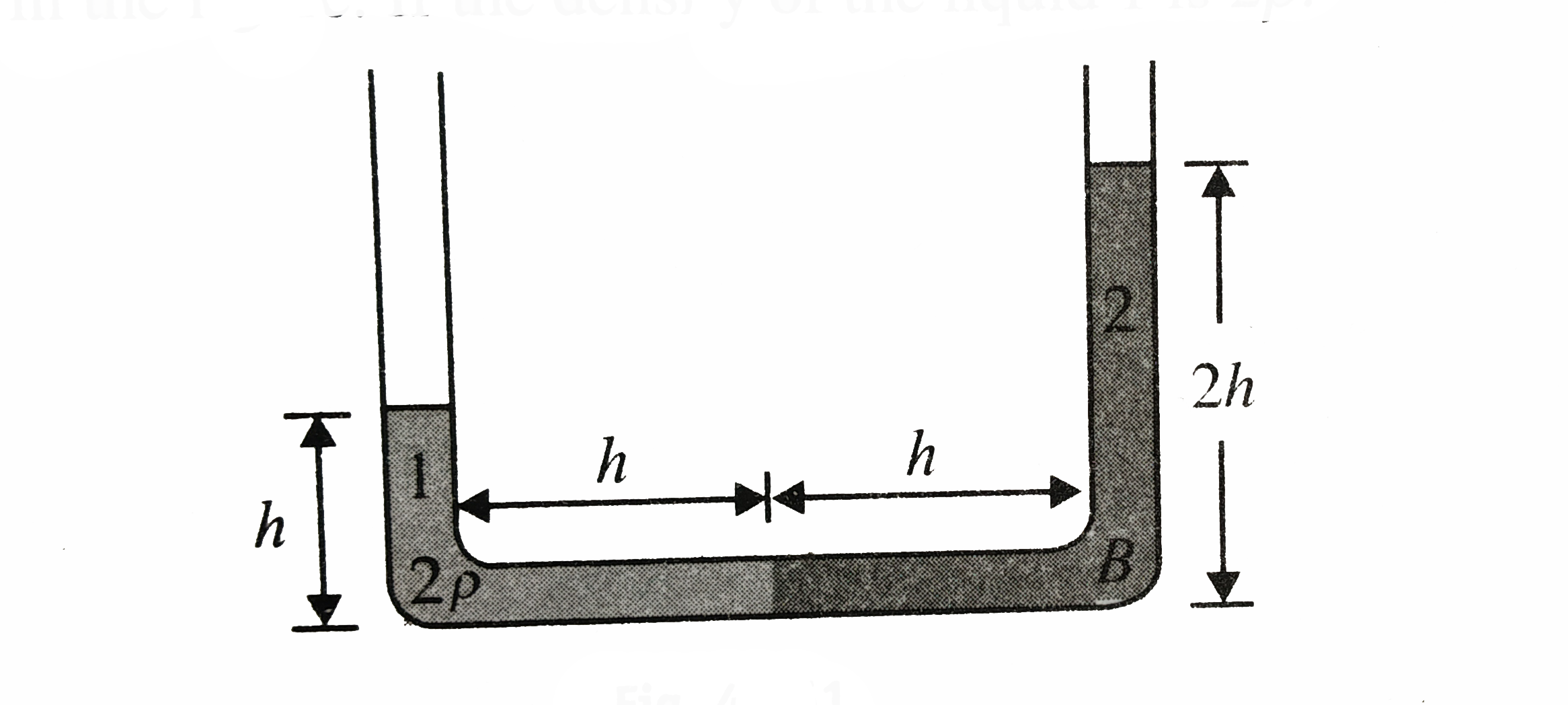
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View SolutionIn a capillary tube having area of cross - section A, water rises to a height h. If cross-sectional area is reduced to A9, the rise of water in the capillary tube is
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View SolutionWater flows through a horizontal tube of variable cross-section. The area of cross section at A and B are 4mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionWater flows through a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per second through A find
a) The speed of water at A
b) the speed of river at B
c) the pressure difference PA−PB.

View SolutionWater flows in a horizontal tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B where the areas of cross section are 30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
 ,
,
View Solution
