The water flowing through the same tube having two different cross section areas has different flow rates .
To solve the problem regarding the flow of water through a tube with two different cross-sectional areas and different flow rates, we can use the principle of conservation of mass, specifically the equation of continuity for incompressible fluids.
1. Understand the Concept of Flow Rate:
The flow rate (Q) of a fluid is defined as the volume of fluid that passes through a cross-section of the tube per unit time. It can be expressed as:
Q=A⋅v
where A is the cross-sectional area and v is the velocity of the fluid.
2. Apply the Equation of Continuity:
According to the equation of continuity for incompressible fluids, the flow rate must remain constant along a streamline. This can be mathematically expressed as:
A1v1=A2v2
where:
- A1 is the cross-sectional area at point 1,
- v1 is the velocity at point 1,
- A2 is the cross-sectional area at point 2,
- v2 is the velocity at point 2.
3. Identify the Areas:
Given that the tube has two different cross-sectional areas, let’s denote them as A1 and A2. Since these areas are different, we can say:
A1≠A2
4. Analyze the Implications:
Since the areas are different, the equation A1v1=A2v2 implies that if A1 is larger than A2, then v1 must be less than v2 to maintain the equality. Conversely, if A1 is smaller than A2, then v1 must be greater than v2.
5. Conclusion:
Therefore, the water flowing through the tube with different cross-sectional areas will have different velocities, leading to different flow rates. This confirms that the flow rates are indeed different due to the varying cross-sectional areas.
Final Answer:
The water flowing through the same tube with two different cross-sectional areas has different flow rates, as indicated by the equation of continuity: A1v1=A2v2.
---
The flow rate (Q) of a fluid is defined as the volume of fluid that passes through a cross-section of the tube per unit time. It can be expressed as:
Q=A⋅v
where A is the cross-sectional area and v is the velocity of the fluid.
According to the equation of continuity for incompressible fluids, the flow rate must remain constant along a streamline. This can be mathematically expressed as:
A1v1=A2v2
where:
- A1 is the cross-sectional area at point 1,
- v1 is the velocity at point 1,
- A2 is the cross-sectional area at point 2,
- v2 is the velocity at point 2.
Given that the tube has two different cross-sectional areas, let’s denote them as A1 and A2. Since these areas are different, we can say:
A1≠A2
Since the areas are different, the equation A1v1=A2v2 implies that if A1 is larger than A2, then v1 must be less than v2 to maintain the equality. Conversely, if A1 is smaller than A2, then v1 must be greater than v2.
Therefore, the water flowing through the tube with different cross-sectional areas will have different velocities, leading to different flow rates. This confirms that the flow rates are indeed different due to the varying cross-sectional areas.
The water flowing through the same tube with two different cross-sectional areas has different flow rates, as indicated by the equation of continuity: A1v1=A2v2.
Similar Questions
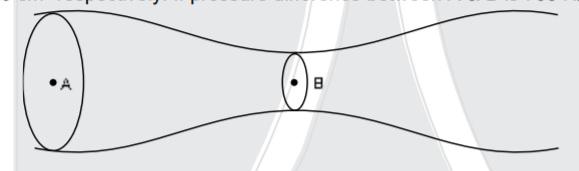
An ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is
View SolutionWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
View SolutionWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionIn this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.

View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View Solutionwater is flowing through a tube of non-uniform cross-section. If the radii of the tube at the entrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
View SolutionWater flows through a frictionless tube with a varying cross-section as shown

The variation of Pressure P as the fluid move through the pipe is correctly shown in
View SolutionThe difference of pressure between two points along a horizontal pipe through which water is flowing is 14cm of Hg. If due to non-uniform cross section the speed of flow at a point of greater cross section is 60cm/s, speed of flow at the other point is
View Solution
