Statement I: When a body floats such that its parts are immersed into two immiscible liquids, then force exerted by liquid 1 is of magnitude ρ1v1g.
Statement II: Total buoyant force =ρ1v1g+ρ2v2g.

Statement I is true, statement II is true and Statement II is a correct explanation for Statement I.
Statement I is true, Statement II is true and Statement II is NOT the correct explanation for Statement I.
Statement I is true, Statement II is false.
Statement I is false, Statement II is true.
The correct Answer is:D

ρ1v1g is not the force applied by liquid 1 on body it ρ1gh×A, although net force (buoyant) comes out of be ρ1v1g+ρ2v2g
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Linked Comprehension43videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the upper liquid is
 View Solution
View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body floats in a liquid A of density ρ1 with a part of it submerged inside liquid while in liquid B of density ρ2 totally submerged inside liquid. The densities ρ1 and ρ2 are related as :
Aρ1=ρ2Bρ1<ρ2Cρ1>ρ2Dnothing can be said
The light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.
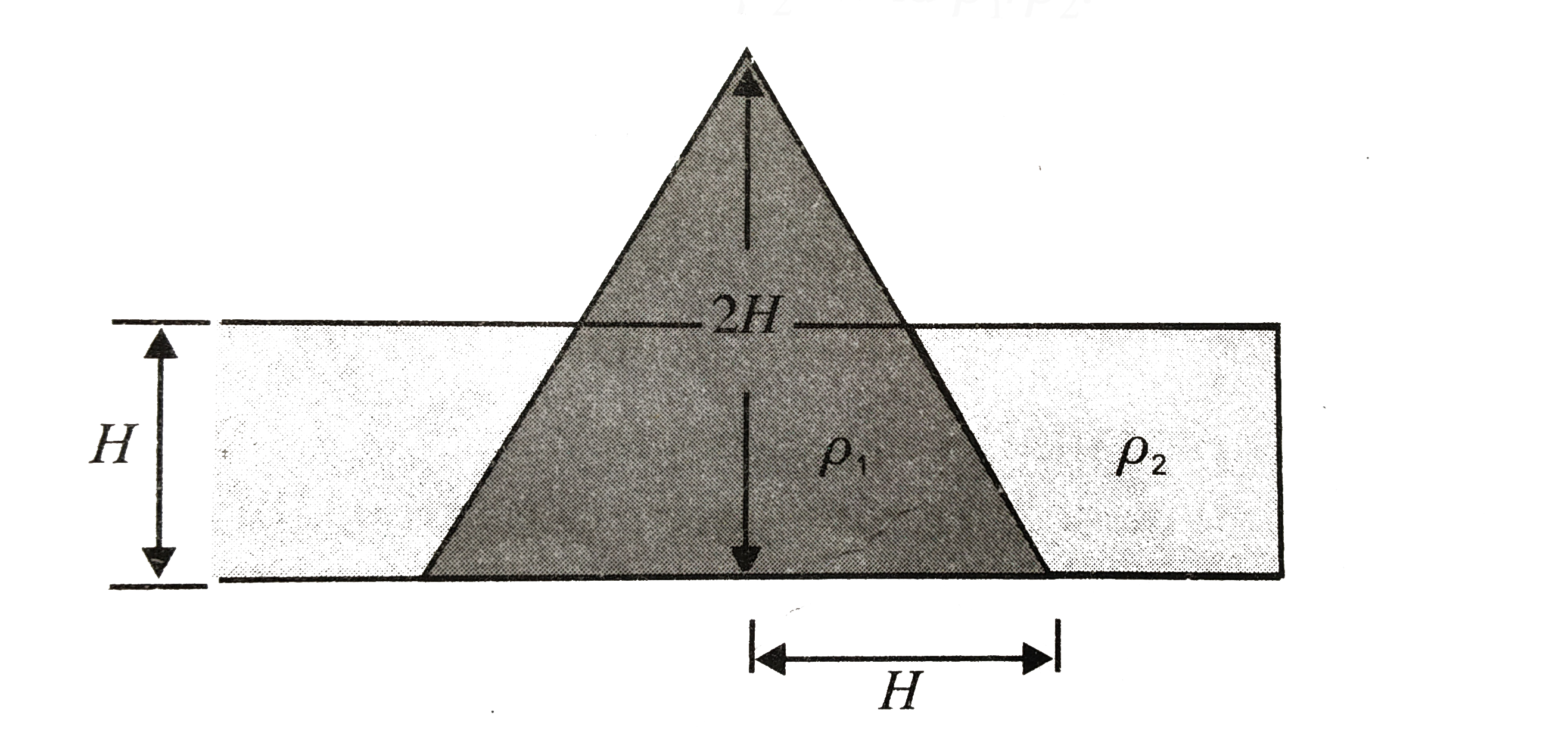 View Solution
View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.
 View Solution
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
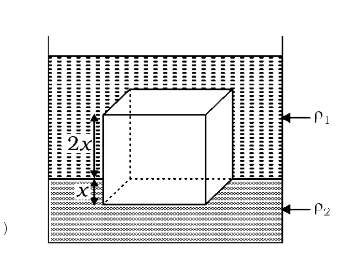 View Solution
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionThe velocities of sound at same temperature in two monoatomic gases densities ρ1 and ρ2 are v1 and v2 repectively , if ρ1ρ2=4, then the value of v1v2 will be
View SolutionA body of density ρ is immersed in a liquid of density ρL.State condition when the body will (i) float (ii) sink in liquid.
View Solution

