A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
ρ2−ρρ−ρ1
ρ+ρ1ρ+ρ2
ρ+ρ2ρ+ρ1
√ρ1ρ2ρ
To solve the problem of finding the ratio of the volumes of the parts of a solid sphere that are submerged in two immiscible liquids, we can follow these steps:
1. Understanding the Problem:
- We have a solid sphere with volume V and density ρ.
- The sphere is floating at the interface of two immiscible liquids with densities ρ1 (upper liquid) and ρ2 (lower liquid).
- Given that ρ1<ρ<ρ2, we need to find the ratio of the volumes of the sphere submerged in the upper liquid V1 and the lower liquid V2.
2. Applying the Principle of Buoyancy:
- The weight of the sphere is balanced by the buoyant forces from both liquids.
- The weight of the sphere is given by:
W=mg=ρVg
- The buoyant force from the upper liquid is:
F1=ρ1V1g
- The buoyant force from the lower liquid is:
F2=ρ2V2g
3. Setting Up the Equation:
- The equilibrium condition gives us:
ρVg=F1+F2
- Substituting the expressions for F1 and F2:
ρVg=ρ1V1g+ρ2V2g
- Cancel g from both sides:
ρV=ρ1V1+ρ2V2
4. Using Volume Conservation:
- The total volume of the sphere is the sum of the volumes submerged in both liquids:
V=V1+V2
5. Substituting for V2:
- From the volume conservation equation, we can express V2 as:
V2=V−V1
- Substitute V2 into the buoyancy equation:
ρV=ρ1V1+ρ2(V−V1)
- Expanding this gives:
ρV=ρ1V1+ρ2V−ρ2V1
- Rearranging terms leads to:
ρV−ρ2V=(ρ1−ρ2)V1
- Simplifying further:
V(ρ−ρ2)=V1(ρ1−ρ2)
6. Finding the Ratio V1V2:
- Rearranging gives:
V1=V(ρ−ρ2)ρ1−ρ2
- Using V2=V−V1:
V2=V−V(ρ−ρ2)ρ1−ρ2=V(1−ρ−ρ2ρ1−ρ2)
- Therefore, the ratio V1V2 becomes:
V1V2=V(ρ−ρ2)ρ1−ρ2V(1−ρ−ρ2ρ1−ρ2)
- Simplifying this gives:
V1V2=ρ−ρ2ρ1−ρ
7. Final Result:
- Thus, the ratio of the volumes of the parts of the sphere in the upper and lower liquid is:
V1V2=ρ−ρ1ρ2−ρ
- We have a solid sphere with volume V and density ρ.
- The sphere is floating at the interface of two immiscible liquids with densities ρ1 (upper liquid) and ρ2 (lower liquid).
- Given that ρ1<ρ<ρ2, we need to find the ratio of the volumes of the sphere submerged in the upper liquid V1 and the lower liquid V2.
- The weight of the sphere is balanced by the buoyant forces from both liquids.
- The weight of the sphere is given by:
W=mg=ρVg
- The buoyant force from the upper liquid is:
F1=ρ1V1g
- The buoyant force from the lower liquid is:
F2=ρ2V2g
- The equilibrium condition gives us:
ρVg=F1+F2
- Substituting the expressions for F1 and F2:
ρVg=ρ1V1g+ρ2V2g
- Cancel g from both sides:
ρV=ρ1V1+ρ2V2
- The total volume of the sphere is the sum of the volumes submerged in both liquids:
V=V1+V2
- From the volume conservation equation, we can express V2 as:
V2=V−V1
- Substitute V2 into the buoyancy equation:
ρV=ρ1V1+ρ2(V−V1)
- Expanding this gives:
ρV=ρ1V1+ρ2V−ρ2V1
- Rearranging terms leads to:
ρV−ρ2V=(ρ1−ρ2)V1
- Simplifying further:
V(ρ−ρ2)=V1(ρ1−ρ2)
- Rearranging gives:
V1=V(ρ−ρ2)ρ1−ρ2
- Using V2=V−V1:
V2=V−V(ρ−ρ2)ρ1−ρ2=V(1−ρ−ρ2ρ1−ρ2)
- Therefore, the ratio V1V2 becomes:
V1V2=V(ρ−ρ2)ρ1−ρ2V(1−ρ−ρ2ρ1−ρ2)
- Simplifying this gives:
V1V2=ρ−ρ2ρ1−ρ
- Thus, the ratio of the volumes of the parts of the sphere in the upper and lower liquid is:
V1V2=ρ−ρ1ρ2−ρ
Similar Questions
A solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
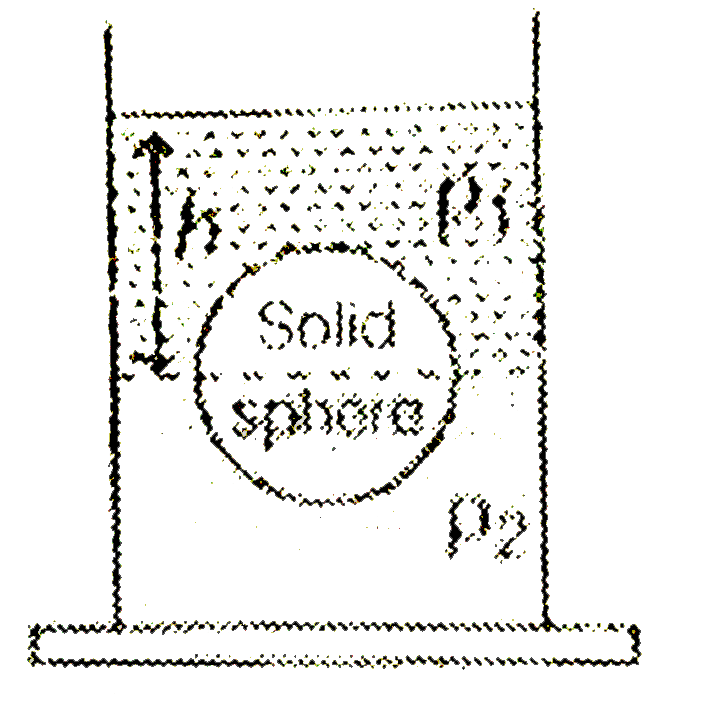
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View Solutionv1andv2 are the velocities of sound at the same temperature in two monoatomic gases of densities ρ1andρ2 respectively. If ρ1ρ2=14 then the ratio of velocities v1andv2 is
View SolutionThe light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.

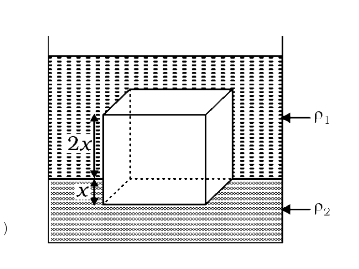
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
View SolutionThe velocities of sound at same temperature in two monoatomic gases densities ρ1 and ρ2 are v1 and v2 repectively , if ρ1ρ2=4, then the value of v1v2 will be
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionA ball of density ρ is dropped from a height on the surface of a non-viscous liquid of density 2ρ. Choose the correct options.

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the upper liquid is

View Solution
