A uniform rod of length $L$ pivoted at the bottom of a pond of depth $L / 2$ stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass $m$ of the rod.

A

$(\sqrt{2} - 1) m g$

B

$(\sqrt{2} + 1) m g$

C

$(\sqrt{3} + 1) m g$

D

$(\sqrt{2} + 3) m g$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Weight of the rod $w = L A ρ g$
( $A =$ area of cross section $ρ =$ density of material)
Submerged length of the given by
$O T = \frac{L}{2 sin θ}$
Buoyant force $B = (\frac{L}{2 sin θ}) A ρ_{w} g$
From Archimedes' principle ( $ρ w =$ density of water).

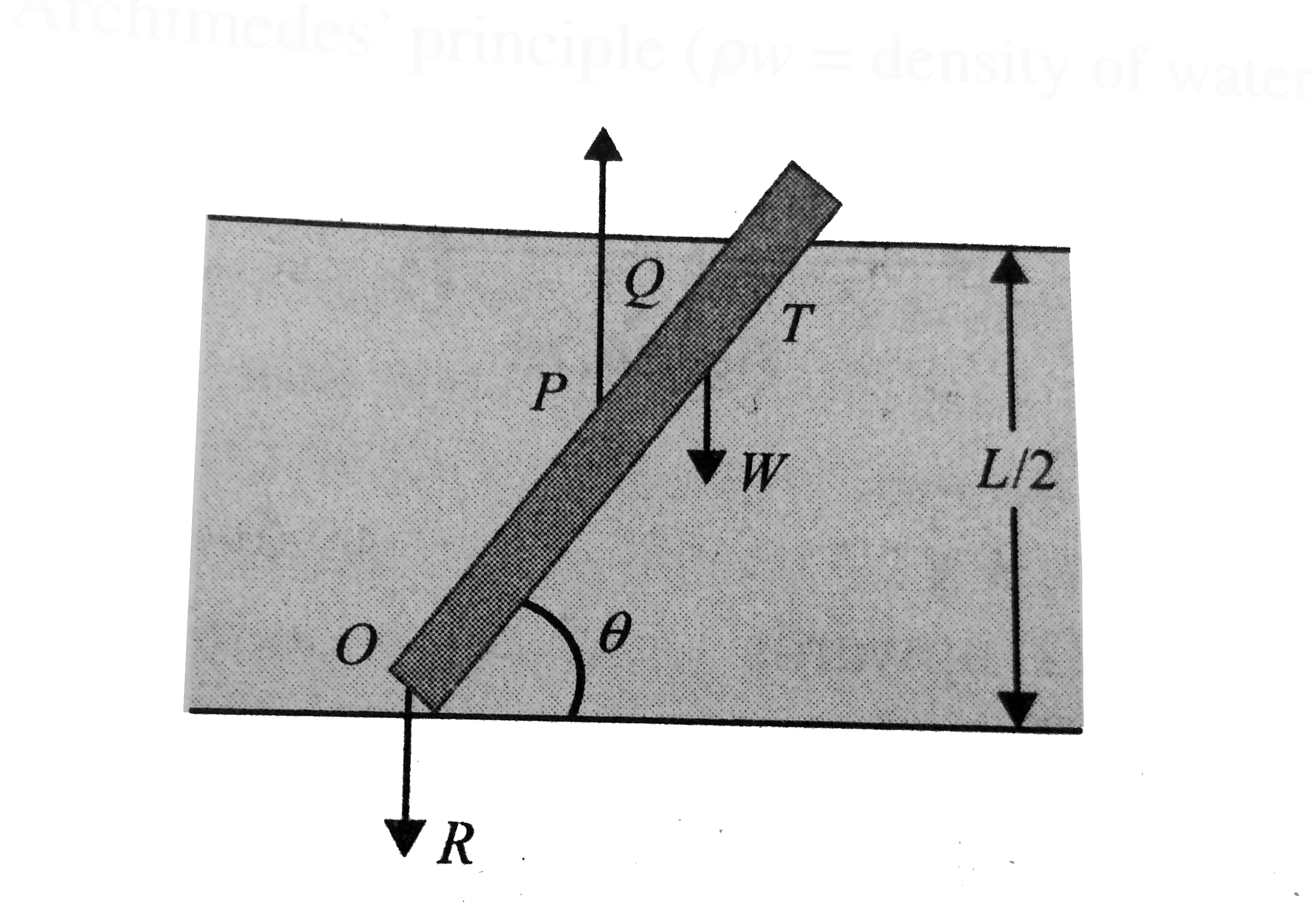
This force acts at $P$ , where $O P = \frac{O T}{2} = \frac{l}{4 sin θ}$
Balancing torque about $O$ is
$W O Q cos θ = B O P cos θ$
$(L A ρ g) \frac{L}{2} = (\frac{L}{sin θ}) A ρ_{w} g (\frac{L}{4 sin θ})$
${sin}^{2} θ = \frac{ρ_{w}}{4 ρ} \Rightarrow {sin}^{2} θ = \frac{1}{2} \Rightarrow θ = 45^{\circ}$
Also balancing forces $R + W = B$
$R = B - W = \frac{ρ A ρ_{w} g}{2 sin θ} - L A ρ g$
$= L A ρ g [\frac{1}{sin θ} - 1]$ ( $∵ ρ_{w} = 2 ρ) = (\sqrt{2} - 1) m g$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-Linked Comprehension

Home
Ask Doubt
Profile