The dimensions of four wires of the same material an given below. In which wire the increase in the length will be maximum?
Length 100cm, diameter 1mm
Length 200cm, diameter 2mm
Length 300cm, diameter 3mm
Length 50cm, diameter 0.5mm
The correct Answer is:D
To determine which wire experiences the maximum increase in length when subjected to the same force, we can use the relationship derived from Young's modulus. The increase in length (ΔL) of a wire is given by the formula:
ΔL=F⋅LA⋅Y
Where:
- F is the force applied,
- L is the original length of the wire,
- A is the cross-sectional area of the wire,
- Y is Young's modulus (which is constant for wires made of the same material).
The cross-sectional area A of a wire with diameter d is given by:
A=π4d2
Substituting this into the equation for ΔL, we get:
ΔL=F⋅Lπ4d2⋅Y
This simplifies to:
ΔL∝Ld2
Thus, the increase in length is directly proportional to the ratio of the original length L to the square of the diameter d2. To find which wire has the maximum increase in length, we need to calculate Ld2 for each wire.
Step-by-Step Calculation:
1. Wire 1:
- Length = 100 cm = 1000 mm
- Diameter = 1 mm
- Ld2=100012=1000
2. Wire 2:
- Length = 200 cm = 2000 mm
- Diameter = 2 mm
- Ld2=200022=20004=500
3. Wire 3:
- Length = 300 cm = 3000 mm
- Diameter = 3 mm
- Ld2=300032=30009≈333.33
4. Wire 4:
- Length = 50 cm = 500 mm
- Diameter = 0.5 mm
- Ld2=500(0.5)2=5000.25=2000
Conclusion:
Comparing the values of Ld2:
- Wire 1: 1000
- Wire 2: 500
- Wire 3: 333.33
- Wire 4: 2000
The maximum value is for Wire 4, which has a value of 2000. Therefore, the wire with the maximum increase in length is Wire 4.
- F is the force applied,
- L is the original length of the wire,
- A is the cross-sectional area of the wire,
- Y is Young's modulus (which is constant for wires made of the same material).
- Length = 100 cm = 1000 mm
- Diameter = 1 mm
- Ld2=100012=1000
- Length = 200 cm = 2000 mm
- Diameter = 2 mm
- Ld2=200022=20004=500
- Length = 300 cm = 3000 mm
- Diameter = 3 mm
- Ld2=300032=30009≈333.33
- Length = 50 cm = 500 mm
- Diameter = 0.5 mm
- Ld2=500(0.5)2=5000.25=2000
Comparing the values of Ld2:
- Wire 1: 1000
- Wire 2: 500
- Wire 3: 333.33
- Wire 4: 2000
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning13videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective16videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
When a certain weight is suspended from a long uniform wire, its length increases by 1cm. If the same weight is suspended from another wire of the same material and length but having a diameter half of the first one, the increases in length will be
View SolutionWhen a certain weight is suspended from a long uniform wire, its length increases by 1cm. If the same weight is suspended from another wire of the same material and length but having a diameter half of the first one, the increases in length will be
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L and radius r is clamped at one end. On stretching the other end of the wire with a force F, the increase in its length is 1. If another wire of same material but of length 2L and radius 2r is stretched with a force 2F, the increase in its leagth will be
Al4Bl2ClD2l
_E01_007_Q01.png)
The load versus elongation graph for four wires of the same material and same length is shown in the figure. The hinnest wire is represented by the lineView SolutionThe load versus extension graph for four wires of same material is shown.
The thinnest wire is represented by the line
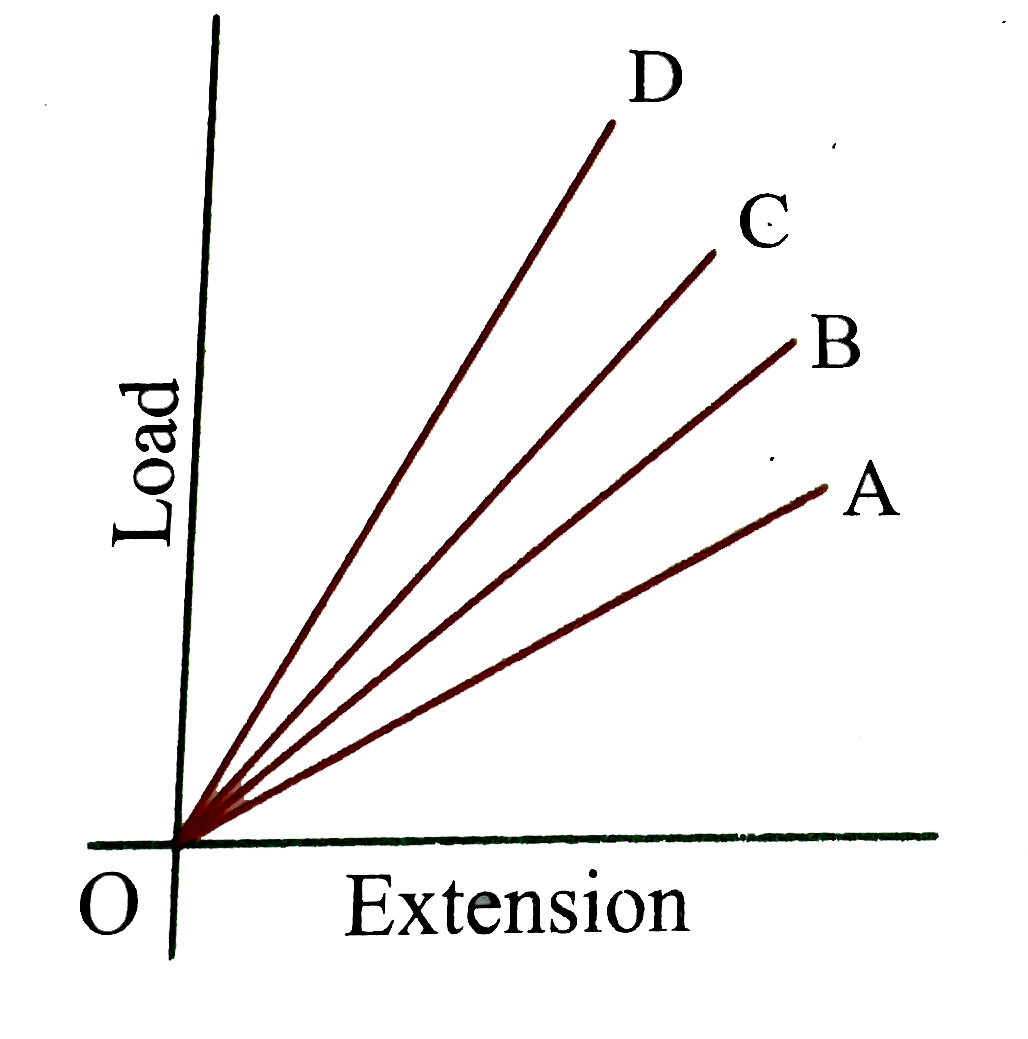 View Solution
View SolutionThe load versus elongation graph for four wires of the same material is shown in the figure. The thickest wire is represented by
 View Solution
View SolutionA wire of length L and radius a rigidlyl fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is L, if another wire of same material but of length 2 L and radius 2 a is stretched with a force 2 F, the increase in its length will be
View SolutionFour wires made of same material have different lengths and radii, the wire having more resistance in the following case is
View SolutionTwo similar sonometer wires of the same material under the same tension produces 3 beats per second. The length of one wire is 40 cm and that of the other is 40.1 cm. Calculate the frequency of the two wires ?
View SolutionThe load versus elongatino graphs for four wires A,B,C and D of the same material and equal lenghts are shown in the figure . The thickest wire is represented by the fine
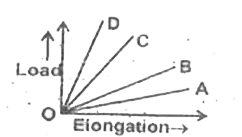 View Solution
View Solution

