A composite rod consists of a steel rod of length 25cm and area 2A and a copper rod of length 50cm and area A. The composite rod is subjected to an axial load F. If the Young's moduli of steel and copper are in the ratio 2:1 then
the extension produced in copper rod will be more
the extension in copper and steel parts will be in the ratio 1:2
the stress applied to copper rod will be more
no extension will be produced in the steel rod
The correct Answer is:A, B, C
To solve the problem, we need to analyze the composite rod made of steel and copper under an axial load F. We will determine the extensions in both rods and compare them.
Given Data:
- Length of steel rod, Ls=25cm=0.25m
- Area of steel rod, As=2A
- Length of copper rod, Lc=50cm=0.50m
- Area of copper rod, Ac=A
- Ratio of Young's moduli, EsEc=21
Step 1: Express Young's Moduli
Let the Young's modulus of copper be Ec. Then, the Young's modulus of steel can be expressed as:
Es=2Ec
Step 2: Calculate Stress in Each Rod
Stress is defined as force per unit area:
- Stress in the steel rod:
σs=FAs=F2A
- Stress in the copper rod:
σc=FAc=FA
Step 3: Relate Strain to Stress and Young's Modulus
Using the relationship ϵ=σE:
- Strain in the steel rod:
ϵs=σsEs=F2A2Ec=F4AEc
- Strain in the copper rod:
ϵc=σcEc=FAEc=FAEc
Step 4: Calculate Extensions
The extension ΔL in each rod can be expressed as:
- Extension in the steel rod:
ΔLs=ϵs⋅Ls=(F4AEc)⋅0.25
ΔLs=F⋅0.254AEc=F16AEc
- Extension in the copper rod:
ΔLc=ϵc⋅Lc=(FAEc)⋅0.50
ΔLc=F⋅0.50AEc=F2AEc
Step 5: Compare Extensions
Now, we can find the ratio of the extensions:
ΔLsΔLc=F16AEcF2AEc=1/161/2=18
This implies:
ΔLc=8ΔLs
Conclusion
The extension produced in the copper rod is greater than that in the steel rod. Thus, the correct answer is that the extension produced in the copper rod will be more.
- Length of steel rod, Ls=25cm=0.25m
- Area of steel rod, As=2A
- Length of copper rod, Lc=50cm=0.50m
- Area of copper rod, Ac=A
- Ratio of Young's moduli, EsEc=21
Let the Young's modulus of copper be Ec. Then, the Young's modulus of steel can be expressed as:
Es=2Ec
Stress is defined as force per unit area:
- Stress in the steel rod:
σs=FAs=F2A
- Stress in the copper rod:
σc=FAc=FA
Using the relationship ϵ=σE:
- Strain in the steel rod:
ϵs=σsEs=F2A2Ec=F4AEc
- Strain in the copper rod:
ϵc=σcEc=FAEc=FAEc
The extension ΔL in each rod can be expressed as:
- Extension in the steel rod:
ΔLs=ϵs⋅Ls=(F4AEc)⋅0.25
ΔLs=F⋅0.254AEc=F16AEc
- Extension in the copper rod:
ΔLc=ϵc⋅Lc=(FAEc)⋅0.50
ΔLc=F⋅0.50AEc=F2AEc
Now, we can find the ratio of the extensions:
ΔLsΔLc=F16AEcF2AEc=1/161/2=18
This implies:
ΔLc=8ΔLs
The extension produced in the copper rod is greater than that in the steel rod. Thus, the correct answer is that the extension produced in the copper rod will be more.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning13videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective16videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
A brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2View SolutionA composite wire of uniform diameter 3mm consisting of copper wire of length 2.2 m and a steel wire of length 1. 6m stretches under a load by 0.7mm. Calcualte the load, given that the Young's modulus of copper is 1.1×1011Pa and for steel is 2.0×1011Pa.
View SolutionA composite rod of mass 2m and length 2l comprises two indentica rods joined end to end at P. The composite rod hinged at one of its ends is kept horizontal as shown in the figure. If it is realeased from rest.
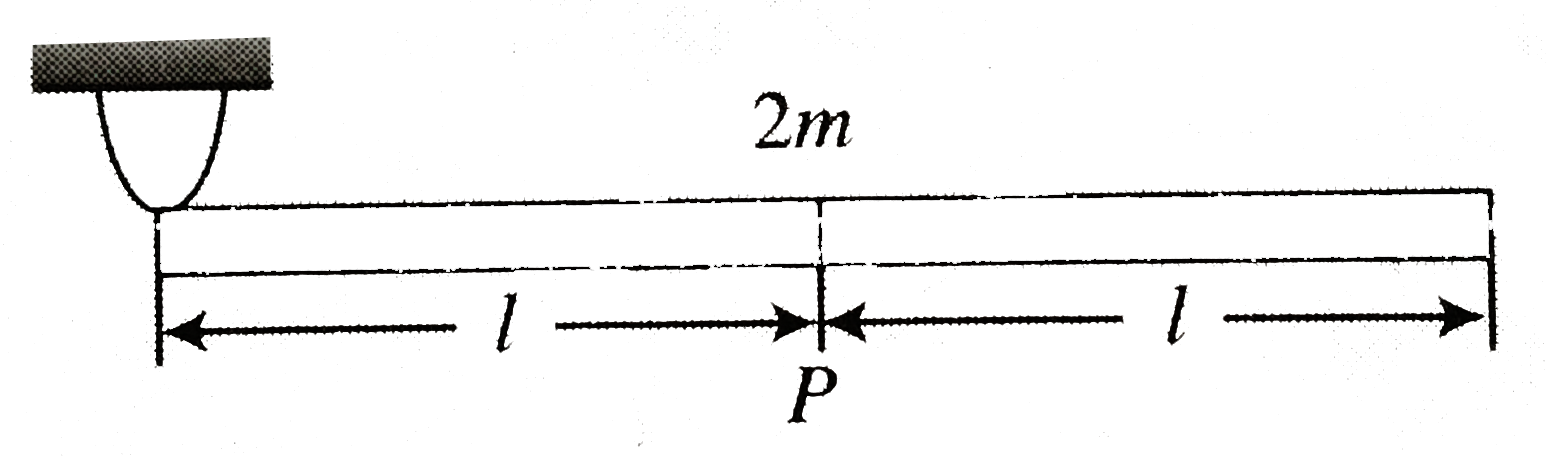
a. find its angular speed when it becomes vertical.
b. If the lower rod gets detached with the upper rod due to centrifugal effect at their joint P, at the vertical position of the composite rod, find their linear and angular velocities just after their separation.View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composite rod increases by 1.91mm. When the composite rod is prevented from expanding by holding it between two rigid walls, it is found that the constituent rods have remained unchanged in length inspite of rise of temperature. Find young's modulus and the coefficient of linear expansion of the second rod (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA copper rod with length 1.4 m and area of cross-section of 2cm2 is fastened to a steel rod with length L and cross-sectional area 1cm2. The compound rod is subjected to equal and opposite pulls to magnitude 6.00×104 N at its ends .
(a) Find the length L of the steel rod if the elongation of the two rods are equal .
(b) What is stress in each rod ?
(c ) What is the strain in each rod ? [Ysteel=2×1011Pa,YCu=1.1×1011Pa]
 View Solution
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .
 View Solution
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1.∘C−1 and that of steel =46Wm−1.∘C−1 .
 View Solution
View SolutionA uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composte rod increases by 1.91mm. When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
View Solution

