A substance breaks down under a stress of . If the density of the wire is , find the minimum length of the wire which will break under its own weight .
The correct Answer is:5
To find the minimum length of the wire that will break under its own weight, we can follow these steps:
1. Understanding Breaking Stress:
The breaking stress (σ) is defined as the force (weight in this case) per unit area (A) that a material can withstand before failing. The formula for breaking stress is given by:
σ=FA
where F is the weight of the wire.
2. Weight of the Wire:
The weight (W) of the wire can be expressed as:
W=mg
where m is the mass of the wire and g is the acceleration due to gravity.
3. Mass of the Wire:
The mass of the wire can be calculated using its volume (V) and density (ρ):
m=V⋅ρ
The volume of the wire can be expressed as:
V=A⋅L
where L is the length of the wire.
4. Substituting Volume into Mass:
Therefore, the mass can be rewritten as:
m=A⋅L⋅ρ
5. Substituting Mass into Weight:
Now substituting this expression for mass into the weight formula:
W=(A⋅L⋅ρ)⋅g
6. Substituting Weight into Breaking Stress:
Now we can substitute the expression for weight into the breaking stress formula:
σ=(A⋅L⋅ρ⋅g)A
The area A cancels out:
σ=L⋅ρ⋅g
7. Setting Up the Equation:
According to the problem, the breaking stress is given as 105 Pa. Therefore, we can set up the equation:
105=L⋅ρ⋅g
8. Solving for Length (L):
Rearranging the equation to find L:
L=105ρ⋅g
9. Substituting Values:
Now substituting the given values: ρ=2×103kg/m3 and g=10m/s2:
L=105(2×103)⋅10
10. Calculating Length:
Simplifying the expression:
L=1052×104=1052×104=102=5m
Final Answer:
The minimum length of the wire which will break under its own weight is 5 meters.
The breaking stress (σ) is defined as the force (weight in this case) per unit area (A) that a material can withstand before failing. The formula for breaking stress is given by:
σ=FA
where F is the weight of the wire.
The weight (W) of the wire can be expressed as:
W=mg
where m is the mass of the wire and g is the acceleration due to gravity.
The mass of the wire can be calculated using its volume (V) and density (ρ):
m=V⋅ρ
The volume of the wire can be expressed as:
V=A⋅L
where L is the length of the wire.
Therefore, the mass can be rewritten as:
m=A⋅L⋅ρ
Now substituting this expression for mass into the weight formula:
W=(A⋅L⋅ρ)⋅g
Now we can substitute the expression for weight into the breaking stress formula:
σ=(A⋅L⋅ρ⋅g)A
The area A cancels out:
σ=L⋅ρ⋅g
According to the problem, the breaking stress is given as 105 Pa. Therefore, we can set up the equation:
105=L⋅ρ⋅g
Rearranging the equation to find L:
L=105ρ⋅g
Now substituting the given values: ρ=2×103kg/m3 and g=10m/s2:
L=105(2×103)⋅10
Simplifying the expression:
L=1052×104=1052×104=102=5m
The minimum length of the wire which will break under its own weight is 5 meters.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks
1 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - SCQ_TYPE
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Linked Comprehension
30 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A substance breaks down under a stress of 105 Pa. If the density of the substance is 2×103kgm3, find the minimum length of the wire made of this substance which will break under its own weight (g=10ms2)
View SolutionA material beaks up under a stress of 20×105N/m2. If the density of the material is 2.5×103kg/m3, calculate the length of a wire made of this material, which on hanging may break under its own weight. (g=9.8m/s2)
View SolutionA stress of 106N/m2 is required for breaking a material. If the density of the material is 3×103Kg/m3, then what should be the minimum length of the wire made of the same material so that it breaks by its own weight (g=10m/s2)
View SolutionThe breaking stress of steel is 7.85×108N/m2 and density of steel is 7.7×103kg/m3. The maximum frequency to which a string 1m long can be tuned is
View SolutionThe breaking stress for a metal is 9×1010Nm−2 The density of the metal is 9000kgm−3 . If g=10Nkg−1 , the maximum length of the wire made of this metal which may be suspended without breaking is 10k m . Find the value of k.
View SolutionThe breaking stress of a material is 108Nm−2. Find the greatest length of a wire that could hang vertically without breaking? Density of material =3000kgm−3.
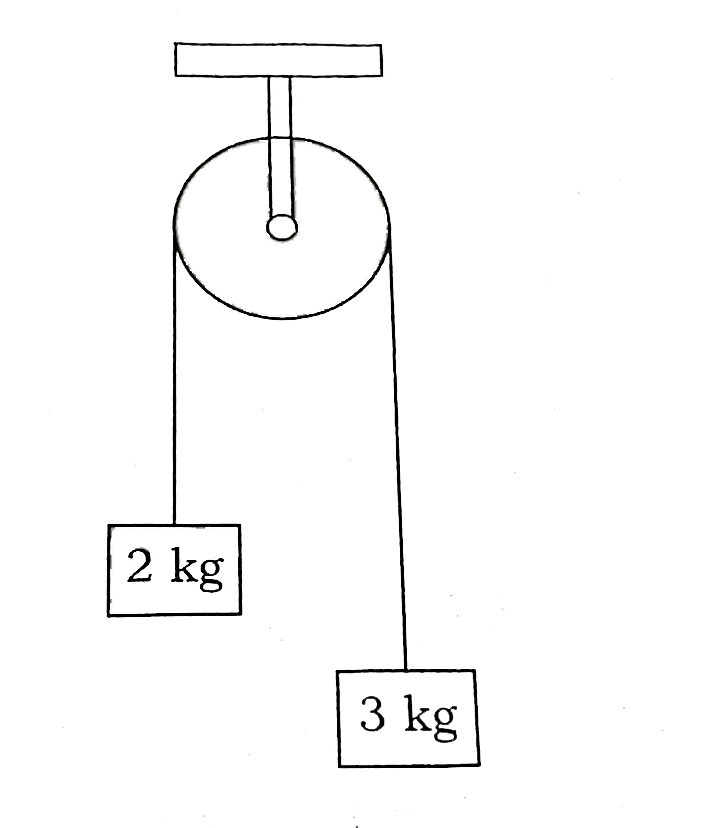
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
View SolutionA lift of mass 1000 kg is suspended by steel wire of maximum safe stress 1.4×108N/m2. Find the minimum diameter of the wire, if the maximum acceleration of the lift is 1.2ms−2
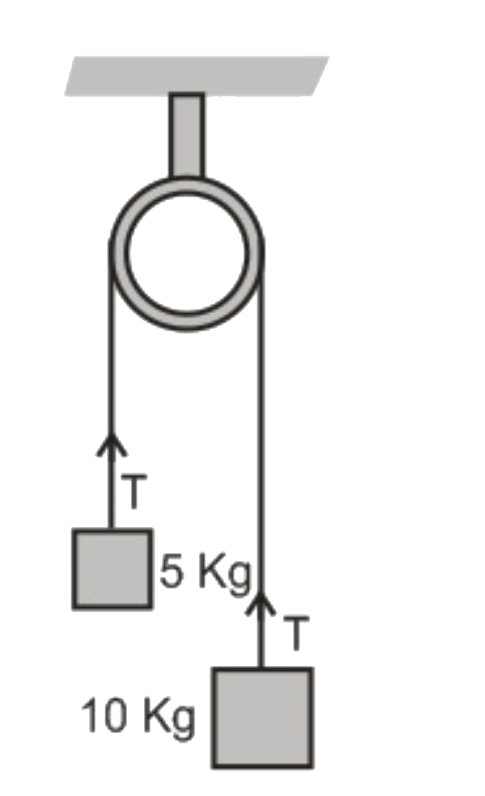
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
View SolutionBreaking stress for a material is 2×108N/m2. What maximum length of the wire of this material can be taken t the wire does not break by own weight? Density of material = 5×103kg/m3
View Solution
