A lift of mass 1000 kg is suspended by steel wire of maximum safe stress 1.4×108N/m2. Find the minimum diameter of the wire, if the maximum acceleration of the lift is 1.2ms−2
The correct Answer is:0.01m
To solve the problem, we need to find the minimum diameter of the steel wire that can safely support a lift with a mass of 1000 kg while considering the maximum acceleration of the lift. Here are the steps to arrive at the solution:
Step 1: Calculate the weight of the lift.
The weight (W) of the lift can be calculated using the formula:
W=m⋅g
where:
- m=1000kg (mass of the lift)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the weight:
W=1000kg⋅9.8m/s2=9800N
Step 2: Calculate the maximum tension in the wire.
The maximum tension (T) in the wire occurs when the lift is accelerating upwards. The formula for tension when considering acceleration is:
T=W+m⋅a
where:
- a=1.2m/s2 (maximum acceleration of the lift)
Calculating the maximum tension:
T=9800N+(1000kg⋅1.2m/s2)
T=9800N+1200N=11000N
Step 3: Use the maximum safe stress to find the minimum cross-sectional area.
The maximum safe stress (σ) is given as:
σ=1.4×108N/m2
The formula relating stress, force, and area is:
σ=TA
where A is the cross-sectional area of the wire.
Rearranging the formula to find the area:
A=Tσ
Substituting the values:
A=11000N1.4×108N/m2
A=7.857×10−5m2
Step 4: Calculate the radius of the wire.
The area of a circle is given by:
A=πr2
Rearranging to find the radius (r):
r=√Aπ
Substituting the area:
r=√7.857×10−5m2π
r≈√7.857×10−53.14159
r≈√2.5×10−5
r≈0.005m
Step 5: Calculate the diameter of the wire.
The diameter (d) is twice the radius:
d=2r
d=2×0.005m=0.01m
Final Answer:
The minimum diameter of the wire is:
0.01m
---
The weight (W) of the lift can be calculated using the formula:
W=m⋅g
where:
- m=1000kg (mass of the lift)
- g=9.8m/s2 (acceleration due to gravity)
W=1000kg⋅9.8m/s2=9800N
The maximum tension (T) in the wire occurs when the lift is accelerating upwards. The formula for tension when considering acceleration is:
T=W+m⋅a
where:
- a=1.2m/s2 (maximum acceleration of the lift)
T=9800N+(1000kg⋅1.2m/s2)
T=9800N+1200N=11000N
The maximum safe stress (σ) is given as:
σ=1.4×108N/m2
σ=TA
where A is the cross-sectional area of the wire.
A=Tσ
A=11000N1.4×108N/m2
A=7.857×10−5m2
The area of a circle is given by:
A=πr2
Rearranging to find the radius (r):
r=√Aπ
r=√7.857×10−5m2π
r≈√7.857×10−53.14159
r≈√2.5×10−5
r≈0.005m
The diameter (d) is twice the radius:
d=2r
d=2×0.005m=0.01m
The minimum diameter of the wire is:
0.01m
Similar Questions
A bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View Solution
Knowledge Check
A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms2 (ii) lowered with an acceleration of 4.9ms−2. The ratio of tension in the first and second case is
A3:1B1:2C1:3D2:1
A bob of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. Then area of cross-section of the wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionIf the elastic limit of copper is 1.5×108N/m2,determine the minimum diameter a copper wire can have under a load of10.0kg force , if its elastic limit is not to be exceeded.
View SolutionA substance breaks down under a stress of 105Pa. If the density of the wire is 2×103kg/m3, find the minimum length of the wire which will break under its own weight (g=10ms−12).
View SolutionThe maximum stress that can be applied to the material of a wire used to suspend an elevator is 1.3×108Nm−2. If the mass of the elevator is 900 kg and it moves up with an acceleration of 2.2ms−2 , what is the minimum diameter of the wire?
View SolutionA disc of mass 1 kg and radius 10 cm is suspended by vertical wire at its centre. If the time period is 3.2 s. Find the modulus of torison.
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
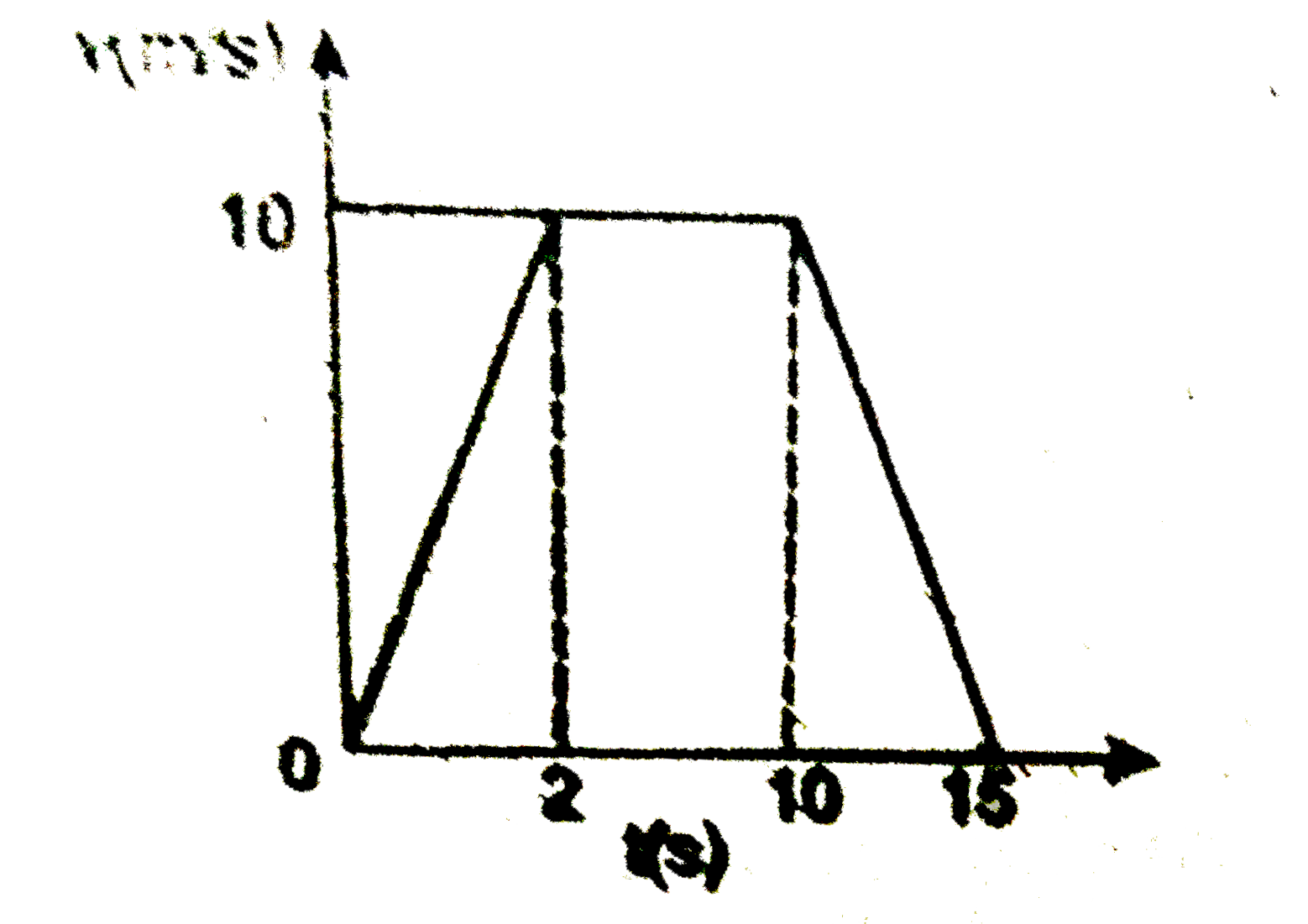
View Solution
