Assertion: Kepler's second law can be understood by conservation of angular momentum principle.
Reason: Kepler's second law is related with areal velocity which can further be proved to be used on coservation of angular momentum as (dA/dt)=(r2ω)/2.
Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:A
To solve the given question, we need to analyze the assertion and the reason provided:
Assertion: Kepler's second law can be understood by the conservation of angular momentum principle.
Reason: Kepler's second law is related to areal velocity, which can further be proved to be used on conservation of angular momentum as dAdt=r2ω2.
1. Understanding Kepler's Second Law:
- Kepler's second law, also known as the law of areas, states that a line segment joining a planet to the Sun sweeps out equal areas during equal intervals of time. This implies that the areal velocity (area swept per unit time) is constant.
2. Areal Velocity:
- The areal velocity dAdt can be expressed in terms of the radius r and the angular velocity ω. The area A swept out by the radius vector in a small time interval dt can be approximated as:
dA=12r2dθ
- Therefore, the areal velocity is given by:
dAdt=12r2dθdt=12r2ω
3. Conservation of Angular Momentum:
- Angular momentum L for a planet moving in an orbit is given by:
L=mvr=mr2ω
- Since there are no external torques acting on the planet, the angular momentum is conserved:
L=constant
- This means that mr2ω remains constant, which implies that the product r2ω is also constant for a given mass m.
4. Connecting Kepler's Second Law and Angular Momentum:
- From the expression for areal velocity, we see that:
dAdt=12r2ω
- Since r2ω is constant (due to conservation of angular momentum), it follows that dAdt is also constant. This directly supports Kepler's second law.
5. Conclusion:
- Both the assertion and reason are true. The assertion that Kepler's second law can be understood through the conservation of angular momentum is valid, and the reason provides a correct explanation of this relationship.
Final Answer:
Thus, the answer is that both statements are true, and the reason is the correct explanation of the assertion.
- Kepler's second law, also known as the law of areas, states that a line segment joining a planet to the Sun sweeps out equal areas during equal intervals of time. This implies that the areal velocity (area swept per unit time) is constant.
- The areal velocity dAdt can be expressed in terms of the radius r and the angular velocity ω. The area A swept out by the radius vector in a small time interval dt can be approximated as:
dA=12r2dθ
- Therefore, the areal velocity is given by:
dAdt=12r2dθdt=12r2ω
- Angular momentum L for a planet moving in an orbit is given by:
L=mvr=mr2ω
- Since there are no external torques acting on the planet, the angular momentum is conserved:
L=constant
- This means that mr2ω remains constant, which implies that the product r2ω is also constant for a given mass m.
- From the expression for areal velocity, we see that:
dAdt=12r2ω
- Since r2ω is constant (due to conservation of angular momentum), it follows that dAdt is also constant. This directly supports Kepler's second law.
- Both the assertion and reason are true. The assertion that Kepler's second law can be understood through the conservation of angular momentum is valid, and the reason provides a correct explanation of this relationship.
Thus, the answer is that both statements are true, and the reason is the correct explanation of the assertion.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning13videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension23videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Single Correct122videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion : The total momentum of an isolated system of particles is conserved.
Reason: The law of conservation of momentum follows from the second and third law of motion.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is the not correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false. - Question 2 - Select One
The angular momentum of an electron in a given stationary state can be expressed as mevr=nh2π. Based on this expression an electron can move only in those orbits for which its angular momentum is
Aequal to nBintegral multiple of h2πCmultiple of nDequal to h2π only.
Statement-1: Kepler's law of areas is equivalent to the law of conservation of angular momentum
Statement-2: Areal velocity dAdt=L2m= constantView SolutionSTATEMENT -1 : Kepler's second law is the consequence of law of conservation of angular momentum.
STATEMENT -2 : In planetary motion, the momentum, angular momentum and mechanical energy is conserved.
STATEMENT -3 : The gravitational field of a circular ring is maximum at a point upon axis at distance R√2 from the centre, where R is the radius of ring.View SolutionLaws of conservation of linear and angular momentum can be derived from Newton's laws of motion in mechanics. Are they valid beyond mechanics?
View SolutionAssertion : Motional induced emf e=Bvl can be derived from the relation e=−dϕdt
Reason : Lenz's law is a consequence of law of conservation of energy.View SolutionAssertion : Areal velocity of a planet around of surface area and density is same for two planets, escape velocities will be same for both
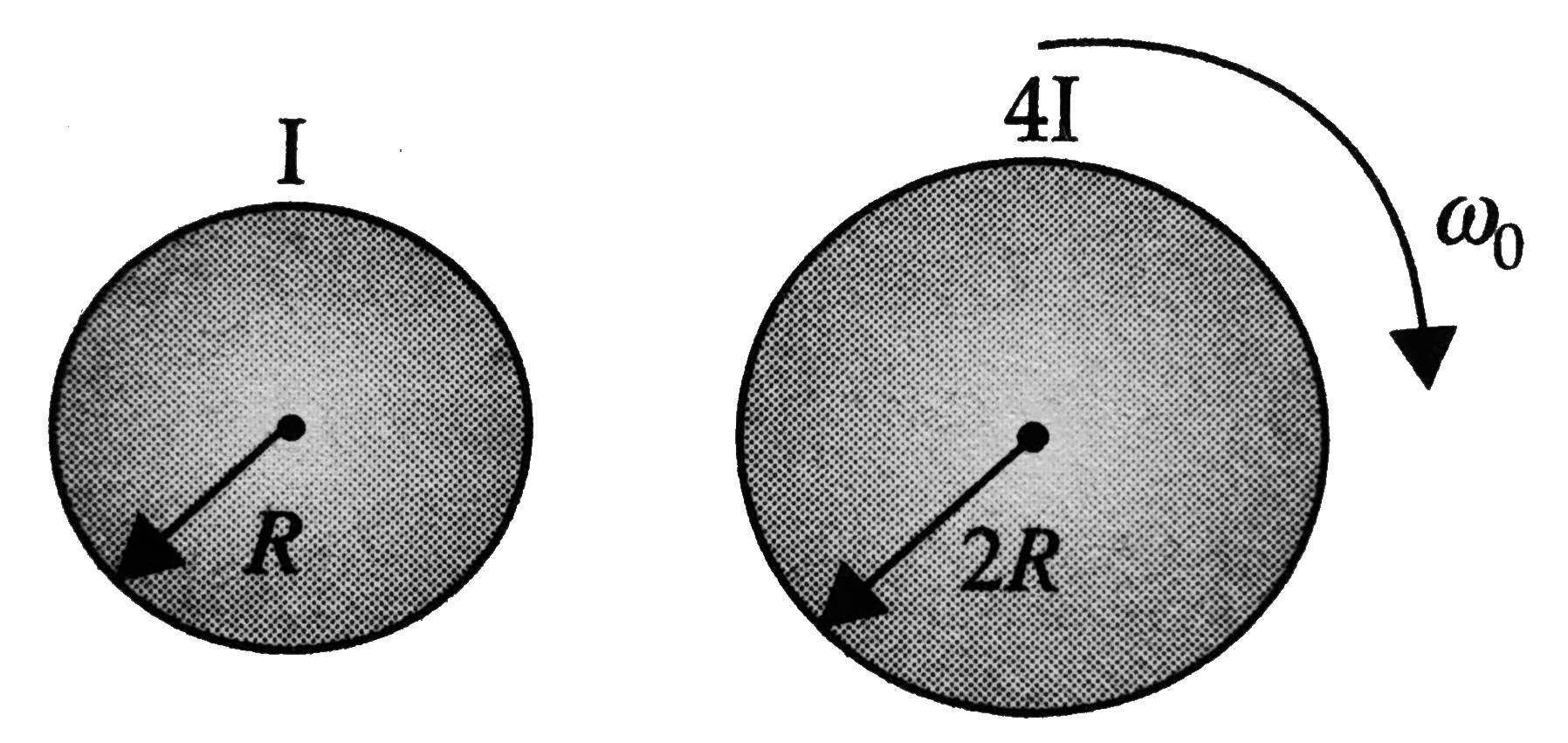
Reason : Areal velocity =L2m, Where L is angular momentum of planet about centre of sun.View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
 View Solution
View Solution

