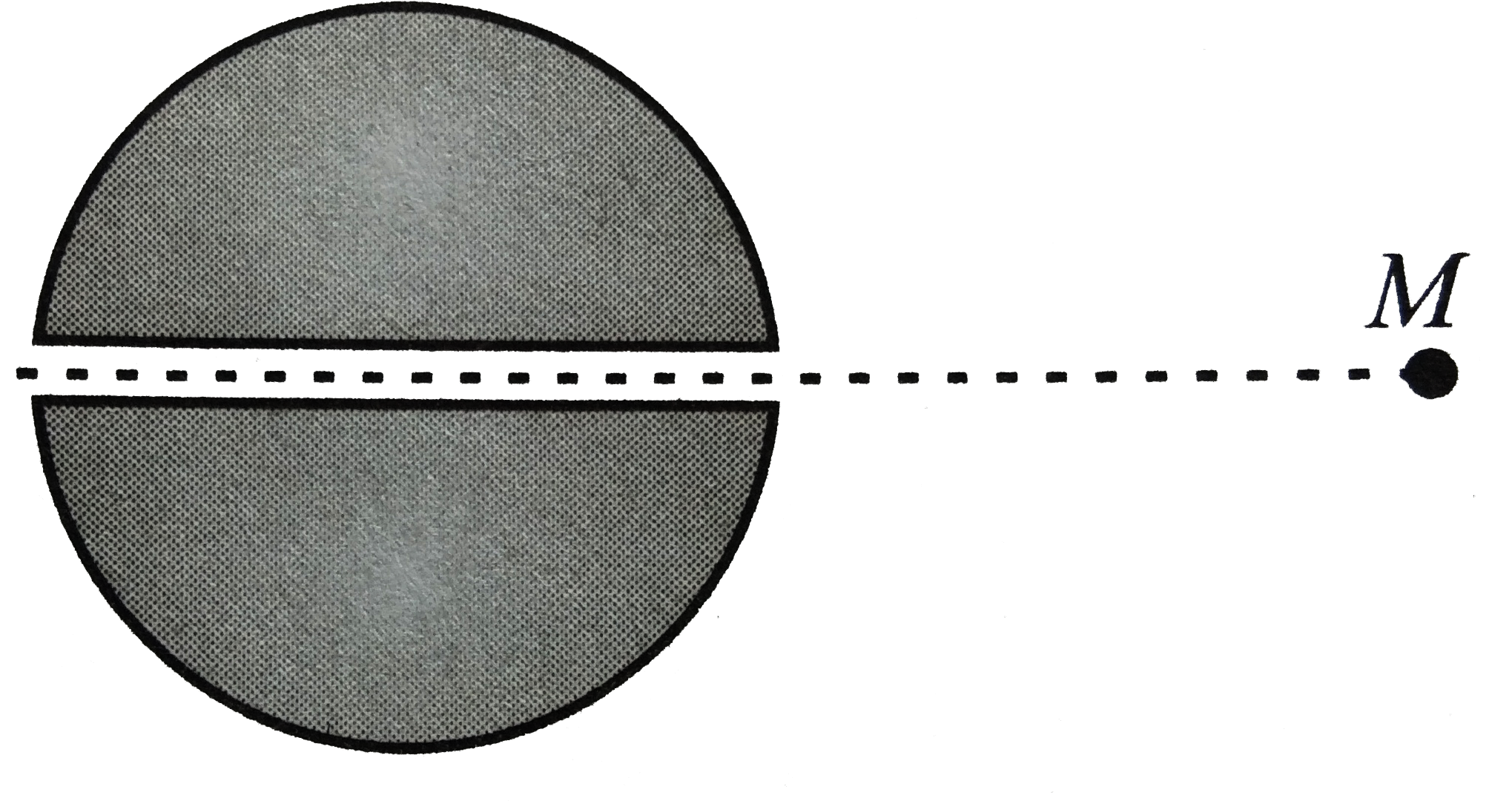
Statement I: In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum.
Statement II: When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing.
Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:A
Till particle reaches the centre of the planet, force on both the bodies are in direction on increasing. After the particle crosses the centre of the planet, forces on both are retarding in nature. Hence as the particle passes through the centre of the planet, sum of kinetic energies of oth the bodies is maximum. Therefore Statement 1 is true, Statement 2 is true: Statement 2 is a correct explanation for Statement 1.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension
23 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionFour particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionAssertion: Two spherical bodies of mass ratio 1:2 travel towards each other (starting from rest) under the action of their mutual gravitational attraction. Then, the ratio of their kinetic energies at any instant is 2:1
Reason: At any instant their momenta are same.
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View Solution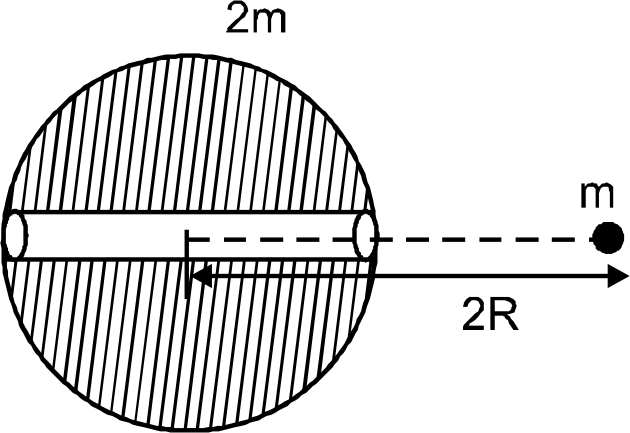
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)
View Solution
