Find the force on a charge q1(=20μC) due to the charge of q2(=10μC) if the positions of the charges are given as P1(1,−1,2) and Q(−1,1,1)
To find the force on charge q1 due to charge q2, we can use Coulomb's Law, which states that the force F between two point charges is given by:
F=k|q1q2|r2^r
where:
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges,
- ^r is the unit vector pointing from one charge to the other.
Step 1: Identify the charges and their positions
Given:
- q1=20μC=20×10−6C
- q2=10μC=10×10−6C
- Position of P1(1,−1,2) for q1
- Position of Q(−1,1,1) for q2
Step 2: Calculate the position vectors
Let:
- r1=(1,−1,2)
- r2=(−1,1,1)
Step 3: Find the vector from q2 to q1
The vector r21 from q2 to q1 is given by:
r21=r1−r2=(1−(−1),−1−1,2−1)=(2,−2,1)
Step 4: Calculate the magnitude of r21
The magnitude r is calculated as:
r=|r21|=√(2)2+(−2)2+(1)2=√4+4+1=√9=3
Step 5: Calculate the unit vector ^r
The unit vector ^r is given by:
^r=r21|r21|=(2,−2,1)3=(23,−23,13)
Step 6: Apply Coulomb's Law
Now, we can substitute the values into Coulomb's Law:
F=k|q1q2|r2^r
Substituting the values:
F=9×109(20×10−6)(10×10−6)(3)2(23,−23,13)
Calculating the force:
F=9×109200×10−129(23,−23,13)
=9×109×2009×10−12(23,−23,13)
=2×109×10−12(23,−23,13)
=0.067(23,−23,13)
Final Result
Thus, the force on charge q1 due to charge q2 is:
F=0.067(23,−23,13)N
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges,
- ^r is the unit vector pointing from one charge to the other.
Given:
- q1=20μC=20×10−6C
- q2=10μC=10×10−6C
- Position of P1(1,−1,2) for q1
- Position of Q(−1,1,1) for q2
Let:
- r1=(1,−1,2)
- r2=(−1,1,1)
The vector r21 from q2 to q1 is given by:
The magnitude r is calculated as:
The unit vector ^r is given by:
Now, we can substitute the values into Coulomb's Law:
Thus, the force on charge q1 due to charge q2 is:
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type15videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective32videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples10videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
The given figure gives electric line of force due to two charges q1 and q2. What are the signs of the two charges ?
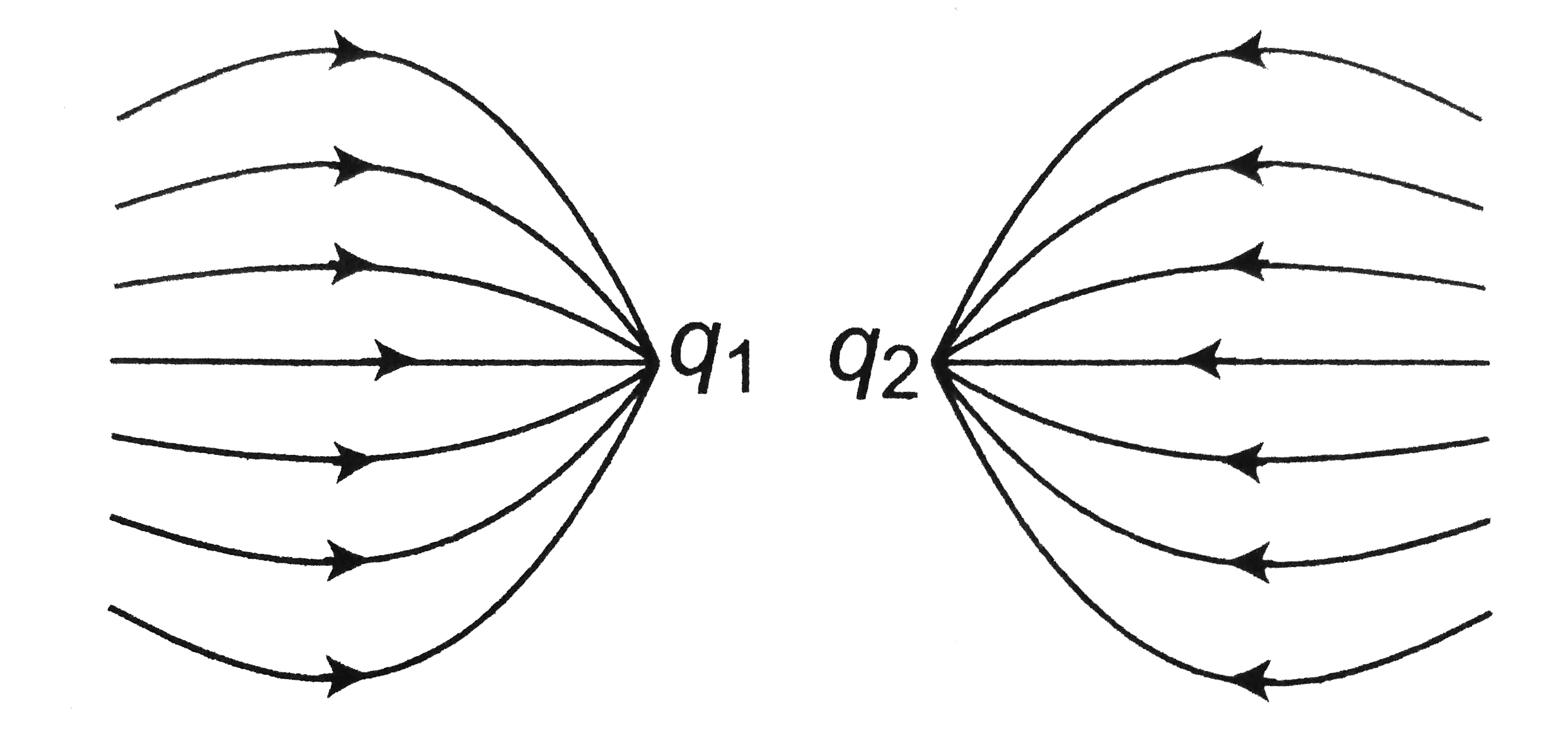 View Solution
View SolutionThe figure shown is a plot of electric field lines due to two charges Q1 and Q2 . The sign of charges is
 View Solution
View SolutionThree concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
View SolutionTwo capacitors of equal capacitance (C1=C2) are as shown in the figure. Initially, while the swithc is open (as shown) one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometime after the switch is closed, the capacitors C1andC2 carry charged Q1andQ2 respectively, the energy stored in the capacitors are U1andU2 respectively. Which of the following expression is correct?
 View Solution
View SolutionThe electric force on a charge q1 due to q2 is (4ˆi−3ˆj)N. What is the force on q2 due to q1
View SolutionA charge q1=2.00μC is located at the origin , and a charge q2=−6.00μC is located at (0,3.00)m.
(a) Find the total electric potential due to these charges at the point P hose coordinates are ( 4.00,0) m .
( b) Find the change in potential energy of the system of two charges plus a charge q3=3.00μC as the latter charge moves from infinity to point P .View SolutionIdentify the correct statement about the charges q1 and q2 then
 View Solution
View SolutionA charge q1 exerts some force on a second charge q2 If a third charge q3 is brought near q2, then the force exterted by q1 on q2
View SolutionThe figure is a plot of lines of force due to two charges q1andq2. Find out the sign of charges.
 View Solution
View SolutionThree charges q1=1μC,q2=−2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q1.
How to proceed Charge q2 will attract charge q1 (along the line joining them) and charge q3 will repel charge q1. Therefore, two forces will act on q1, one due to q2 and another due to q3. Since , the force is a vector quantity both of these force (say F1 and F2) will be added by vector method. Following are two methods of their addition
 View Solution
View Solution

