A charge exerts some force on a second charge If a third charge is brought near , then the force exterted by on
decrease
increase
remains the same
increase, if is of same sign as and decrease, if is of opposite sign as
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on charge q2 due to charges q1 and q3.
1. Understanding the Initial Force:
The force exerted by charge q1 on charge q2 is given by Coulomb's Law:
F12=k⋅|q1⋅q2|r2
where k=14πϵ0 is Coulomb's constant, and r is the distance between q1 and q2.
Hint: Recall that the force between two charges is dependent on the product of their magnitudes and inversely proportional to the square of the distance between them.
2. Introducing a Third Charge:
When a third charge q3 is brought near q2, it will exert a force on q2 as well. The force exerted by q3 on q2 can be expressed as:
F32=k⋅|q3⋅q2|d2
where d is the distance between q3 and q2.
Hint: Remember that the force exerted by q3 on q2 depends on the magnitude of q3 and its distance from q2.
3. Net Force on q2:
The net force acting on q2 is the vector sum of the forces due to q1 and q3:
Fnet=F12+F32
This indicates that the net force on q2 will change due to the presence of q3.
Hint: Consider that the net force is the sum of all forces acting on a charge, and it can change even if one of the forces remains constant.
4. Effect of q3 on F12:
It is important to note that the introduction of q3 does not affect the force F12 (the force between q1 and q2). The force F12 remains:
F12=k⋅|q1⋅q2|r2
unchanged, regardless of the presence of q3.
Hint: The force between two charges is only influenced by those two charges and their distance; other charges nearby do not alter this specific interaction.
5. Conclusion:
Therefore, the force exerted by q1 on q2 remains the same even after bringing q3 near q2.
Final Answer: The force exerted by q1 on q2 remains the same.
The force exerted by charge q1 on charge q2 is given by Coulomb's Law:
F12=k⋅|q1⋅q2|r2
where k=14πϵ0 is Coulomb's constant, and r is the distance between q1 and q2.
When a third charge q3 is brought near q2, it will exert a force on q2 as well. The force exerted by q3 on q2 can be expressed as:
F32=k⋅|q3⋅q2|d2
where d is the distance between q3 and q2.
The net force acting on q2 is the vector sum of the forces due to q1 and q3:
Fnet=F12+F32
This indicates that the net force on q2 will change due to the presence of q3.
It is important to note that the introduction of q3 does not affect the force F12 (the force between q1 and q2). The force F12 remains:
F12=k⋅|q1⋅q2|r2
unchanged, regardless of the presence of q3.
Therefore, the force exerted by q1 on q2 remains the same even after bringing q3 near q2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.3
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Three charges q1=1μC,q2=−2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q1.
How to proceed Charge q2 will attract charge q1 (along the line joining them) and charge q3 will repel charge q1. Therefore, two forces will act on q1, one due to q2 and another due to q3. Since , the force is a vector quantity both of these force (say F1 and F2) will be added by vector method. Following are two methods of their addition

View SolutionA fixed circle of radius a and cnetre O is drawn anda charge +q1 is placed at a distance (3a4) from O on a line through O and perpendicular to plane of circle. And a second charge q2 is similarly placed at a distance 5a12 on the opposite side of circle.
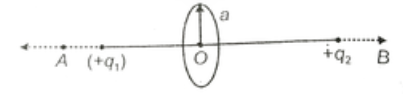
If the values of q1 and q2 are +q,−2q respectively now a third charge −q has to be placed on line AB so that is can be stable equilibrium .The distance of point where third charge is placed from charge q, wouldbe ( take a=12cm).
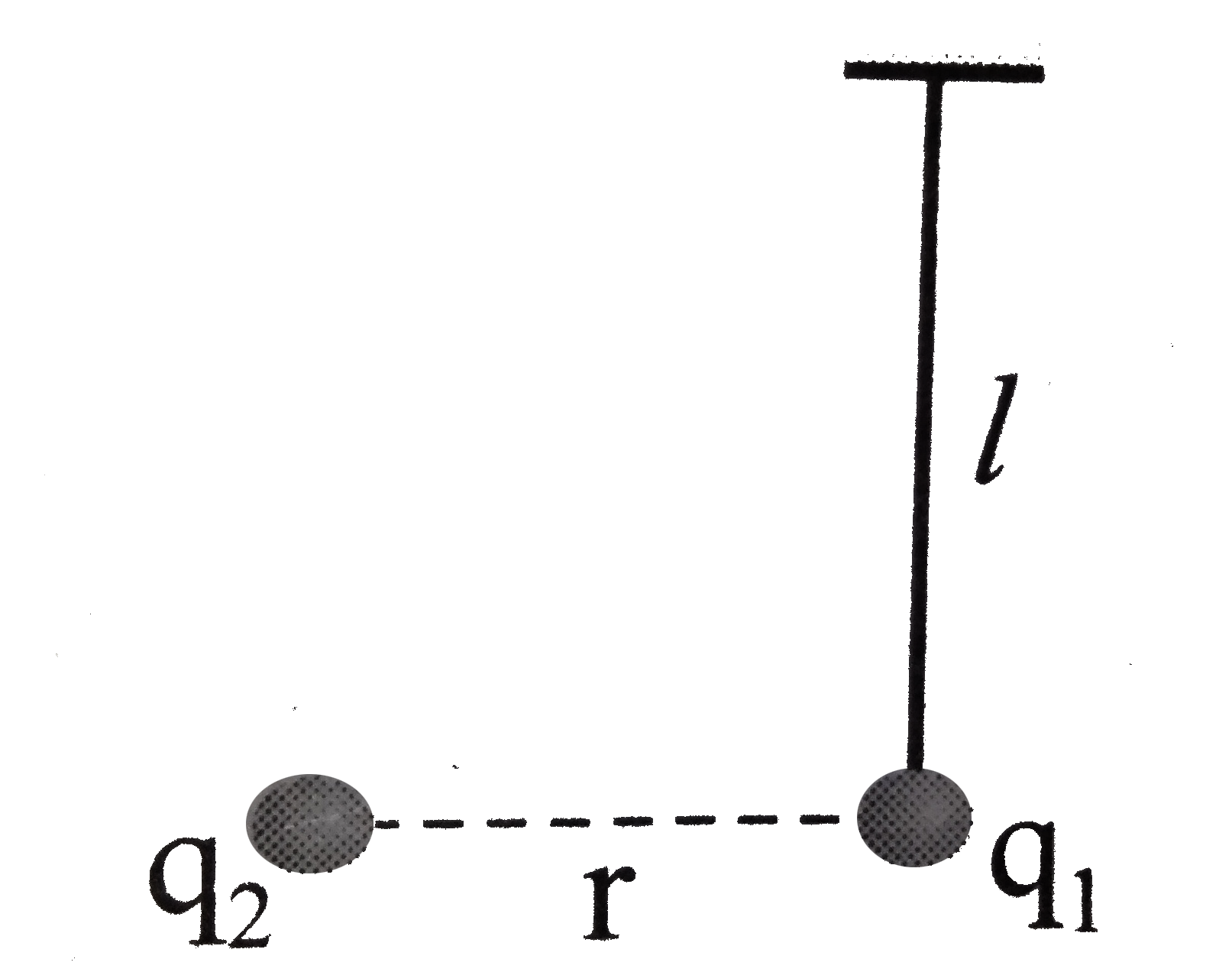
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionFind the force on a charge q1(=20μC) due to the charge of q2(=10μC) if the positions of the charges are given as P1(1,−1,2) and Q(−1,1,1)
View SolutionAn electric charged q exerts a force F on a similar electric charge q swparated by a distance r. A third charge q/4 is placed midway between the two charges. Now the force F will
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1
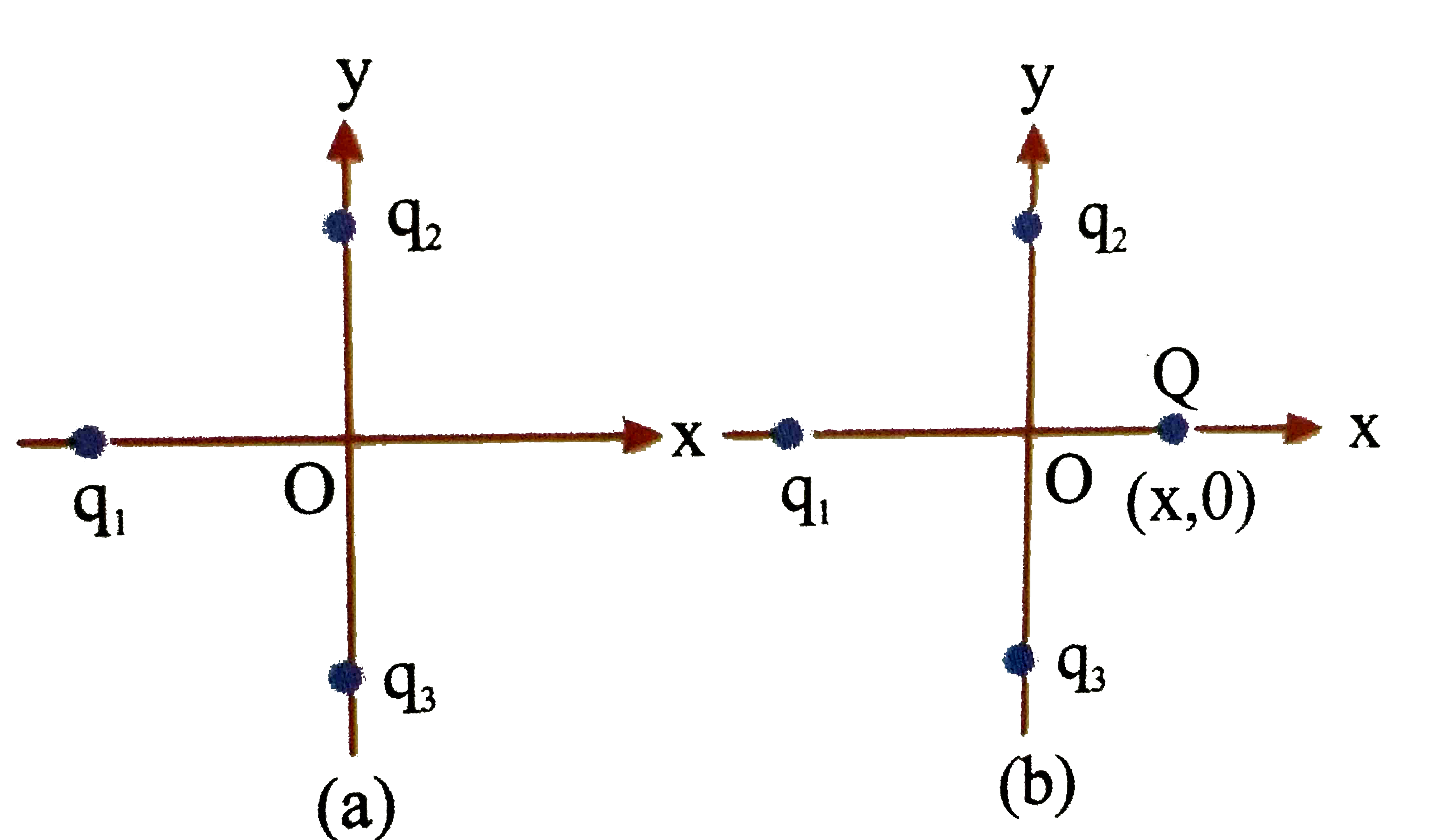
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1

View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1

View SolutionA charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
View Solution
