A point charge Q1=−125μC is fixed at the center of an insulated disc of mass 1 kg. The disc rests on a rough horizontal plane. Another charge Q2=125μC is fixed verically above the center of the disc at a height h=1m. After the disc is displaced slightly in the horizontall direction (friction is sufficient to prevent slipping), find the period of oscillation of disc.

The correct Answer is:2π(hQ)√(6πε0Mh).
Let the radius of the disc be R. If the disc is displaced x, The corresponding angular dispalcement θ=x/R.
The restoring torque τ about the point of contact of disc with ground.
τp=(Fsinθ)R
(Fsinθ)R=1α=[(MR)22+MR2]α
where F=Q2x4πε0(h2+x2)
and sinθ=R√(h2+x2)
Hence Q2xR4πε0(h2+x2)3/2=[MR22+MR2]α
or α=Q2x6πε0MR(h2+x2)3/2
for x<<h,α≅−Q2x6πε0MRh3
α=aR≅−Q2x6πε0MRh3
Negative sign is being introduced because angular acceleration and angular displacement are opposite to each other. Thus, ltbr> a=Q2x6πε0MRh3
Hence, ω=√Q26πε0MRh3
T=2π√6πε0MRh3Q2=2π(hQ)√(6πε0Mh).
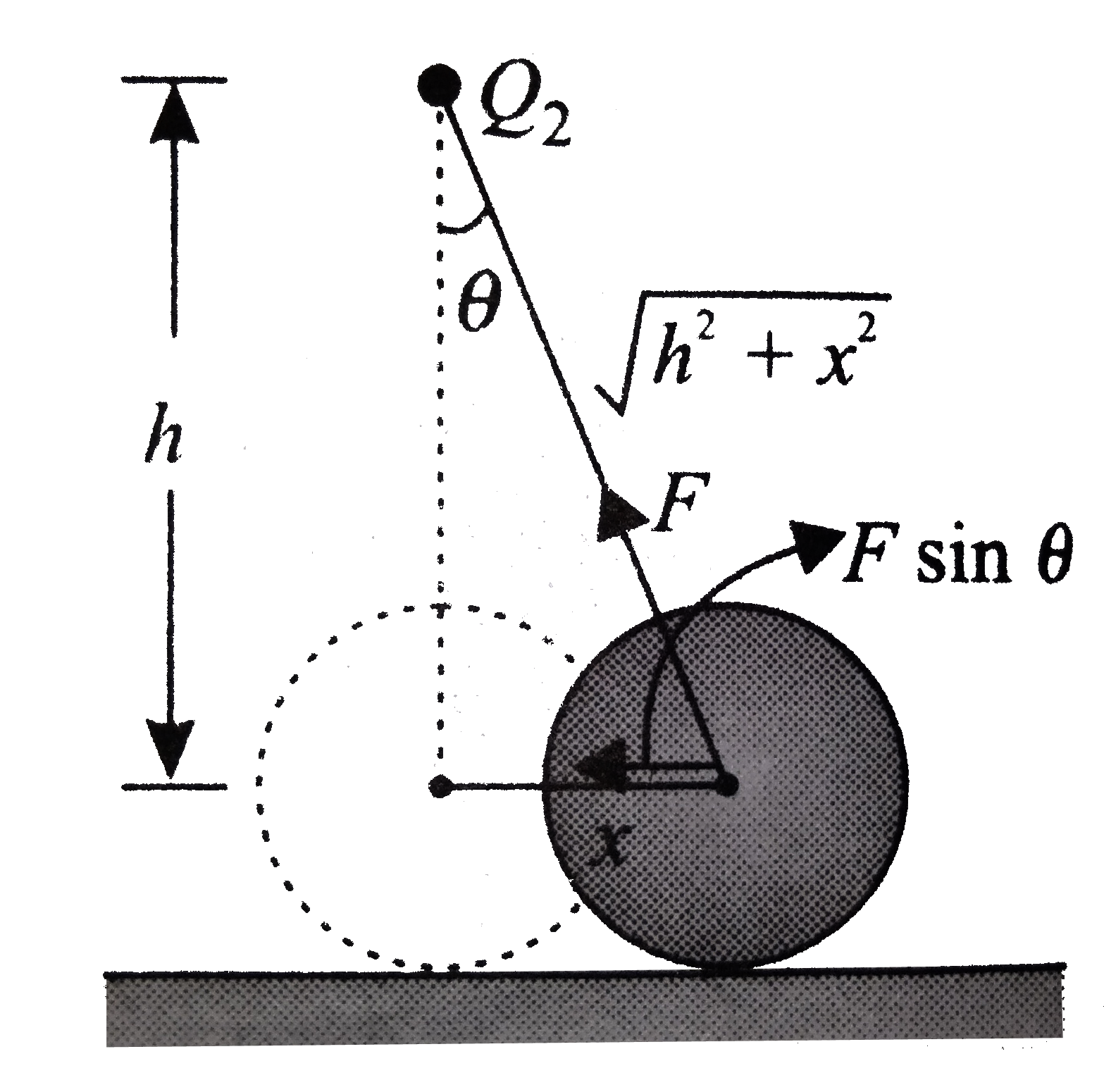
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Charge Q is uniformly distributed on the rim of a thin insulating disc of mass m which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field B, perpendicular to the plane of the disc is switched on ?

View SolutionA uniform solid disc of mass 1 kg and radius 1m is kept on a rough horizontal surface.

Two forces of magnitude 2N and 4N have been applied on the disc as shown in the figure. Linear acceleration of the center of mass of the disc is if there is no slipping is
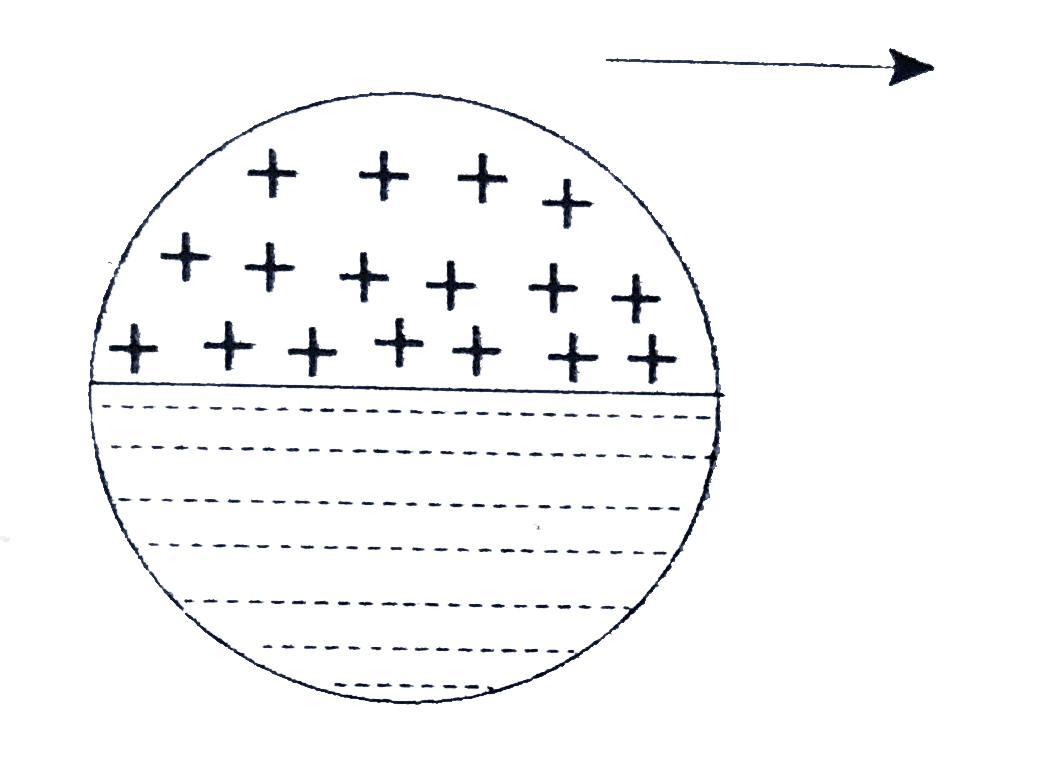
View SolutionA disc having uniform surface charge density in upper part +ρ and −ρ in lower half placed on rough horizontal surface as shown in figure. A uniform electric field is set up as shown if mass of disc is M and its radius is R as well sufficient friction is present to prevent slipping. The acceleration of disc is
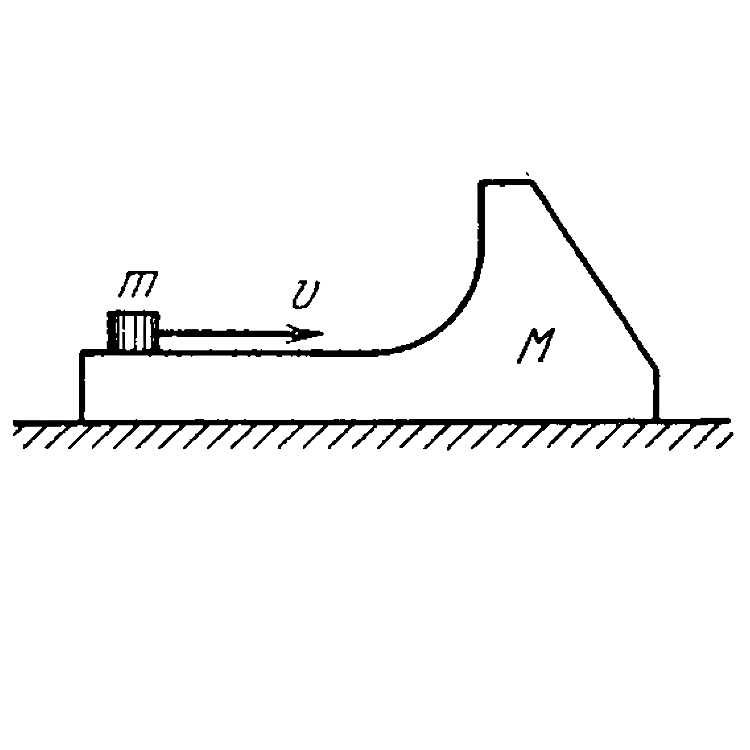
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
View SolutionFour point charges qA=2μC,qB=−5μC,qC=2μCandqD=−5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the square ?
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

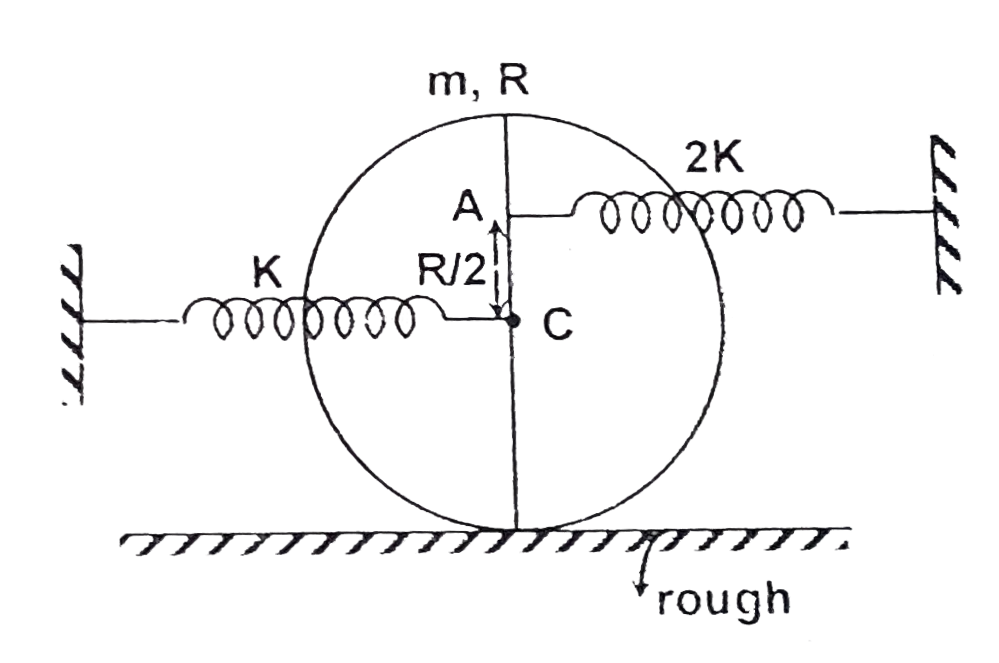
View SolutionA uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
View Solution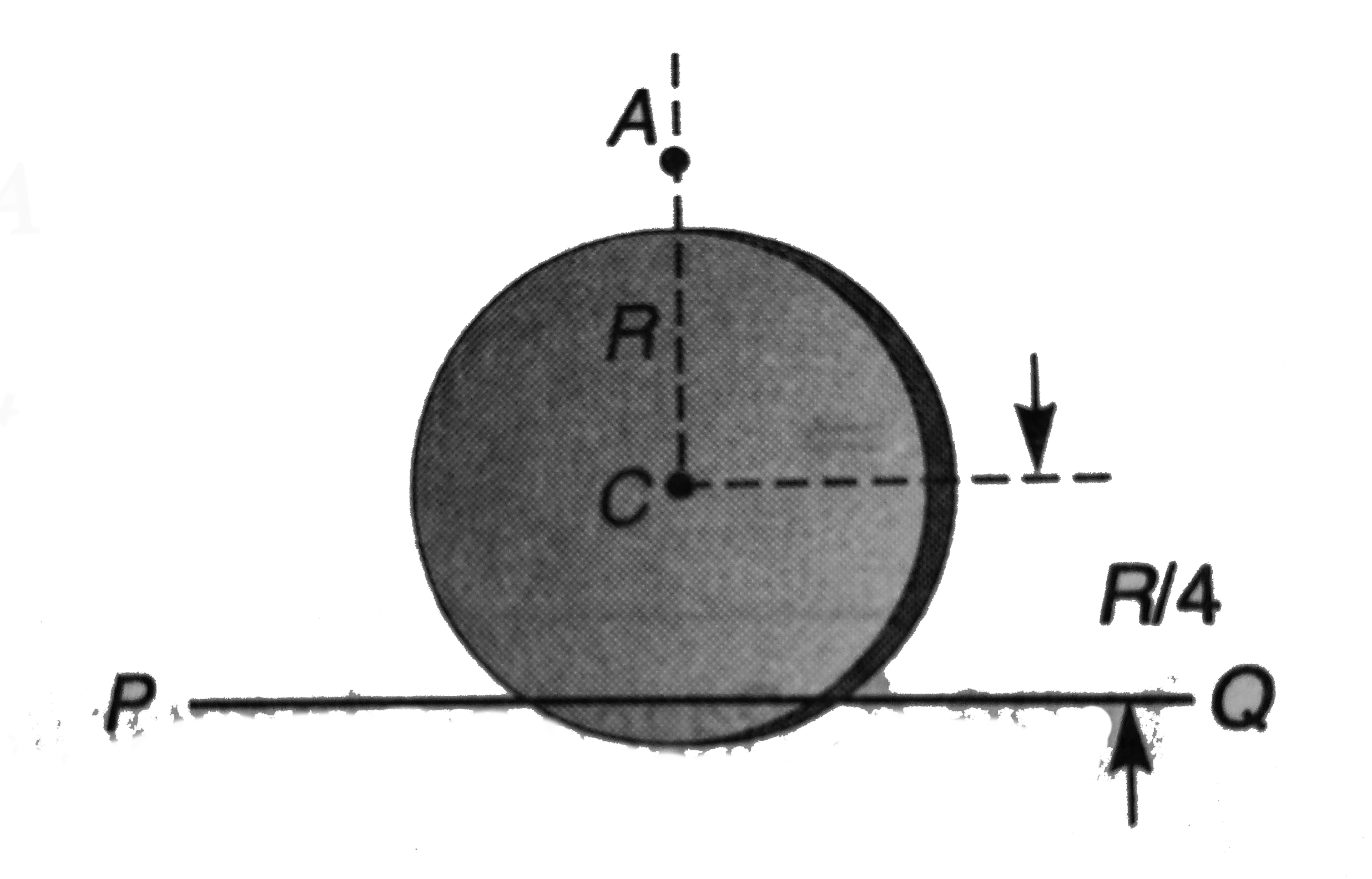
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionA spherical conductor A contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge q1 at the center of one cavity and q2 at the center of the other cavity . Another charge q3 is placed at a large distance r from the center of the spherical conductor.

If q1 is displaced from its center slightly (being always inside the same cavity ), then the correct representation of field lines inside the same cavity is
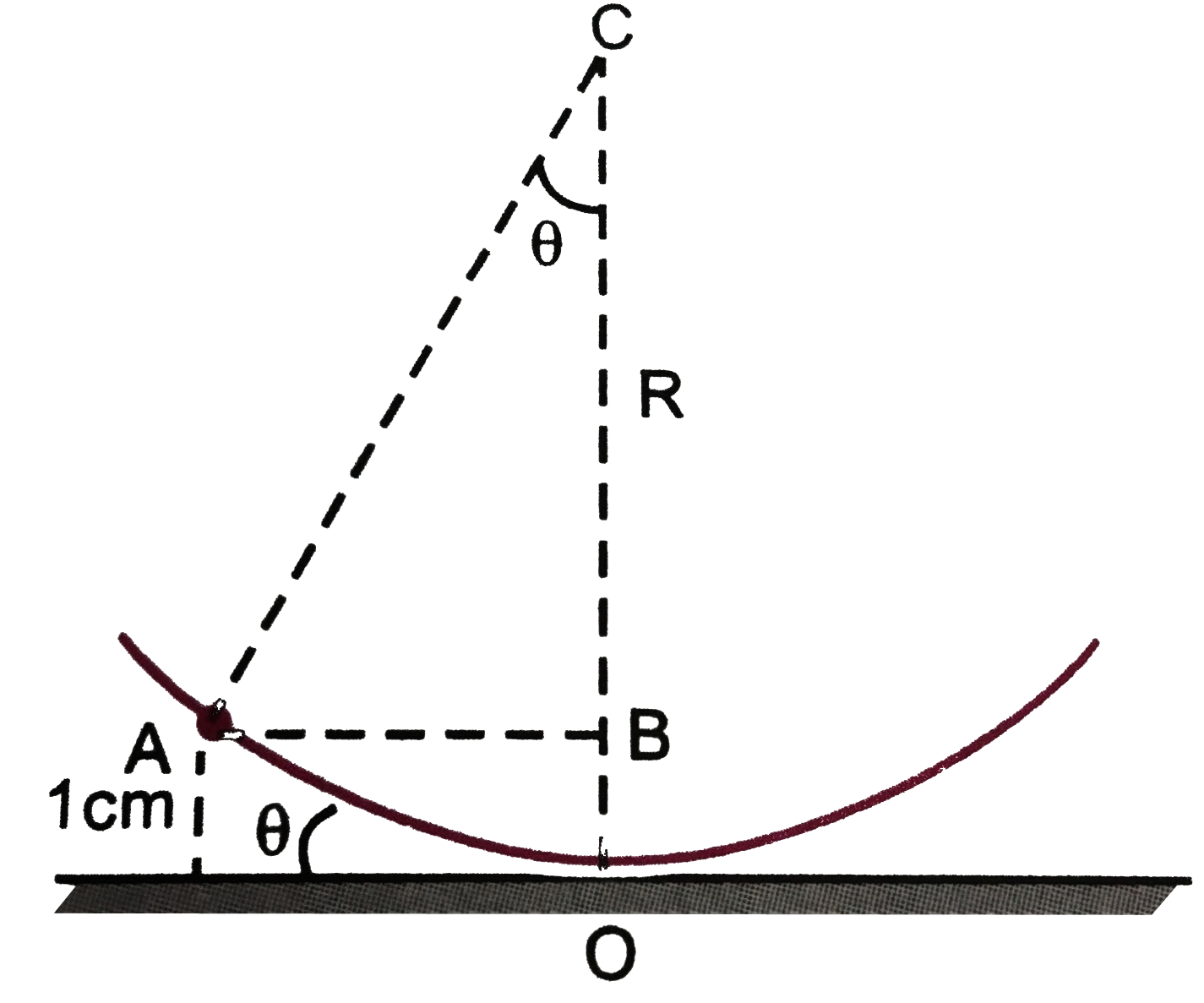
View SolutionA particle of mass 1 g executes an oscillatory motion on the concave surface of a spherical dish of radius 2m placed on a horizontal plane, Figure . If the motion of the particle begins from a point on the disc at a height of 1 cm. from the horizontal plane and coefficient of friction is 0.01 , find the total distance covered by the particle before coming to rest.
View Solution
