A point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
QR28πε0x4
3QR28πε0x4
5QR28πε0x4
7QR28πε0x4
The correct Answer is:B
To find the magnitude of the electric field strength vector at a point lying on the axis of a thin ring with a point charge at its center, we can follow these steps:
Step 1: Understand the Configuration
We have a point charge q located at the center of a thin ring of radius R that has a uniformly distributed charge of −q. We need to find the electric field at a point P on the axis of the ring at a distance x from its center, where x≫R.
Step 2: Determine the Electric Field Due to the Point Charge
The electric field E1 due to the point charge q at point P can be calculated using Coulomb's law:
E1=kqx2
where k is Coulomb's constant.
Step 3: Determine the Electric Field Due to the Ring Charge
The electric field E2 due to the uniformly charged ring can be derived from the principle of superposition. The electric field at point P due to the ring is directed along the axis of the ring and can be expressed as:
E2=−k(−q)x(x2+R2)3/2
Here, the negative sign indicates that the electric field due to the negative charge is directed towards the ring.
Step 4: Combine the Electric Fields
The net electric field E at point P is the vector sum of E1 and E2:
E=E1+E2=kqx2−k(−q)x(x2+R2)3/2
Step 5: Simplify the Expression
Since x≫R, we can approximate x2+R2≈x2. Thus, we can simplify E2:
E2≈−k(−q)x(x2)3/2=−k(−q)xx3=kqx2
Now substituting this back into the expression for the net electric field:
E≈kqx2+kqx2=2kqx2
Step 6: Final Expression
Thus, the magnitude of the electric field strength vector at point P is:
E≈2kqx2
Step 7: Substitute Coulomb's Constant
If we substitute k=14πϵ0:
E≈2⋅14πϵ0⋅qx2=q2πϵ0x2
Final Answer
The magnitude of the electric field strength vector at point P is:
E=q2πϵ0x2
We have a point charge q located at the center of a thin ring of radius R that has a uniformly distributed charge of −q. We need to find the electric field at a point P on the axis of the ring at a distance x from its center, where x≫R.
The electric field E1 due to the point charge q at point P can be calculated using Coulomb's law:
E1=kqx2
where k is Coulomb's constant.
The electric field E2 due to the uniformly charged ring can be derived from the principle of superposition. The electric field at point P due to the ring is directed along the axis of the ring and can be expressed as:
E2=−k(−q)x(x2+R2)3/2
Here, the negative sign indicates that the electric field due to the negative charge is directed towards the ring.
The net electric field E at point P is the vector sum of E1 and E2:
E=E1+E2=kqx2−k(−q)x(x2+R2)3/2
Since x≫R, we can approximate x2+R2≈x2. Thus, we can simplify E2:
E2≈−k(−q)x(x2)3/2=−k(−q)xx3=kqx2
Now substituting this back into the expression for the net electric field:
E≈kqx2+kqx2=2kqx2
Thus, the magnitude of the electric field strength vector at point P is:
E≈2kqx2
If we substitute k=14πϵ0:
E≈2⋅14πϵ0⋅qx2=q2πϵ0x2
The magnitude of the electric field strength vector at point P is:
E=q2πϵ0x2
Topper's Solved these Questions
Similar Questions
A charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
 View Solution
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
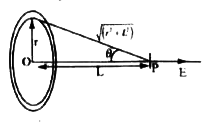 View Solution
View SolutionA point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (uniformly distributed a long its length).find the magnitudes of electric force between the two.
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
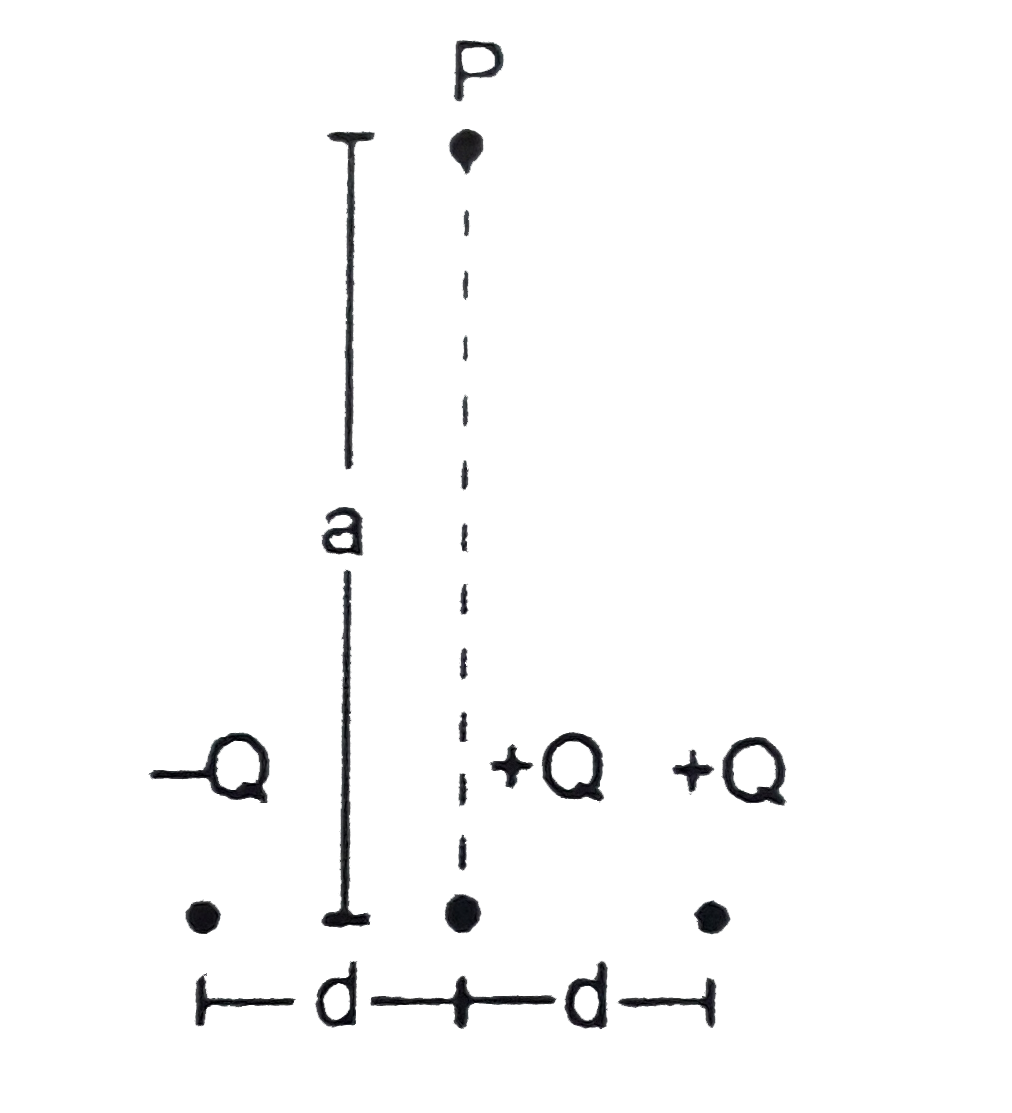 View Solution
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionA nonconducting ring of radius R has uniformly distributed positive charge Q. A small part of the ring.of length d, is removed (d<<R). The electric field at the centre of the ring will now be
View Solution

