A long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire. The wire has a charge per unit length of λ, and the cylinder has a net charge per unit length of 2λ. From this information, use Gauss's law to find (i) the charge per unit length on the inner and outer surfaces of the cylinder and (ii) the electric field outside the cylinder, a distance r from the axis.
i. Inside surface : Consider a cylinder surface within
the metal. Since E inside the conducting shell is zero,
the total charge inside the Gaussian surface must be
zero, so the char≥/≤n>h on the inner surface of the
cylinder is −λ.
Outer surface: The total charge on the mηl/<br>cyl∈deris<br>2lambdal = q_(in) + q_(out)orq_(out) = 2lambdal - q_(in),<br>whereq_(in) = -lambdal<br>q_(out) = 2 lambdal + lambdal = 3lambdal<br>Sotheoutscharge//lengthisq_(out)//l = 3 lambda.<br>ii.E≤ctricfieldoutsthecyl∈derE = (lambda_(net))/(2piepsilon_0r) = (3lambda)/(2piepsilon_0r)
radially outward.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
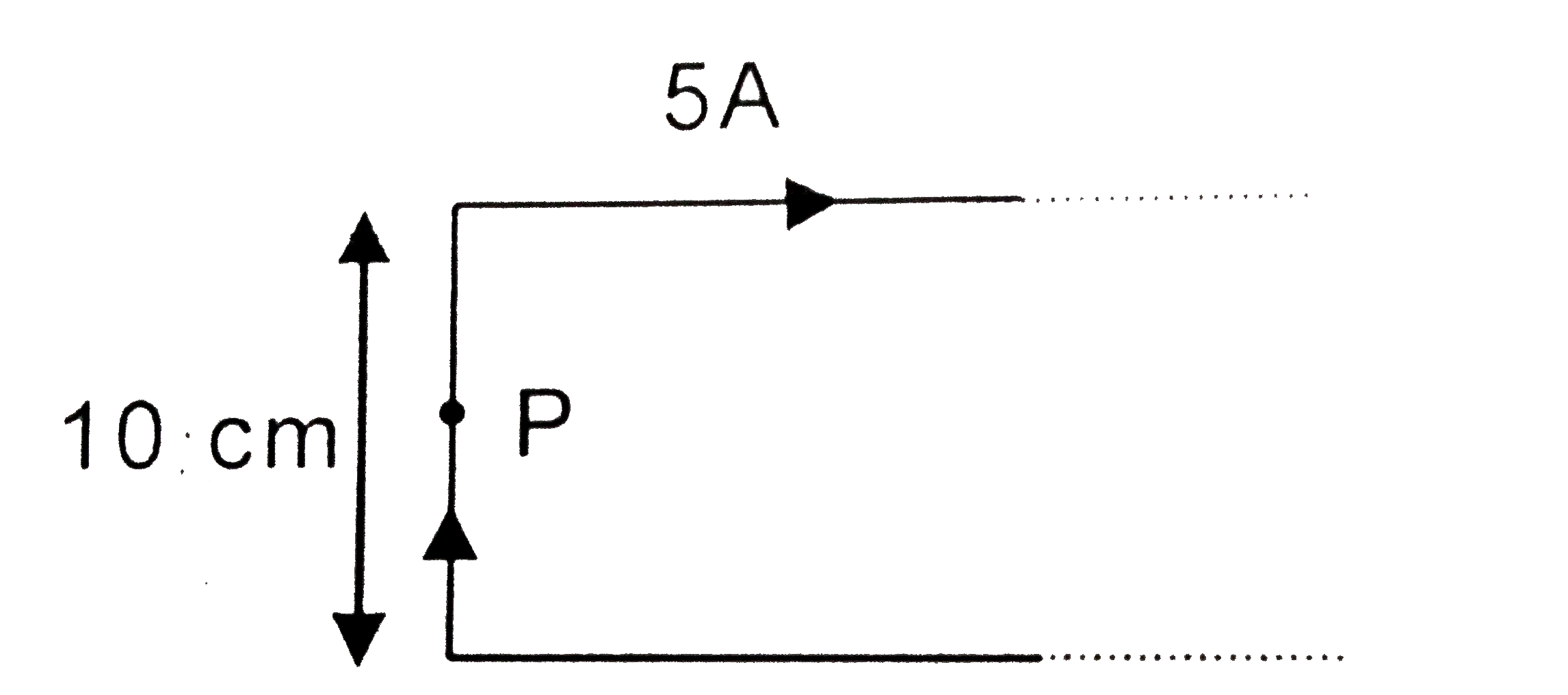
Find force per unit length at P
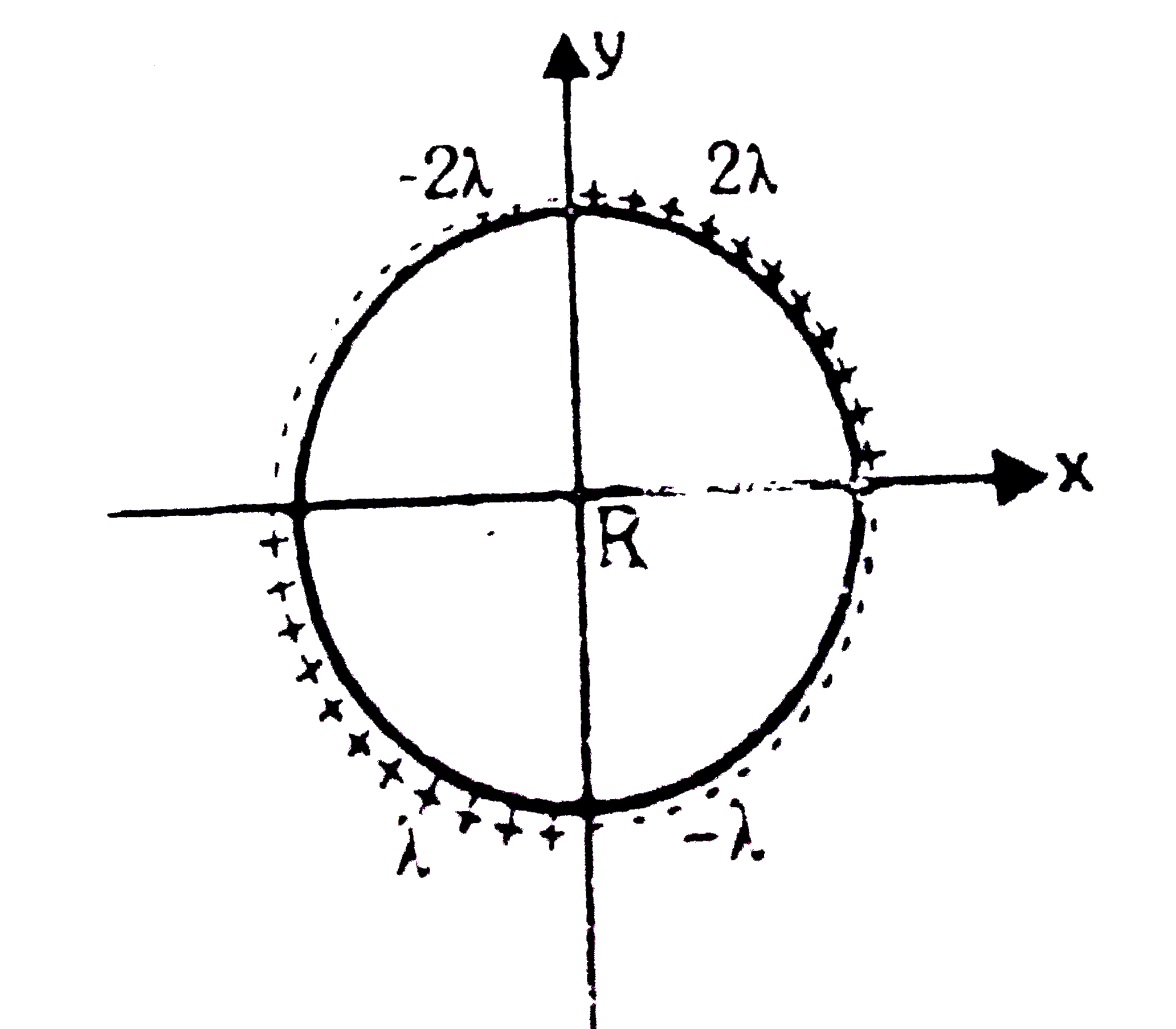
View SolutionThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.

View SolutionWhat is the charge per unit area in C/m2 of an infinite plane sheet of charge if the electric field produced by the sheet of charge has magnitude 3.0N/C?
View SolutionA long string with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View Solution
A small part of dl length is removed from a ring having charge per unit length λ. Find electric field at centre due to remaining ring.
View SolutionA thin bar of length L has a mass per unit length λ, that increases linerarly with distance from one end. If its total mass is M and its mass per unit length at the lighter end is λ0, then the distance of the centre of mass from the lighter end is
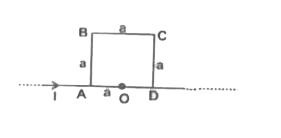
View SolutionThe resistance per unit length of the wires in segments AB, BC, CD, and AD are the same. The magnetic field due to the current at point O is
View Solution
