A sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

The electric field within the cavity or outside is the
superposition of the electric field due to the original
uncut sphere, plus the electric field due to a sphere of
the size of the cavity but with a uniform negative charge
density. The effective charge distribution is composed
of a uniformly charged sphere of radius R, charge
density ρ, superposed on it is a charge density - ρ filling
the cavity. An electric field →E1 is caused by the charge
distribution +ρ at a point →r inside the spherical cavity.
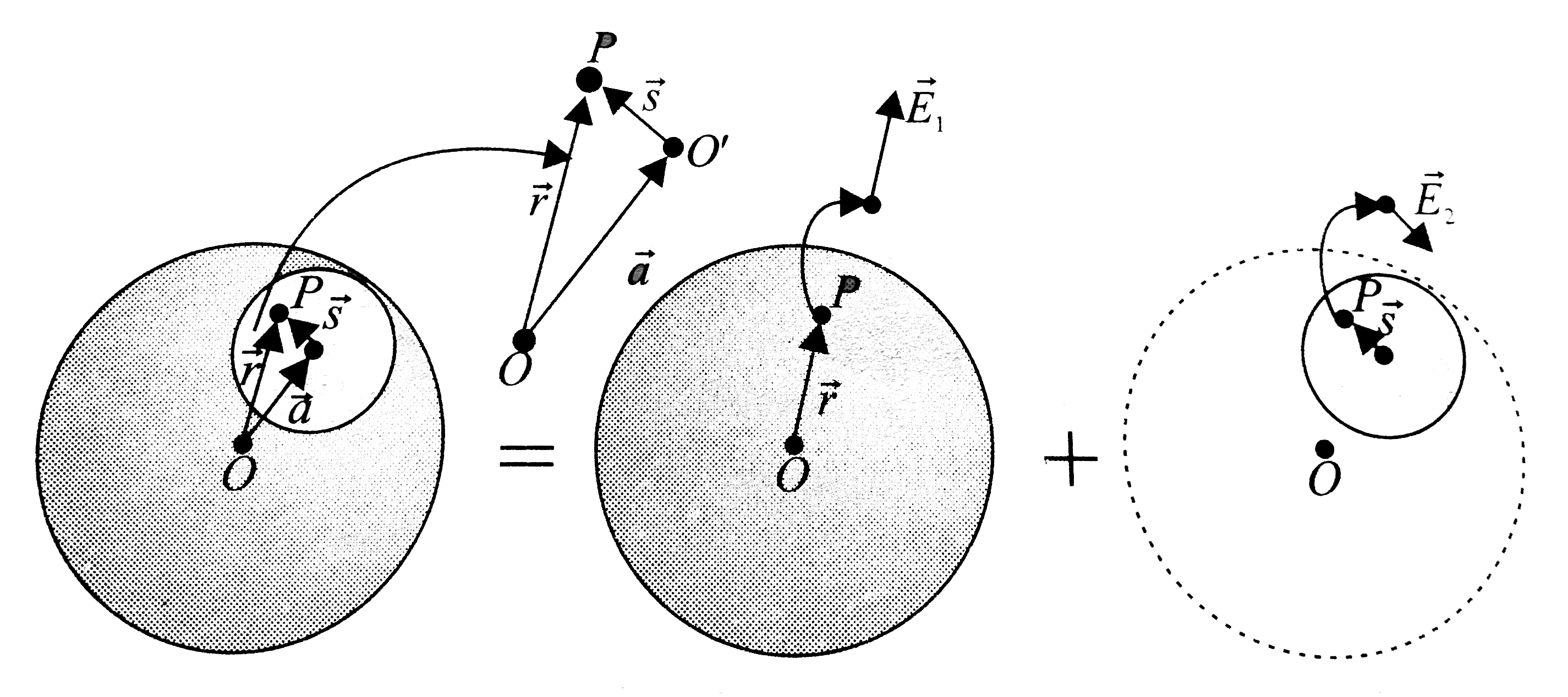
→E1=ρr3ε0r2=ρ→r3ε0
where ˆr is a unit vector in radial direction. Similarly, the electric field →E2 formed by the charge density −ρ
inside the cavity is
→E2=ρ(−→s)3ε0
Here, →s is the radius vector from the cavity centre to
the point P. From vector triangle
→r=→a+→sor→s=→r−→a
∴→E2=−ρ(→r−→a)3ε0
The resultant electric field inside the cavity is, therefore,
given by the superposition of →E1and→E2. So
→E=→E1+→E2=ρ→r3ε0+[−ρ(→r−→a)3ε0]=+ρ→a3ε0 = constant.
∴→E=ρ→a3ε0
ii. (a) Electric field at points inside the large sphere but
outside the cavity :
→E1=ρ→r3ε0
and →E2=14πε0q(−→s)s3=−(43πρb3)(→r−→a)4ε0|(→r−→a)|
The resultant electric field is
→E=→E1+→E2=ρ3ε0[→r−(b→r−→a)3(→r−→a)]
(b) Electric field at points outside the large sphere,
→E1=Qtotal)4πε0r3→r=43πR3ρ4πε0r3→r=R3ρ3ε0r3→r
→E2=Qtotal4πε0s3→s=−(43πb3ρ)4πε0(|→r−→a|)3(→r−→a)
=−ρb33ε0(|→r−→a|)3(→r−→a)
The resultant electric field is
→E=→E1+→E2=ρ3ε0[(Rr)3→r−(b→r−→a)3(→r−→a)]
∴E(→r)=⎧⎨⎩(ρ→a3ε0),⎛⎝ρ3ε0⎡⎣→r−(b|→r−→a|)3(→r−→a)⎤⎦⎞⎠,⎛⎝ρ3ε0⎡⎣(Rr)3→r−(b|→r−→a|)3(→r−→a)⎤⎦:}
Electric field inside the cavity
Electric field outside the cavity but inside the large cavity
electric field outside the large sphere .
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.2
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

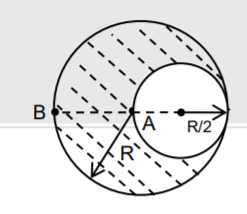
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionA solid spherical region, having a spherical cavity whose diameter R is equal to the radius of the spherical region, has a total charge Q. Find the electric field at a point P as shown in figure
 .
.
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

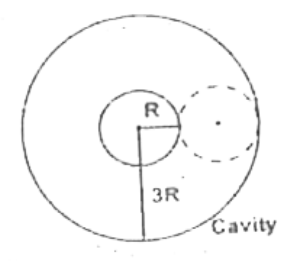
View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density σc/m3. It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View Solution
