A right circular imaginary cone is shown in figure A, B, and C are the points in the plane containing the base of the cone, while D is the point at the vertex of the cone. If ϕA,ϕB,ϕCandϕD represent the fulx through the curved surface of the cone when a point charge Q is at points A, B, C, and D. respectively. then.
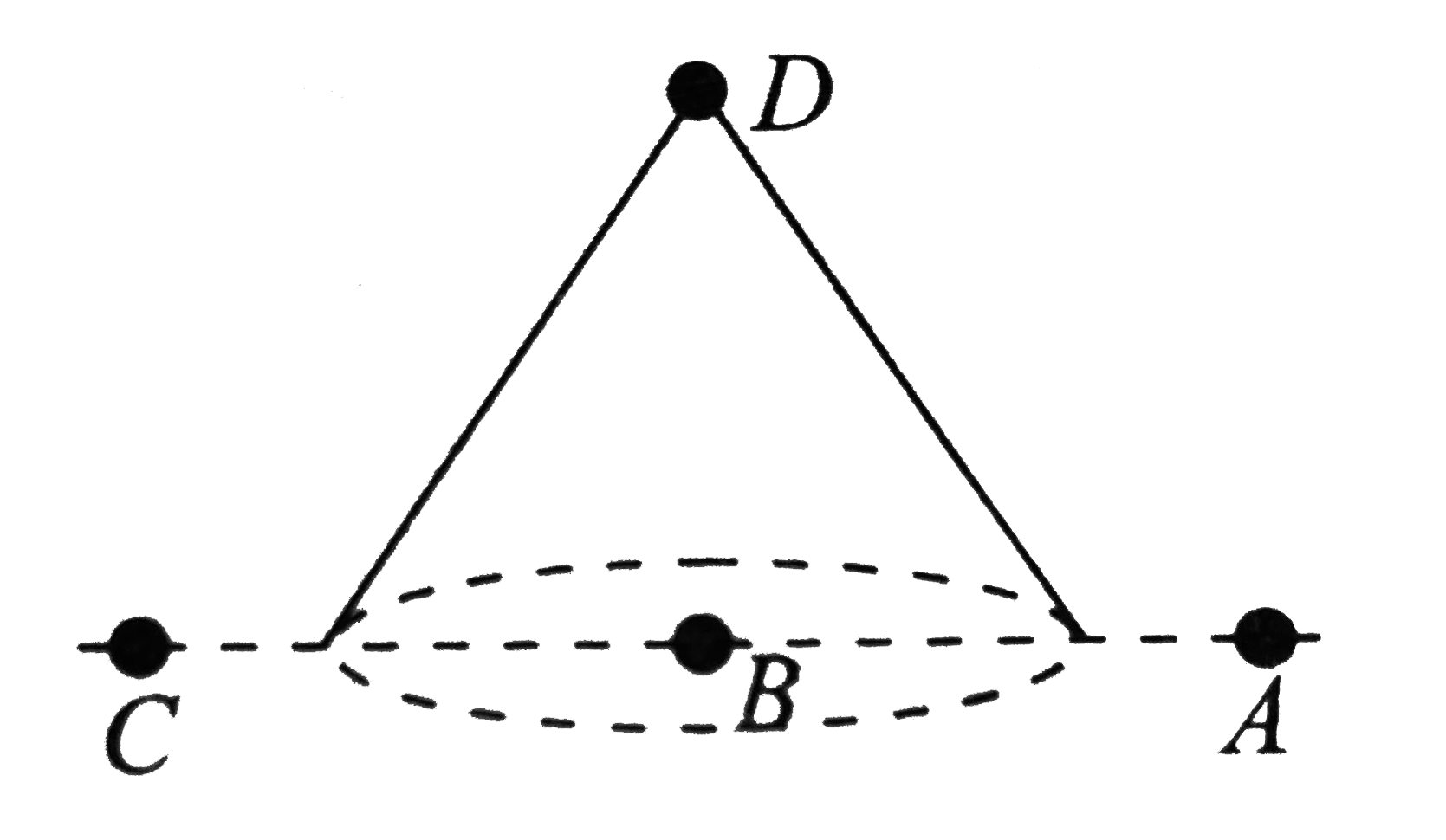
ϕA=ϕC≠0
ϕD≠0
ϕB=Q2ε0
ϕA=ϕC=ϕD=0
The correct Answer is:C, D
Flux through curved surface will be zero when charge is placed at A,C,orD. When charge is placed at B, flux through curved surface will be Q/2ε0.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct40videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
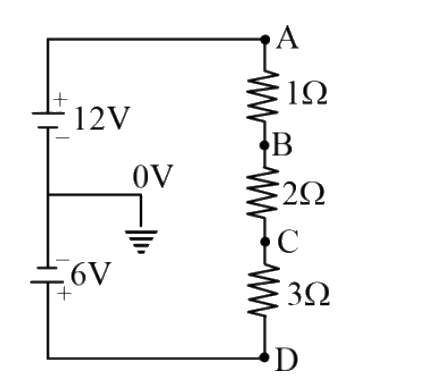
In the circuit diagram shown in Figure , the potentials of the points B, C and D are respectively -
 View Solution
View SolutionIn the electric field of a point chargde q, a cetrain charge is carried from point A to B,C,D and E. Then the work done
 View Solution
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View SolutionThe volume of a right circular cone is 9856 cm3 . If the diameter of the base is 28cm, find: (i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone.
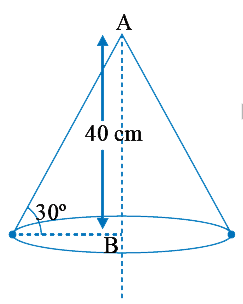
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
 View Solution
View SolutionThe number of surfaces of a cone has, is (a) 1 (b) 2 (c) 3 (d) 4
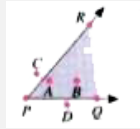
View SolutionWhich of these statements is not true ?
(a) Point A and B lie in the interior of the angle
(b) Points C and D lie in the exterior of the angle.
( c )Point P is the vertex of the angle .
(d) Point R is the vertex of the angle.
 View Solution
View SolutionIn Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
View SolutionA right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View Solution

