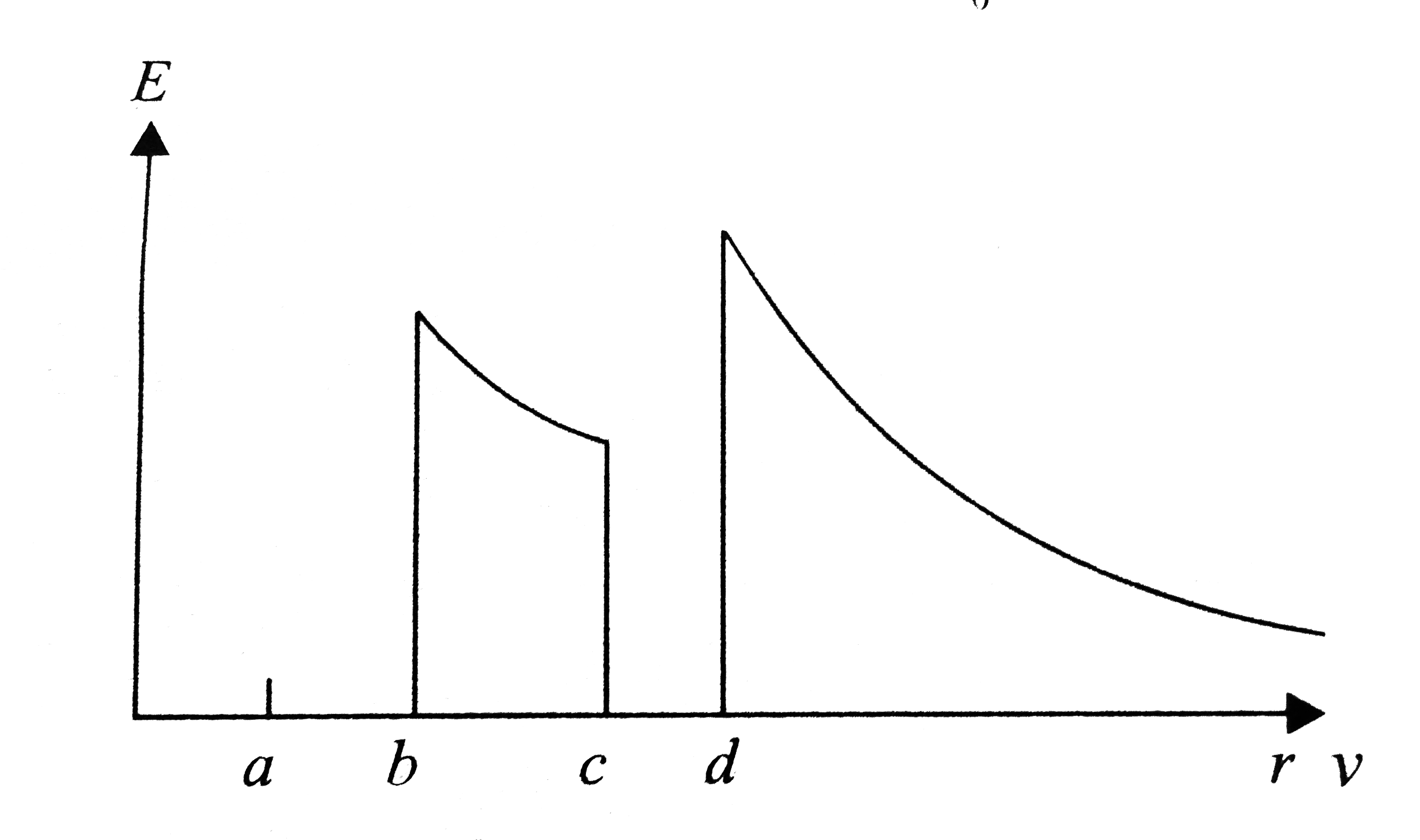
A small conducting spherical shell with inner radius a and outer radiu

A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for
ocr_image
$c < r < d$

View Solution

A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for
ocr_image
$a < r < b$

View Solution

A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for
ocr_image
$r < a$

View Solution

A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))
ocr_image
Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) $b < r < c$ (ii) $c < r < d$

View Solution

A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))
ocr_image
Find the electric in terms of q and the distance r from the common centre of the two shells for $r > d$ .

View Solution

A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting sphereical shell with inner radius c and outer radius d. The inner shell has total charge $+ 2 q$ and the outer shell has charge $+ 4 q$ .
a. Make a plot of the magnitude of the electric field versus r.
b. Calculate the electric field $(magnitude and direction in terms of q)$ and the distance r from the common centre of the two shell for $(i) r < a, (i i) a < r < b, (i i i)$ bltrltc, $(i v)$ cltrltd $, (v)$ rgtd $. S h o w u o u r r e s t - \in a g r a p h w i t h r a d i a l c o m p o \neq n t o f$ vecE $a s f u n c t i o n o f$ r.
c. What is the total charge on the
i. inner surface of the small shell,
ii. outer surface of the small shell,
iii. inner surface of the large shell,
iv. outer surface of the large shell?

View Solution

In Fig a conducting spherical shell of inner radius .x. and outer radius .y. is concentric with a larger conducting spherical shell of inner radius .a. and outer radius .b.. Inner shell has a total charge +3Q and the outer shell has a charge +5Q. Let r be the distance of any point from the common centre O.
ocr_image

View Solution

Consider the previous problem , let the outer shell have the charge $- 4 q$ . As in the above problem , the inner shell has the charge $+ 2 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for
$b < r < c$

View Solution

A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge $+ 2 q$ and the outer shell has charge $+ 4 q$ .
(i) What is the total charge on the (a) inner surface of the small shell, (b) outer surface of the small shell (c) inner surface of the large shell, (d) outer surface of the large shell ?
(ii) Calculate the electric field in terms of q and the the distance r from the common centre of two shells for (a) $r < a$ , (b) $a < r < b$ , (c) $b < r < c$ , (d) $c < r < d$ , (e) $r > d$
ocr_image

View Solution

Consider the previous problem , let the outer shell have the charge $- 4 q$ . As in the above problem , the inner shell has the charge $+ 2 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for
$c < r < d$

View Solution

The correct Answer is:B

i. $r < a . E = 0$ , since $Q = 0$ ( fig.S2.54)
ii. $a < r < b . E = 0$ , since $Q = 0$ .
iii. $b < r < c$ . Since $Q = + 2 q, E = \frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$
iv. C lt r lt d. E = 0 , since $Q = 0$ .
v. r gt d. E = (1)/( 4 pi epsilon_(0)) ( 6 q)/( r^(2)) $, \sin c e$ Q = + 6 q.

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-ELECTRIC FLUX AND GAUSS LAW-Comprehension

The correct Answer is:B

i. r < a . E = 0 , since Q = 0 ( fig.S2.54) ii. a < r < b . E = 0 , since Q = 0 . iii. b < r < c . Since Q = + 2 q , E = 1 4 π ε 0 2 q r 2 iv. C lt r lt d. E = 0 , since Q = 0 . v. r gt d. E = (1)/( 4 pi epsilon_(0)) ( 6 q)/( r^(2)) , sin c e Q = + 6 q.

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-ELECTRIC FLUX AND GAUSS LAW-Comprehension

i. $r < a . E = 0$ , since $Q = 0$ ( fig.S2.54)
ii. $a < r < b . E = 0$ , since $Q = 0$ .
iii. $b < r < c$ . Since $Q = + 2 q, E = \frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$
iv. C lt r lt d. E = 0 , since $Q = 0$ .
v. r gt d. E = (1)/( 4 pi epsilon_(0)) ( 6 q)/( r^(2)) $, \sin c e$ Q = + 6 q.