Consider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
The graph of the radial component of E as function of r will be
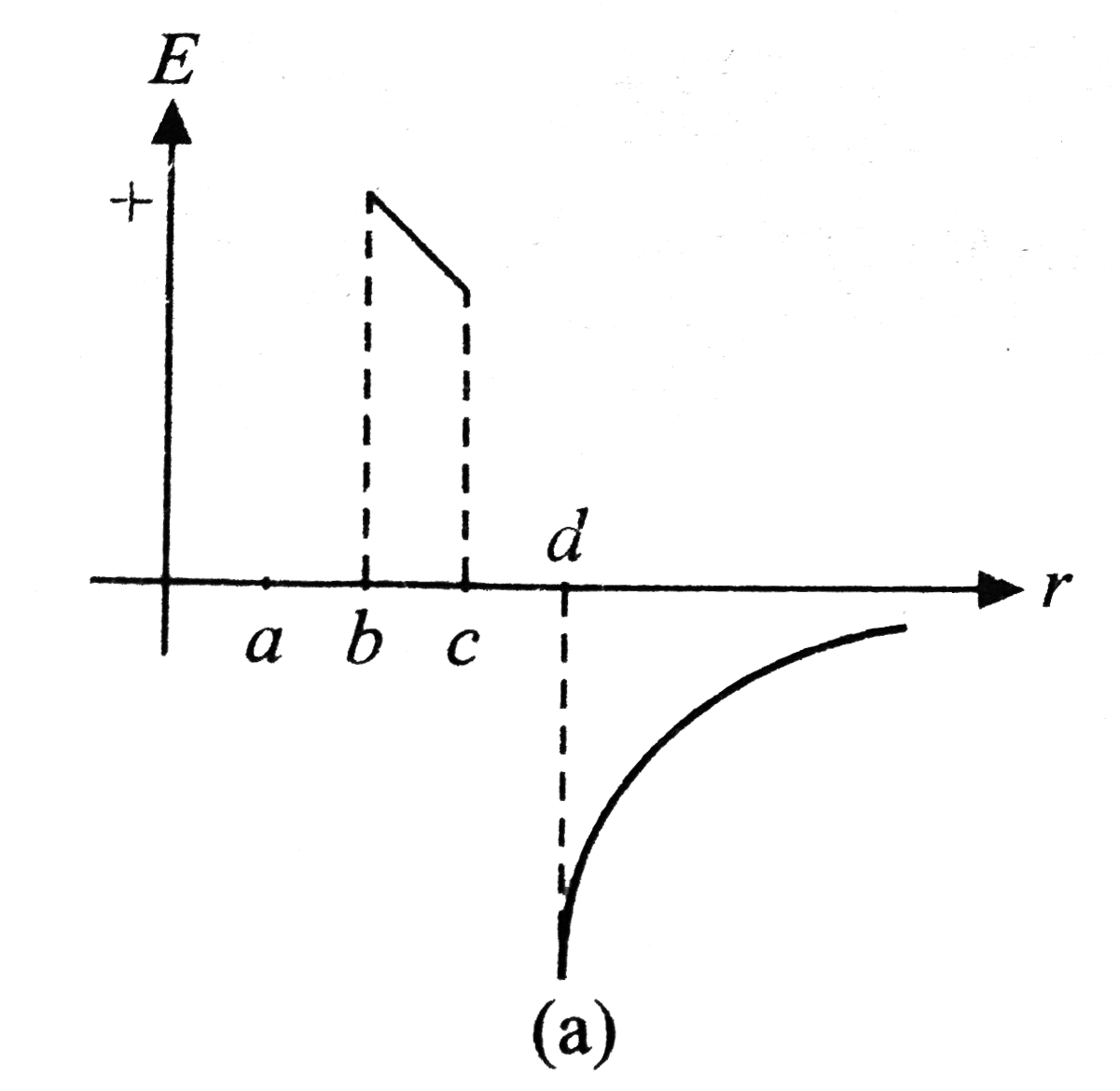

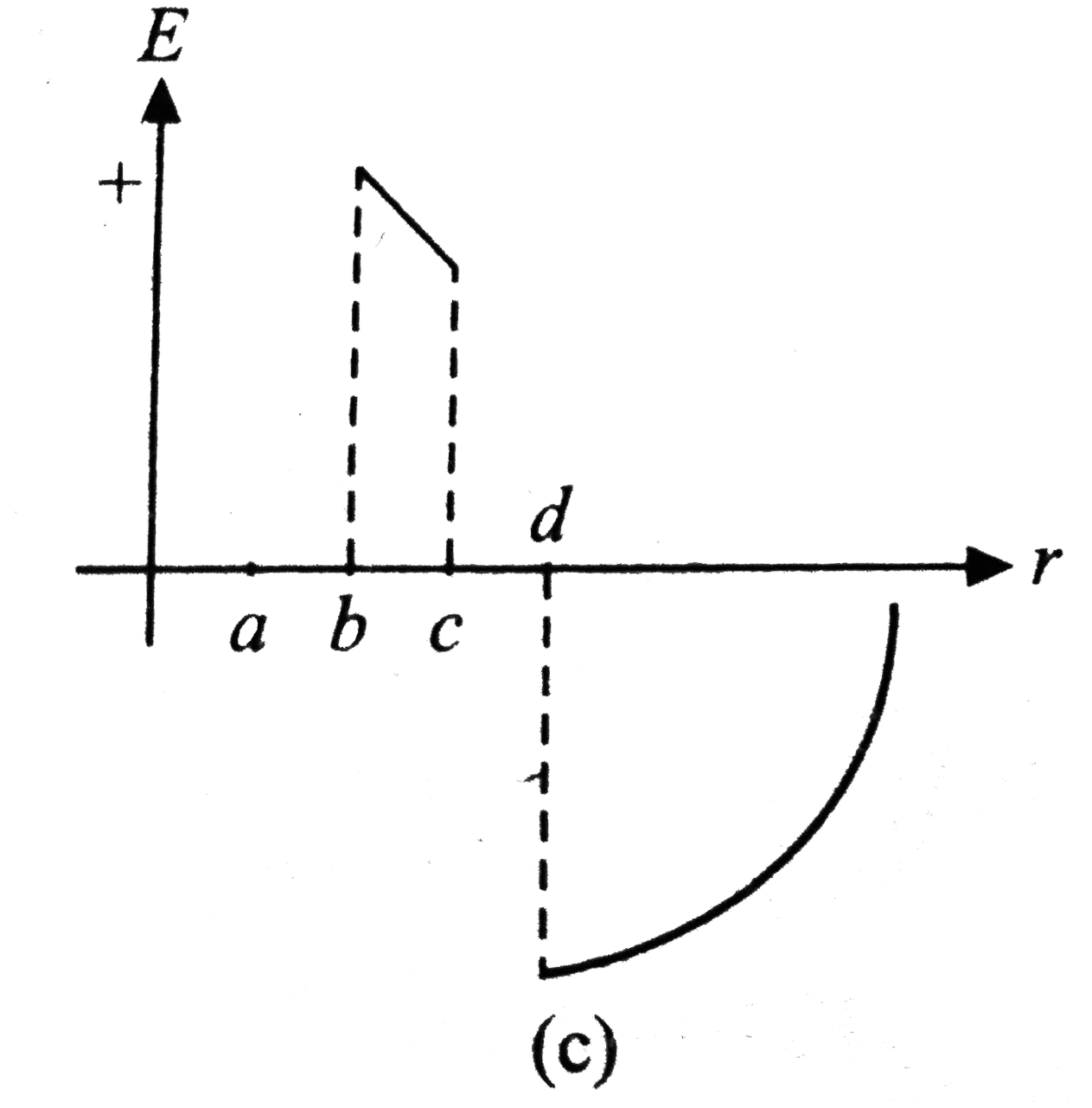

The correct Answer is:B
To solve the problem, we need to calculate the electric field E at different regions defined by the distances r from the common center of the two shells. We have two spherical shells: an inner shell with charge +2q and an outer shell with charge −4q.
1. Identify the Regions:
We will analyze the electric field in three distinct regions:
- Region I: Inside the inner shell ( r<R1 )
- Region II: Between the inner and outer shells ( R1<r<R2 )
- Region III: Outside the outer shell ( r>R2 )
2. Region I: Inside the Inner Shell ( r<R1 ):
- By Gauss's law, the electric field inside a conductor or a shell with no enclosed charge is zero.
- Therefore, E=0 for r<R1.
3. Region II: Between the Shells ( R1<r<R2 ):
- Here, we only consider the charge of the inner shell, since the outer shell's charge does not affect the electric field in this region.
- The enclosed charge Qenc=+2q.
- Applying Gauss's law:
∮→E⋅d→A=Qencϵ0
The area A=4πr2, thus:
E⋅4πr2=2qϵ0
Hence,
E=2q4πϵ0r2=q2πϵ0r2
4. Region III: Outside the Outer Shell ( r>R2 ):
- In this region, we consider the total enclosed charge, which is the sum of the charges of both shells.
- The total enclosed charge Qenc=+2q−4q=−2q.
- Again applying Gauss's law:
E⋅4πr2=−2qϵ0
Therefore,
E=−2q4πϵ0r2=−q2πϵ0r2
Summary of Electric Field in Different Regions:
- For r<R1: E=0
- For R1<r<R2: E=q2πϵ0r2
- For r>R2: E=−q2πϵ0r2
We will analyze the electric field in three distinct regions:
- Region I: Inside the inner shell ( r<R1 )
- Region II: Between the inner and outer shells ( R1<r<R2 )
- Region III: Outside the outer shell ( r>R2 )
- By Gauss's law, the electric field inside a conductor or a shell with no enclosed charge is zero.
- Therefore, E=0 for r<R1.
- Here, we only consider the charge of the inner shell, since the outer shell's charge does not affect the electric field in this region.
- The enclosed charge Qenc=+2q.
- Applying Gauss's law:
∮→E⋅d→A=Qencϵ0
The area A=4πr2, thus:
E⋅4πr2=2qϵ0
Hence,
E=2q4πϵ0r2=q2πϵ0r2
- In this region, we consider the total enclosed charge, which is the sum of the charges of both shells.
- The total enclosed charge Qenc=+2q−4q=−2q.
- Again applying Gauss's law:
E⋅4πr2=−2qϵ0
Therefore,
E=−2q4πϵ0r2=−q2πϵ0r2
- For r<R1: E=0
- For R1<r<R2: E=q2πϵ0r2
- For r>R2: E=−q2πϵ0r2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
Consider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
r<aView SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
b<r<cView SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
a<r<bView SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
c<r<dView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

a<r<bView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<aView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

b<r<cView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

c<r<dView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) b<r<c (ii) c<r<dView SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting sphereical shell with inner radius c and outer radius d. The inner shell has total charge +2q and the outer shell has charge +4q.
a. Make a plot of the magnitude of the electric field versus r.
b. Calculate the electric field (magnitude and direction in terms of q) and the distance r from the common centre of the two shell for (i)r<a,(ii)a<r<b,(iii)bltrltc,(iv)cltrltd,(v)rgtd.Showuourrest–∈agraphwithradialcompo≠ntofvecEasfunctionofr.
c. What is the total charge on the
i. inner surface of the small shell,
ii. outer surface of the small shell,
iii. inner surface of the large shell,
iv. outer surface of the large shell?View Solution

