Determine the electric field strength vector if the potential of this field depends upon x - and y - coordinates as :
(i) V=a(x2−y2)
(ii) V=axy.
To determine the electric field strength vector from the given electric potential functions, we will use the relationship between electric field (E) and electric potential (V). The electric field is given by the negative gradient of the electric potential:
E=−∇V
Where ∇ (nabla) is the gradient operator. In two dimensions (x and y), the gradient can be expressed as:
∇V=^i∂V∂x+^j∂V∂y
Thus, the electric field vector becomes:
E=−^i∂V∂x−^j∂V∂y
Now, let's solve the problem step by step for both parts.
Part (i): V=a(x2−y2)
1. Calculate the partial derivative with respect to x:
∂V∂x=∂∂x(a(x2−y2))=a⋅2x=2ax
2. Calculate the partial derivative with respect to y:
∂V∂y=∂∂y(a(x2−y2))=a⋅(−2y)=−2ay
3. Substitute the partial derivatives into the electric field equation:
E=−^i(2ax)−^j(−2ay)=−2ax^i+2ay^j
4. Final expression for the electric field vector:
E=−2ax^i+2ay^j
Part (ii): V=axy
1. Calculate the partial derivative with respect to x:
∂V∂x=∂∂x(a(xy))=a⋅y
2. Calculate the partial derivative with respect to y:
∂V∂y=∂∂y(a(xy))=a⋅x
3. Substitute the partial derivatives into the electric field equation:
E=−^i(ay)−^j(ax)=−ay^i−ax^j
4. Final expression for the electric field vector:
E=−ay^i−ax^j
Summary of Results:
- For V=a(x2−y2):
E=−2ax^i+2ay^j
- For V=axy:
E=−ay^i−ax^j
∂V∂x=∂∂x(a(x2−y2))=a⋅2x=2ax
∂V∂y=∂∂y(a(x2−y2))=a⋅(−2y)=−2ay
E=−^i(2ax)−^j(−2ay)=−2ax^i+2ay^j
E=−2ax^i+2ay^j
∂V∂x=∂∂x(a(xy))=a⋅y
∂V∂y=∂∂y(a(xy))=a⋅x
E=−^i(ay)−^j(ax)=−ay^i−ax^j
E=−ay^i−ax^j
- For V=a(x2−y2):
E=−2ax^i+2ay^j
- For V=axy:
E=−ay^i−ax^j
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Determine the electric field strength vector if the potential of this field depends on X, coordinates as V = 10 axy
View SolutionDetermine the electric field strength vector if the potential of this field depends on x, coordinates as
(a) V=a(x2—y2) (b) V=axy
where, a is a constant.
View SolutionGravitational potential in x−y plan varies with x and y
coordinates as
V=x2y+2xy
Find gravitational field strength E.
View SolutionThe electric field strength depends only on the x, y, and z coordinates according to the law E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2, where a=280Nm2C−1 is a constant. If the potential difference between (3,2,6) and (0,3,4) is x2. What is the value of x.
View SolutionWhich of these is/are representing electrostatic field? (x and y are space coordinates)
View SolutionThe direction of the field B at P is
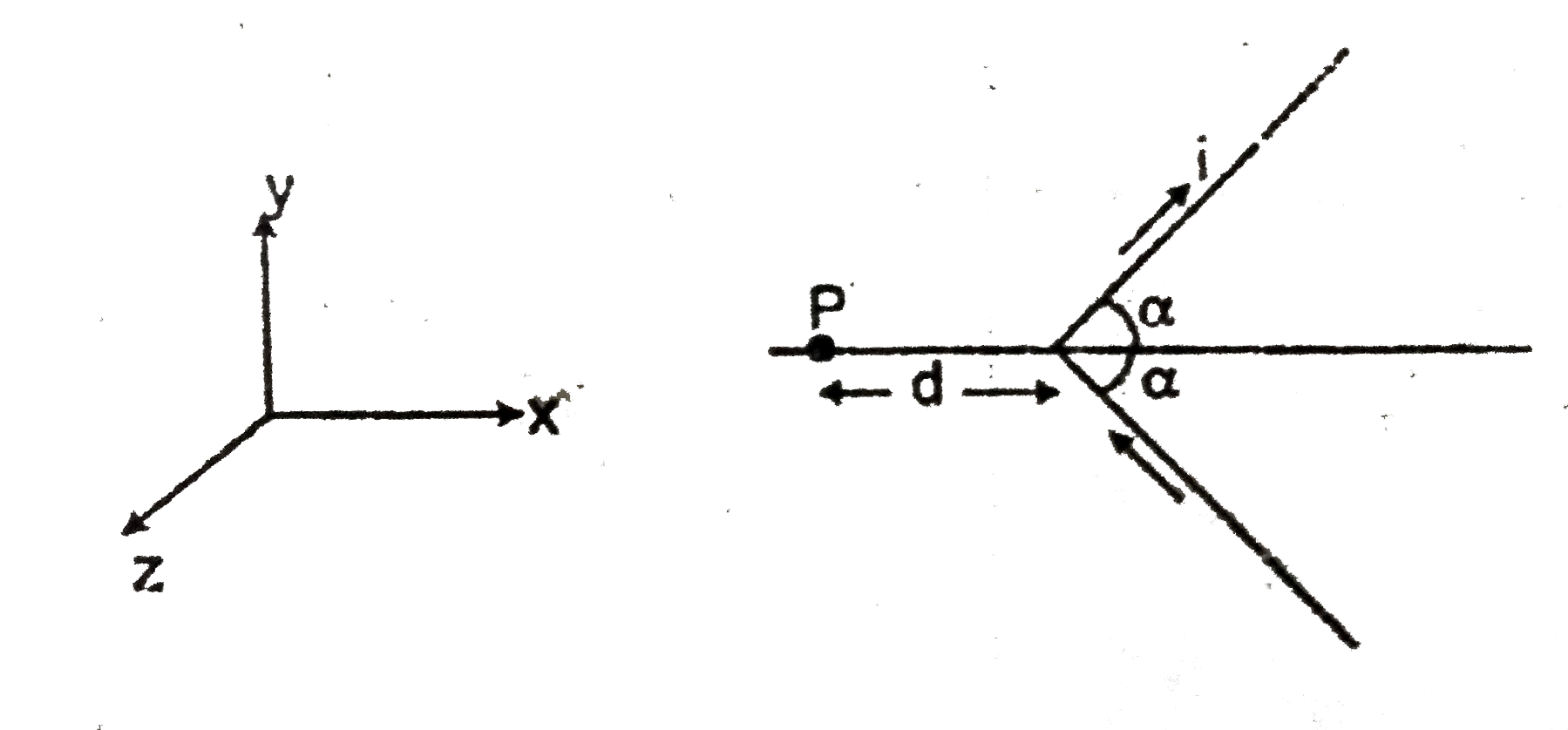
the V shaped wire is in x-y plane
View SolutionLet V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View SolutionDetermine graphically the coordinates of the vertices of a triangle, the equations of whose sides are: (i) y=x, y=2x and y+x=6 (ii) y=x, 3y=x and x+y=8
View SolutionThe electric field strenth vector is given by E=2.5xˆI+1.5yˆ.The potential at point (2,2,1) is (considering potential at origin to be zero)
View SolutionThe electrostatic potential V at any point (x, y, z) in space is given by V=4x2
View Solution
