Determine the electric field strength vector if the potential of this field depends on X, coordinates as V = 10 axy
-10 a (yˆi+xˆj)
−10[yˆi+xˆj]
−a[yˆi+xˆj]
−10a[xˆi+yˆk]
The correct Answer is:B
To determine the electric field strength vector from the given electric potential V=10Axy, we follow these steps:
Step 1: Understand the relationship between electric field and electric potential
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
where ∇V is the gradient of the potential.
Step 2: Calculate the components of the electric field
The electric field has two components in the Cartesian coordinates (x and y). We can express it as:
→E=Ex^i+Ey^j
Step 3: Find the x-component of the electric field
To find Ex, we need to compute:
Ex=−∂V∂x
Given V=10Axy, we differentiate with respect to x:
∂V∂x=10Ay
Thus,
Ex=−10Ay
Step 4: Find the y-component of the electric field
Next, we compute Ey:
Ey=−∂V∂y
Differentiating V=10Axy with respect to y:
∂V∂y=10Ax
So,
Ey=−10Ax
Step 5: Write the electric field vector
Now we can write the electric field vector:
→E=Ex^i+Ey^j=(−10Ay)^i+(−10Ax)^j
This can be simplified to:
→E=−10A(y^i+x^j)
Final Answer
Thus, the electric field strength vector is:
→E=−10A(y^i+x^j)
---
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
where ∇V is the gradient of the potential.
The electric field has two components in the Cartesian coordinates (x and y). We can express it as:
→E=Ex^i+Ey^j
To find Ex, we need to compute:
Ex=−∂V∂x
Given V=10Axy, we differentiate with respect to x:
∂V∂x=10Ay
Thus,
Ex=−10Ay
Next, we compute Ey:
Ey=−∂V∂y
Differentiating V=10Axy with respect to y:
∂V∂y=10Ax
So,
Ey=−10Ax
Now we can write the electric field vector:
→E=Ex^i+Ey^j=(−10Ay)^i+(−10Ax)^j
This can be simplified to:
→E=−10A(y^i+x^j)
Thus, the electric field strength vector is:
→E=−10A(y^i+x^j)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - C
53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Determine the electric field strength vector if the potential of this field depends on x, coordinates as
(a) V=a(x2—y2) (b) V=axy
where, a is a constant.
View SolutionDetermine the electric field strength vector if the potential of this field depends upon x - and y - coordinates as :
(i) V=a(x2−y2)
(ii) V=axy.
View SolutionThe electric field and the electric potential at a point are E and V respectively.
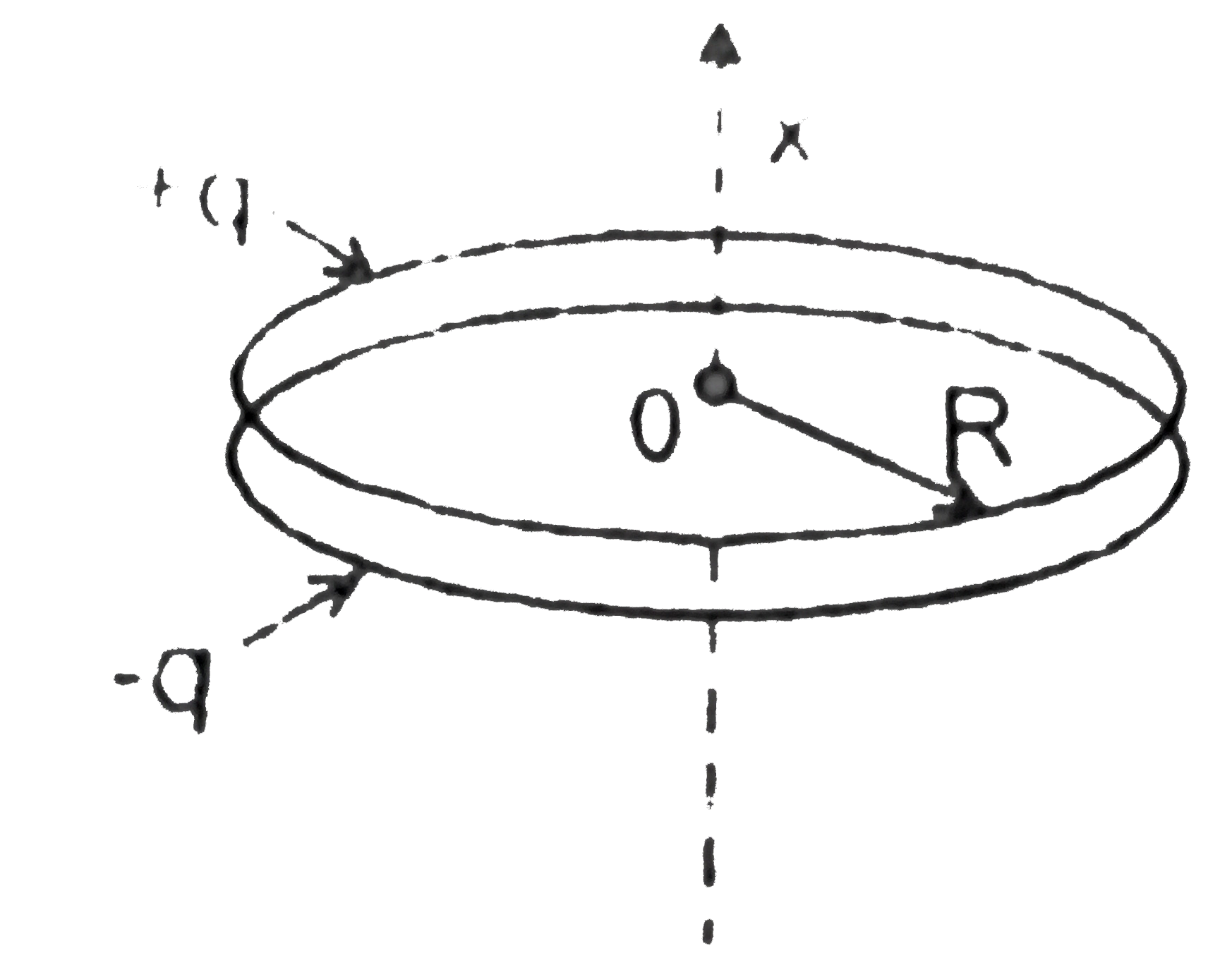
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
View SolutionA uniform electric field of 1 MV/m and a unifordi magnetic field of 10−2T were set up in some region of space. The electric field strength vector is perpendicular to the magnetic induction vector. A muon beam moves in a direction perpendicular to both vectors and passes without being deflected by the combined action of both fields. What is the velocity of the particles?
Can the charge of the particle and its sign be determined in this experiment?
View SolutionAssertion Due to two charges electric field and electric potential cannot be zero at some point simultaneously.
Reason Field is a vector quantity and electric potential is a scalar quantity
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionAssertion : Due to two point charges electric field and electric potential can't be zero at some point simultaneously.
Reason : Field is a vector quantity and potential a scalar quantity.
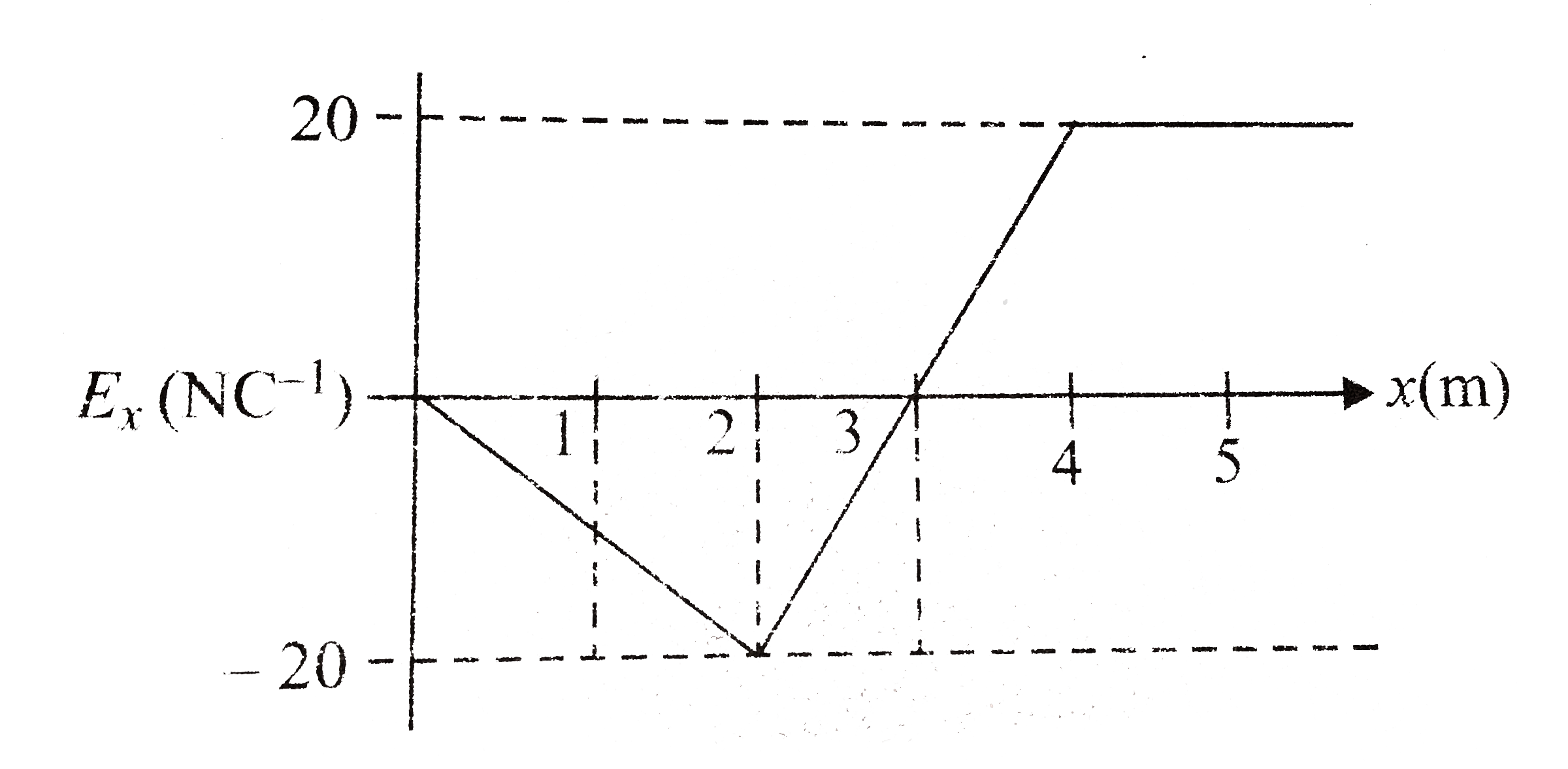
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
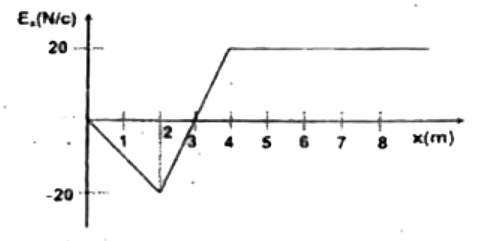
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
View Solution
