A very small sphere of mass having a charge q is held at a height of vertically above the center of a fixed conducting sphere of radius , carrying an equal charge q. When released, it falls until it is repelled back just before it comes in contact with the shpere as shown in Fig. 47. Calculate the charge .
To solve the problem, we will use the principle of conservation of energy, considering both gravitational potential energy and electric potential energy.
1. Identify Given Values:
- Mass of the small sphere, m=80g=0.08kg
- Height above the center of the conducting sphere, h=9m
- Radius of the conducting sphere, R=1m
- Acceleration due to gravity, g=10m/s2
2. Calculate the Gravitational Potential Energy (GPE):
- The gravitational potential energy when the small sphere is at height h:
GPE1=mgh=0.08×10×9=7.2J
3. Calculate the Electric Potential Energy (EPE):
- The electric potential energy between two charges q at a distance r is given by:
EPE=k⋅q2r
- Where k=14πϵ0≈9×109N m2/C2.
- At height h (9 m from the center of the conducting sphere), the distance r1=9m:
EPE1=k⋅q29
- At the surface of the conducting sphere (1 m from the center), the distance r2=1m:
EPE2=k⋅q21
4. Apply Conservation of Energy:
- The total energy at the height h equals the total energy just before the small sphere touches the conducting sphere:
GPE1+EPE1=GPE2+EPE2
- At the surface of the conducting sphere, the gravitational potential energy is zero (as we take it as the reference point):
7.2+k⋅q29=0+k⋅q21
5. Rearranging the Equation:
- Rearranging gives:
7.2=k⋅q21−k⋅q29
- Factor out k⋅q2:
7.2=k⋅q2(1−19)=k⋅q2⋅89
6. Solve for q2:
- Rearranging gives:
q2=7.2⋅98k
- Substitute k=9×109:
q2=7.2⋅98⋅9×109=7.28×109
- Simplifying gives:
q2=0.72109=0.72×10−9
7. Calculate q:
- Taking the square root:
q=√0.72×10−9=0.8485×10−5≈8.485×10−6C
- Converting to microcoulombs:
q≈8.485μC
Final Result
The charge q on the small sphere is approximately 8.485μC.
- Mass of the small sphere, m=80g=0.08kg
- Height above the center of the conducting sphere, h=9m
- Radius of the conducting sphere, R=1m
- Acceleration due to gravity, g=10m/s2
- The gravitational potential energy when the small sphere is at height h:
GPE1=mgh=0.08×10×9=7.2J
- The electric potential energy between two charges q at a distance r is given by:
EPE=k⋅q2r
- Where k=14πϵ0≈9×109N m2/C2.
- At height h (9 m from the center of the conducting sphere), the distance r1=9m:
EPE1=k⋅q29
- At the surface of the conducting sphere (1 m from the center), the distance r2=1m:
EPE2=k⋅q21
- The total energy at the height h equals the total energy just before the small sphere touches the conducting sphere:
GPE1+EPE1=GPE2+EPE2
- At the surface of the conducting sphere, the gravitational potential energy is zero (as we take it as the reference point):
7.2+k⋅q29=0+k⋅q21
- Rearranging gives:
7.2=k⋅q21−k⋅q29
- Factor out k⋅q2:
7.2=k⋅q2(1−19)=k⋅q2⋅89
- Rearranging gives:
q2=7.2⋅98k
- Substitute k=9×109:
q2=7.2⋅98⋅9×109=7.28×109
- Simplifying gives:
q2=0.72109=0.72×10−9
- Taking the square root:
q=√0.72×10−9=0.8485×10−5≈8.485×10−6C
- Converting to microcoulombs:
q≈8.485μC
The charge q on the small sphere is approximately 8.485μC.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
An isolated conduction sphere sphere whose radius R=1 m has a charge q=19nC. The energy density at the surfasce of the sphere is
View SolutionIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
View SolutionIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere the surface charge density of the plate -
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionWhen a small uncharged conducting ball of radius a=1cm and mass m=50g is dropped from a height h above the center of another large conducting sphere of radius b(=1m) having charge Q(=(100μC). It rises to a height h1(=2m) after the collision. Find the value of h. Assume that during the impact there is no dissipation of energy.
 .
.
View SolutionA small conducting sphere of radius a, carrying a charge +Q, is placed inside an equal and oppositely charged conducting shell of radius b such that their centers coincide. Determine the potential at a point which is at a distance c from center such that a<c<b.
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
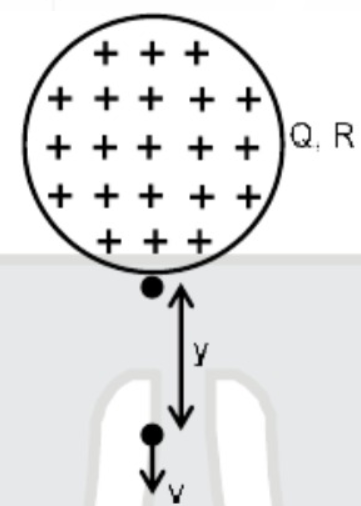
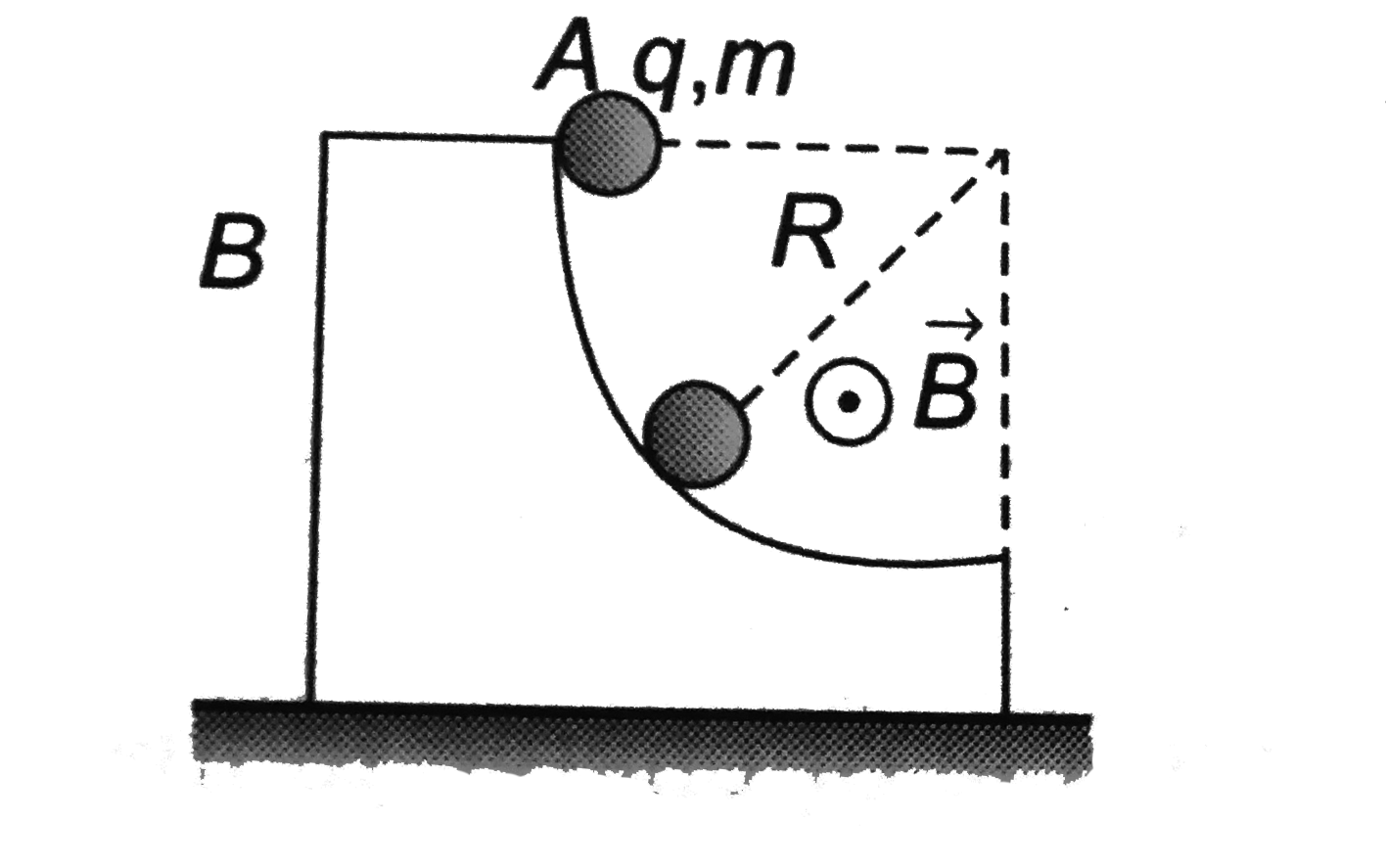
View SolutionIn the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View Solution
