A particle of mass 2 g and charge is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
The correct Answer is:D
To solve the problem, we will use the principle of conservation of energy. The initial potential energy of the charged particle will be converted into kinetic energy as it moves away from the fixed charge.
1. Identify the Given Values:
- Mass of the particle, m=2g=2×10−3kg
- Charge of the particle, q1=1μC=1×10−6C
- Fixed charge, q2=1mC=1×10−3C
- Initial distance from the fixed charge, r=1m
- Final distance from the fixed charge, d=10m
2. Write the Conservation of Energy Equation:
The total mechanical energy is conserved, so we have:
Initial Potential Energy+Initial Kinetic Energy=Final Potential Energy+Final Kinetic Energy
Since the particle is initially at rest, the initial kinetic energy is zero:
Ui+0=Uf+Kf
Where:
- Ui=k⋅q1⋅q2r
- Uf=k⋅q1⋅q2d
- Kf=12mv2
3. Substituting the Values:
Using k=9×109N m2/C2:
k⋅q1⋅q2r=k⋅q1⋅q2d+12mv2
Substituting the values:
9×109⋅(1×10−6)⋅(1×10−3)1=9×109⋅(1×10−6)⋅(1×10−3)10+12(2×10−3)v2
4. Calculating Potential Energies:
Ui=9×109⋅1×10−6⋅1×10−3=9×10−9J
Uf=9×10−910=9×10−10J
5. Substituting into the Energy Equation:
9×10−9=9×10−10+12(2×10−3)v2
Simplifying:
9×10−9−9×10−10=10−3v2
8.1×10−9=10−3v2
6. Solving for v2:
v2=8.1×10−910−3=8.1×10−6
7. Finding v:
v=√8.1×10−6=0.00284m/s≈2.84m/s
Final Answer:
The speed of the particle when it is at a distance of 10 m from the fixed charge is approximately 2.84 m/s.
- Mass of the particle, m=2g=2×10−3kg
- Charge of the particle, q1=1μC=1×10−6C
- Fixed charge, q2=1mC=1×10−3C
- Initial distance from the fixed charge, r=1m
- Final distance from the fixed charge, d=10m
The total mechanical energy is conserved, so we have:
Initial Potential Energy+Initial Kinetic Energy=Final Potential Energy+Final Kinetic Energy
Since the particle is initially at rest, the initial kinetic energy is zero:
Ui+0=Uf+Kf
Where:
- Ui=k⋅q1⋅q2r
- Uf=k⋅q1⋅q2d
- Kf=12mv2
Using k=9×109N m2/C2:
k⋅q1⋅q2r=k⋅q1⋅q2d+12mv2
Substituting the values:
9×109⋅(1×10−6)⋅(1×10−3)1=9×109⋅(1×10−6)⋅(1×10−3)10+12(2×10−3)v2
Ui=9×109⋅1×10−6⋅1×10−3=9×10−9J
Uf=9×10−910=9×10−10J
9×10−9=9×10−10+12(2×10−3)v2
Simplifying:
9×10−9−9×10−10=10−3v2
8.1×10−9=10−3v2
v2=8.1×10−910−3=8.1×10−6
v=√8.1×10−6=0.00284m/s≈2.84m/s
The speed of the particle when it is at a distance of 10 m from the fixed charge is approximately 2.84 m/s.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionFour particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
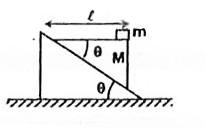
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View Solution
