shows two capacitors in series, the rigid central conducting section of length b being movable vertically.
 .
.
If the potentials of the upper and lower plates are V1 and V2 respectively, then potebtial of rigid segid secton is.
V1−(V1−V2)x(a−b)
V1−(V2−V1)x(a−b)
V1−(V1−V2)x(a+b)
V1−(V1−V2)x(a+b)
The correct Answer is:A
The circuit is equicalent to two capacitors in series.
 .
.
C1=ε0AA
C2=ε0A(a−b−x)
1Ceq=1ε0A[a−b−x+x]=(a−b)ε0A
We can reduce this structure in this srrucure in the following ciruit.
(V1−V)=(V1−V2)C2C1+C2
 .
.
V1−V=(V1−V2)ε0A(a−b−x)ε0Ax+ε0Aa−b−x
=(V1−V2)x(a−b)−(V1−V2)x(a−b).
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct
11 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Shows two capacitors in series, the rigid central conducting section of length b being movable vertically.
 .
.
The equivalent capacitance of the given structure is .
View SolutionFigure shows two capacitors in series. The rigid center section of length .b. is movable. The area of each plate is S. If the voltage difference between the plates is maintained constant at V0 The change in stored energy if the center section is removed is

View Solution
Knowledge Check
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
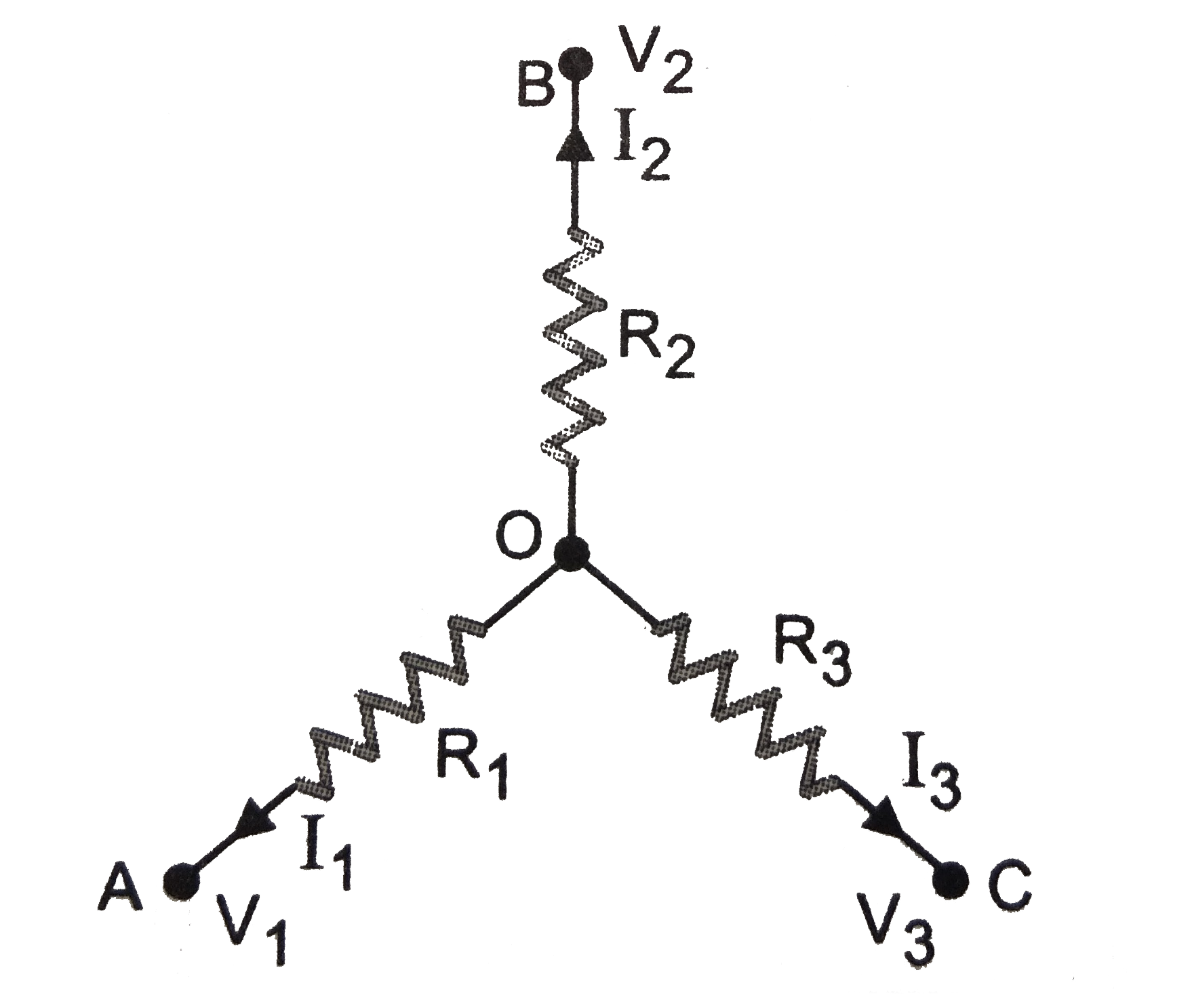 AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
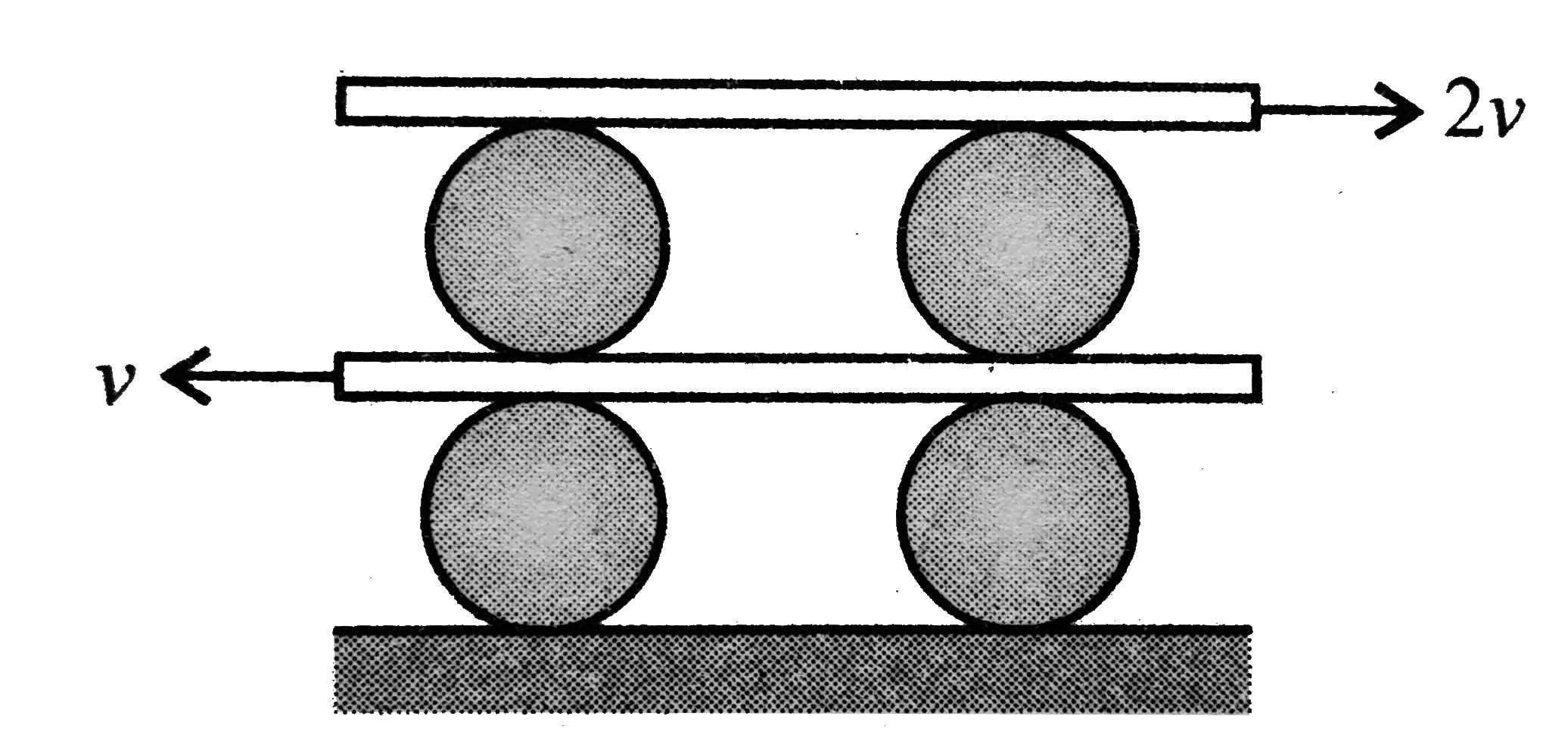 A1:3B3:1C1:2D2:1
A1:3B3:1C1:2D2:1
Three capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionTwo dielectric slabs of area of cross-section same as the area of the plates are introduced inside a capacitor as shown. Now, the capacitor is charged. If the potential of the upper plate of the capacitor is
VH and the potential of the lower plate is VL, the potential at the interface of the two slabs is:

View SolutionThree uncharged capacitors are connected as shown in the figure. If potentials at point P, Q and R are maintained at 1V, 2V, 3V respectively, then potential at O becomes
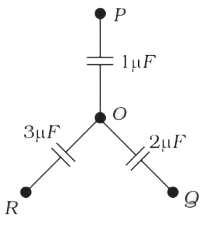 .
.
View SolutionTwo capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
View SolutionA system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is

View Solution
The pressures at A and B in the atmosphere are, respectively,
View Solution
