Calculate the current through each resistance in the given circuit. Also calculate the potential difference between the points a and b.
E1=6V,E2=8V,E3=10V,
R1=5Ω,R2=10Ω,R3=4Ω
Assume that all the cless have no internal resistance.
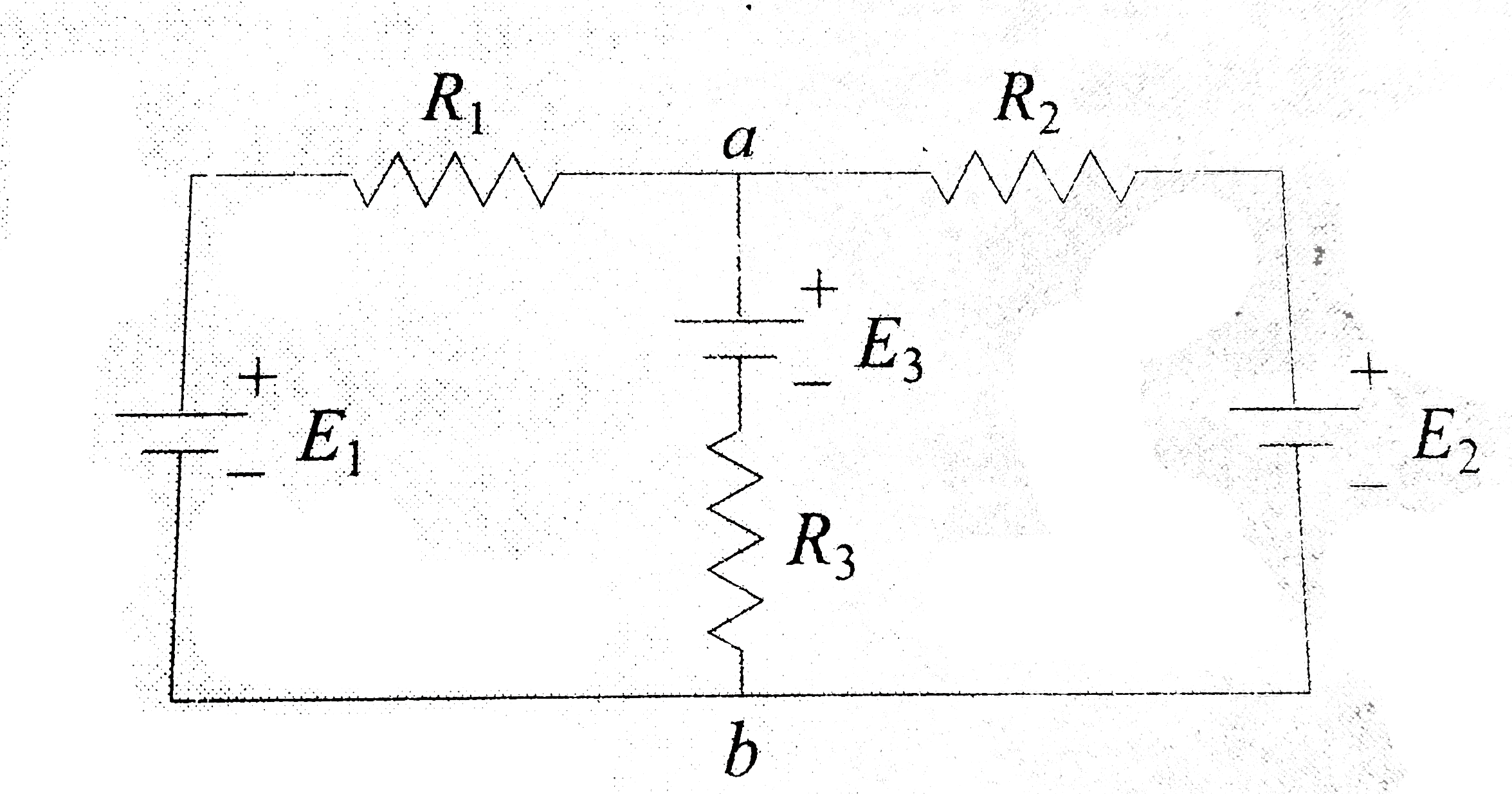
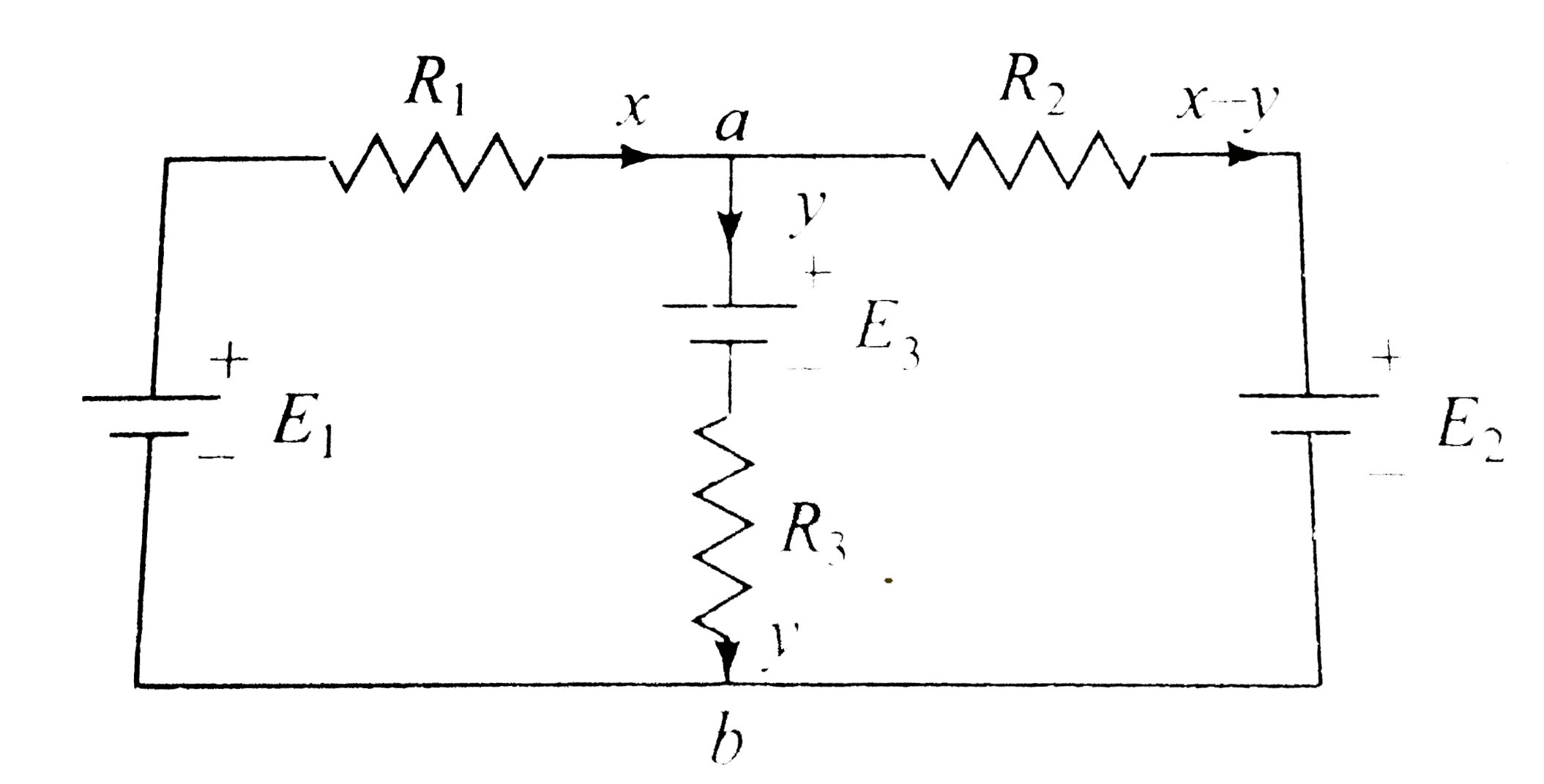
The process of solving a circuit involves three steps:
i. Assume unkonwns (x, y, ….) for currents in different
branches of the circuit. Use Kirchhoff's Current law at
the junctins so that the number of unknowns introduced
is minimum. Let x be the current through R1 and y be the
current through R3 as shown in Fig. 5.74. Kirchhoff's
current law at the junction a gives a current (x-y)
through R2

ii. Selectas many loops as the number of unknows introduced
for currents. Apply Kirchhoff's voltage law throgh every
loop. Going anticlockwise through the loop containing
R1andR3(starting from junction a), we get
+xR1−E1+yR3+E3=0
or 5x +4y = -4 ....(i)
Going clockwise through the loop containing R2andR3 (starting from juction a), we get
−R2(x−y)−E2+yR3+E3=0
or 5x - 7y =1 (ii)
Some currents may come out to be negative. This simply
means that their directions were incorrectly assumed. so the signs of the currents will given us the correct direction
of each current. Solving Eqs. (i) and (ii) we get
x=−2455andy=−511A
∴x−y=155A
This signs indicate that the direction of x and y were
assumed incorrectly, while the direction of (x-y) was
correct. So
current i1(through R1)=2455A toward left
current i2(through R2)=155 A toward right
current i3(through R3)=511 A upward
The current directions are shown in the circuit diagram
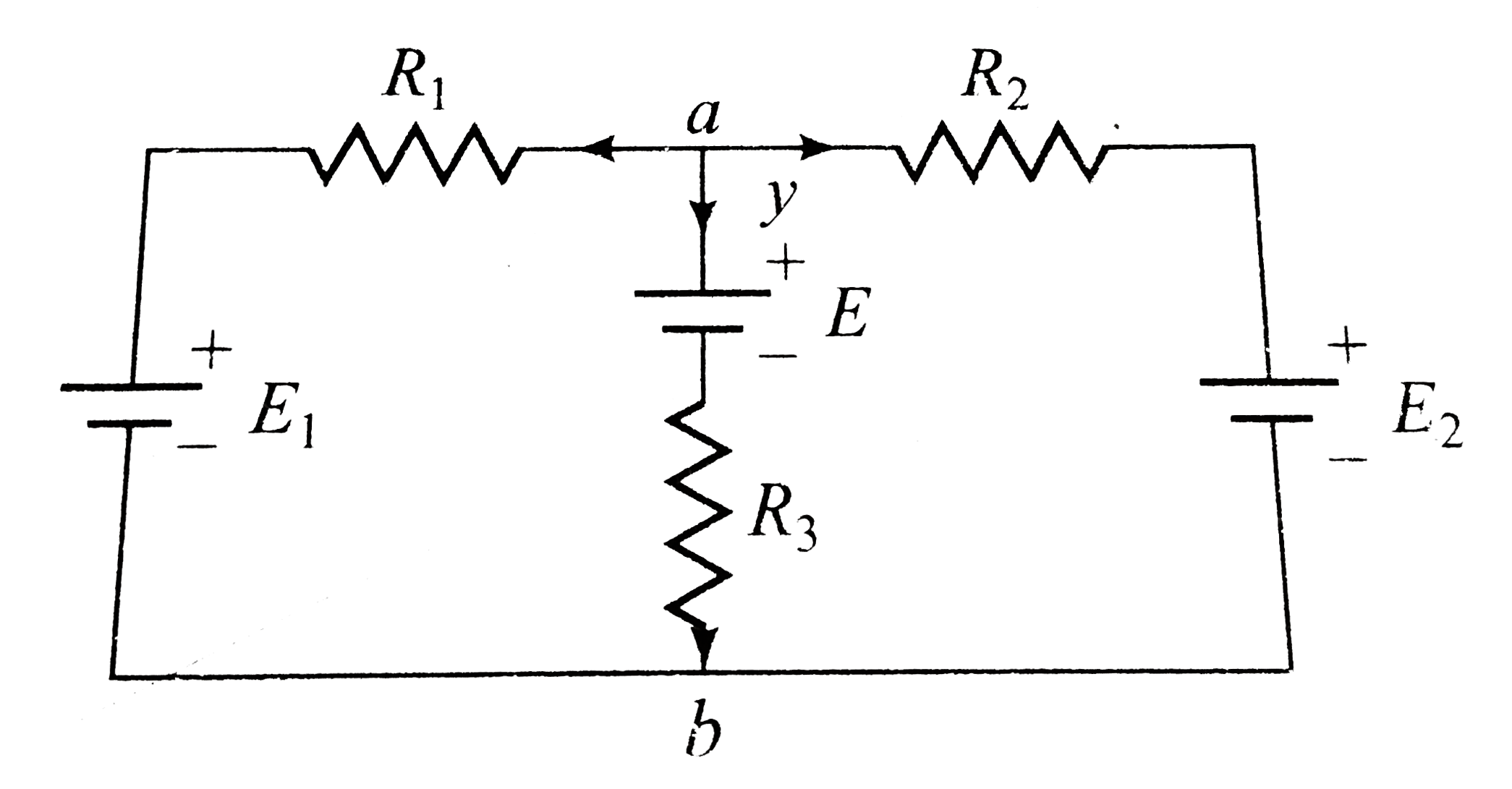
iii. Potential difference between a and b
The potentia difference between any two points in a
circuit is calculated by adding the changes in potential
while going through any path form one point to the other
point. Hence, let us go from b to a through R3.
Va−Vb=+yR3+E3=(−511)×4+10=9011v
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Calculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View SolutionCalculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionFind the current in each wire.
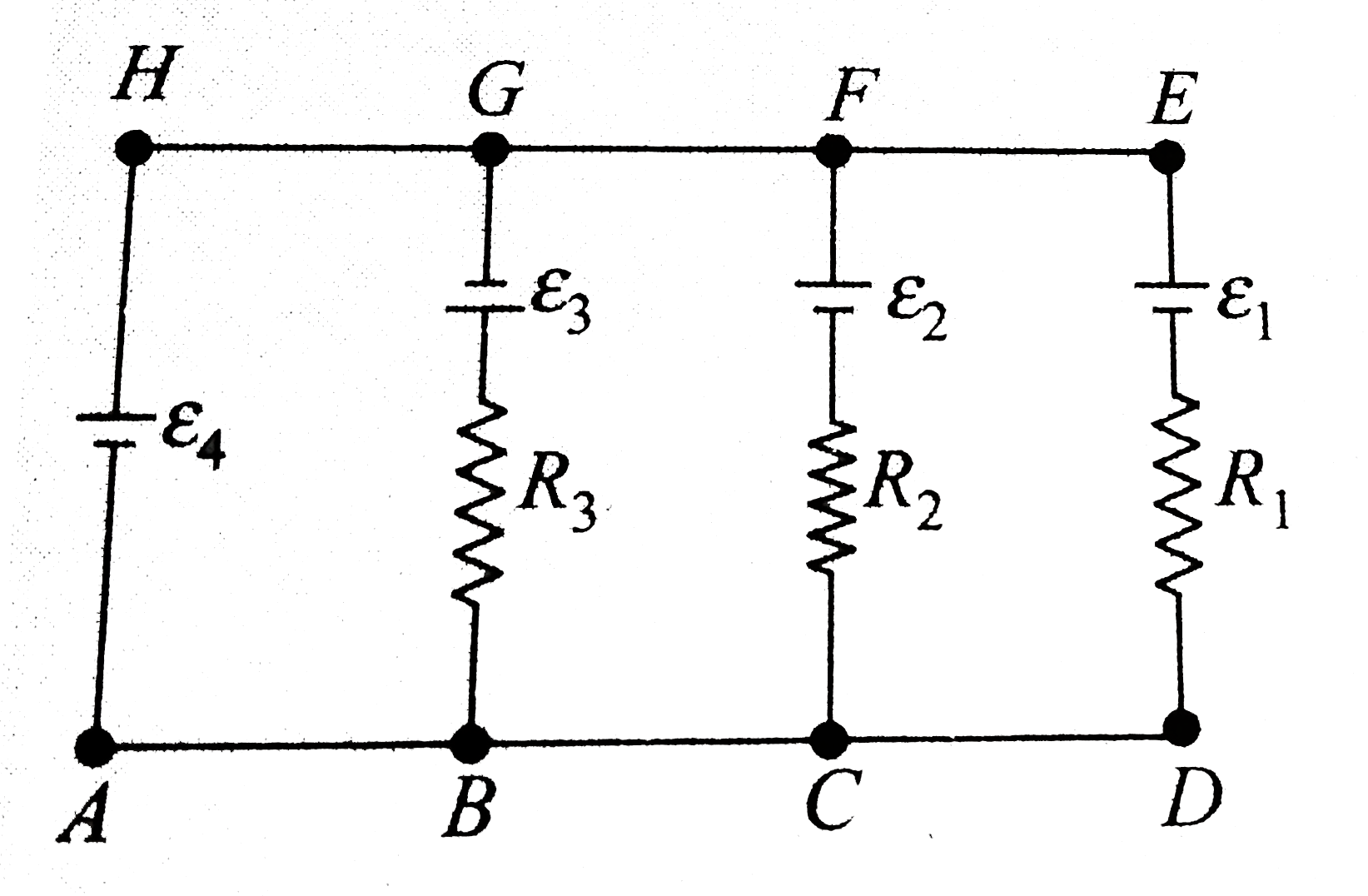
ε=50V,ε2=40V
ε3=30V,ε4=10V
R1=2Ω,R2=2Ω
R3=1ΩView SolutionFind the potential difference between the points a and b. If the points a and b are joined by a resistance of 5Ω, calculate the current through this resistance.
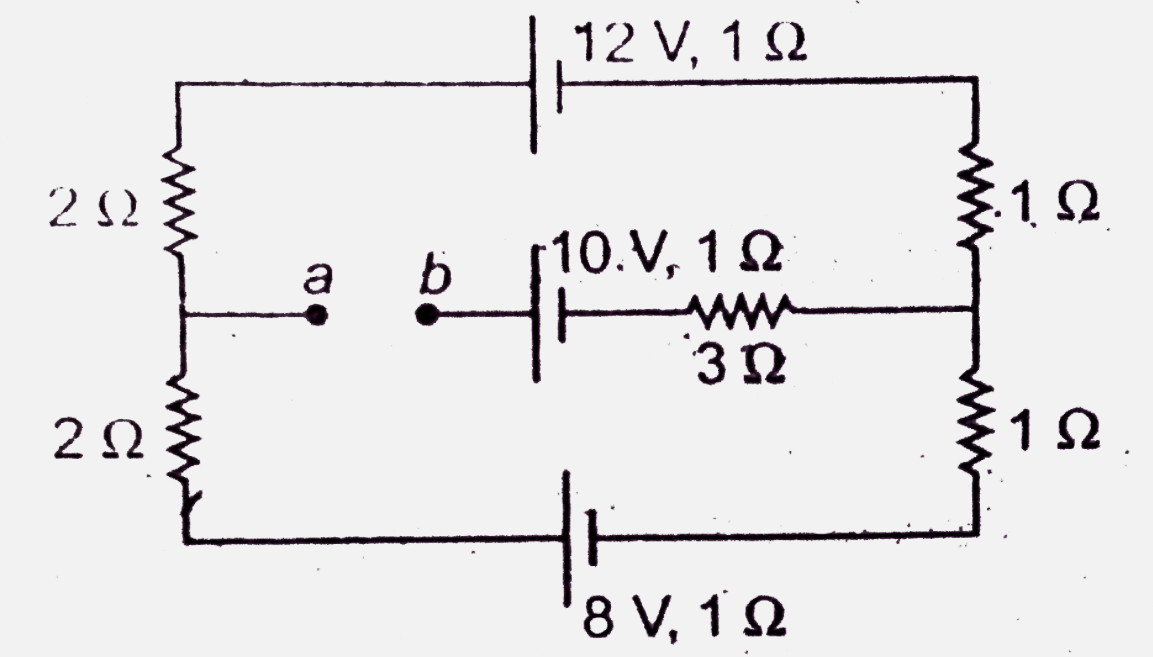 View Solution
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
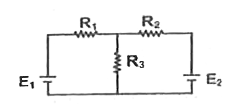 View Solution
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
 View Solution
View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Ω,andR3=4Ω. Find the currents i1andi2
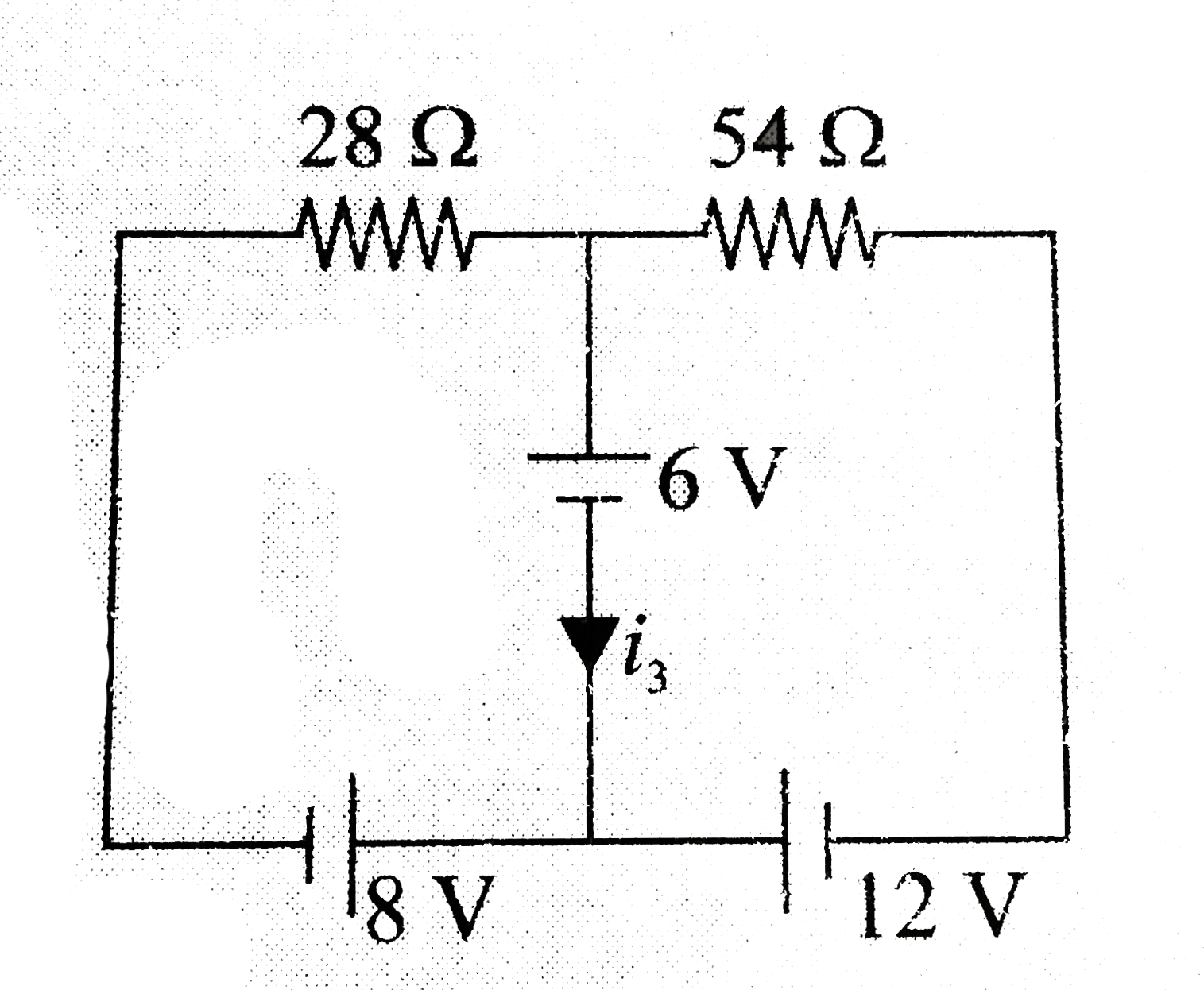 View Solution
View SolutionThe emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
View SolutionThe emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionIn the given circuit
E1=3E2=2E3= 6 volts R1=2R4=6Ω
R3=2R2=4Ω C=5μf.
Find the current in R and the energy stored in the capacitor.
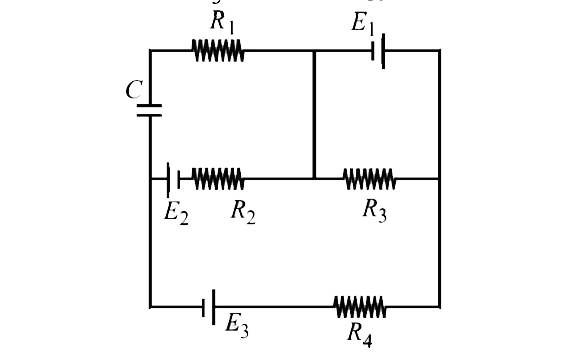 View Solution
View Solution

