The emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
E=1v r=1Ω
E=2v r=1Ω
E=2v,r=2Ω
E=2.5V, r=0.5Ω
To solve the problem, we need to find the EMF (ε) of the cell and its internal resistance (r) based on the given terminal potential differences (V) for different external resistances (R).
1. Identify the Given Values:
- For R1 = 4 Ω, V1 = 1.6 V
- For R2 = 9 Ω, V2 = 1.8 V
2. Use the Formula for Terminal Voltage:
The terminal voltage (V) can be expressed as:
V=ϵ−Ir
where I is the current flowing through the circuit. The current (I) can be calculated using Ohm's law:
I=VR
Therefore, we can rewrite the terminal voltage as:
V=ϵ−(VR)r
3. Set Up the Equations:
For the first condition (R1 = 4 Ω, V1 = 1.6 V):
1.6=ϵ−(1.64)r
Simplifying gives:
1.6=ϵ−0.4r(1)
For the second condition (R2 = 9 Ω, V2 = 1.8 V):
1.8=ϵ−(1.89)r
Simplifying gives:
1.8=ϵ−0.2r(2)
4. Equate the Two Equations:
From equations (1) and (2), we can express ε in terms of r:
ϵ=1.6+0.4r(from 1)
ϵ=1.8+0.2r(from 2)
Setting these equal to each other:
1.6+0.4r=1.8+0.2r
5. Solve for r:
Rearranging gives:
0.4r−0.2r=1.8−1.6
0.2r=0.2
r=1Ω
6. Substitute r back to find ε:
Substitute r = 1 Ω into equation (1):
ϵ=1.6+0.4(1)=1.6+0.4=2V
Final Results:
- EMF (ε) = 2 V
- Internal Resistance (r) = 1 Ω
- For R1 = 4 Ω, V1 = 1.6 V
- For R2 = 9 Ω, V2 = 1.8 V
The terminal voltage (V) can be expressed as:
V=ϵ−Ir
where I is the current flowing through the circuit. The current (I) can be calculated using Ohm's law:
I=VR
Therefore, we can rewrite the terminal voltage as:
V=ϵ−(VR)r
For the first condition (R1 = 4 Ω, V1 = 1.6 V):
1.6=ϵ−(1.64)r
Simplifying gives:
1.6=ϵ−0.4r(1)
1.8=ϵ−(1.89)r
Simplifying gives:
1.8=ϵ−0.2r(2)
From equations (1) and (2), we can express ε in terms of r:
ϵ=1.6+0.4r(from 1)
ϵ=1.8+0.2r(from 2)
1.6+0.4r=1.8+0.2r
Rearranging gives:
0.4r−0.2r=1.8−1.6
0.2r=0.2
r=1Ω
Substitute r = 1 Ω into equation (1):
ϵ=1.6+0.4(1)=1.6+0.4=2V
- EMF (ε) = 2 V
- Internal Resistance (r) = 1 Ω
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-3
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-4
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-1
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
The emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionA resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell is V. Write the expression for r in terms of ε, V and R.
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
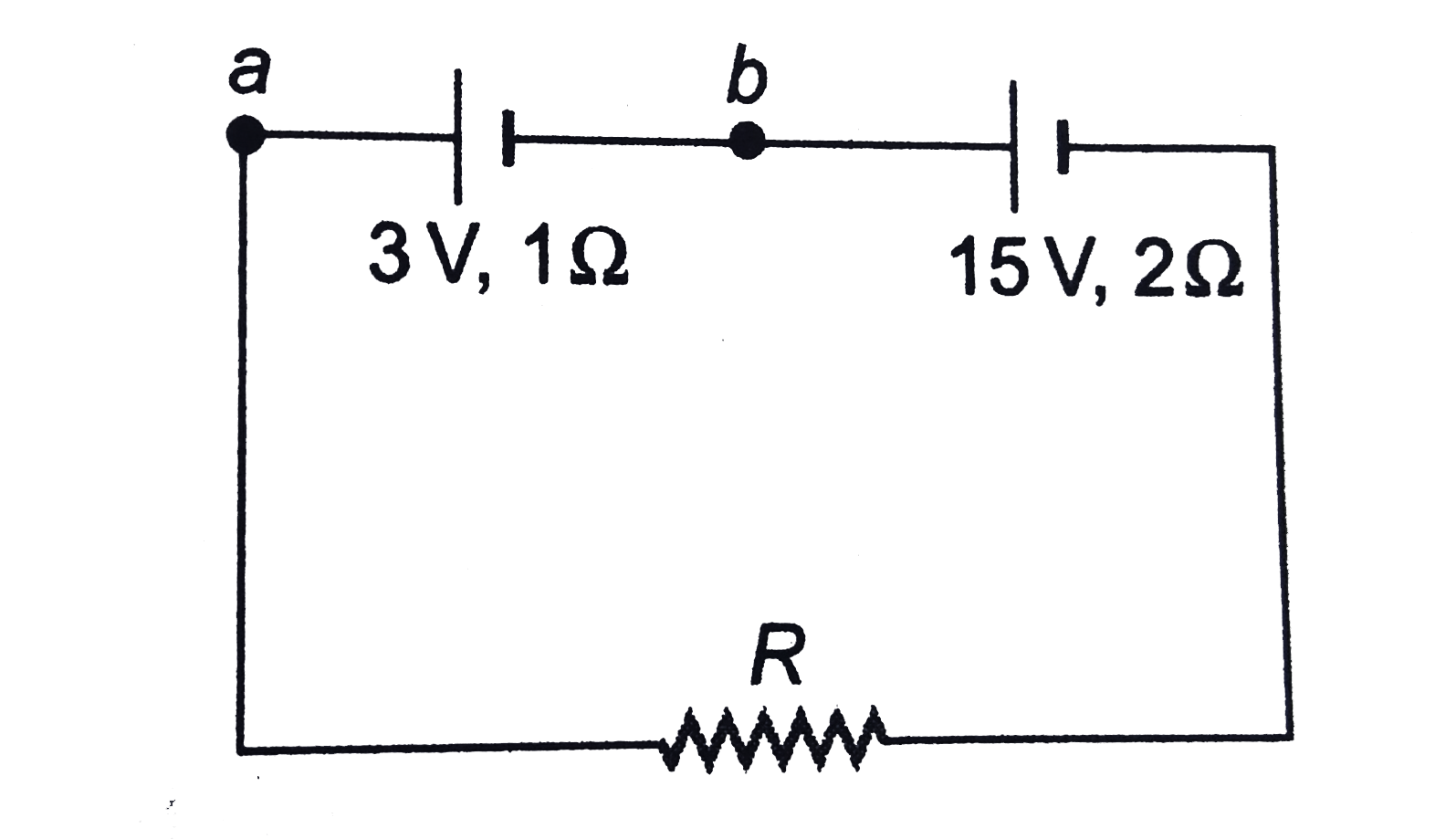
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View Solution
