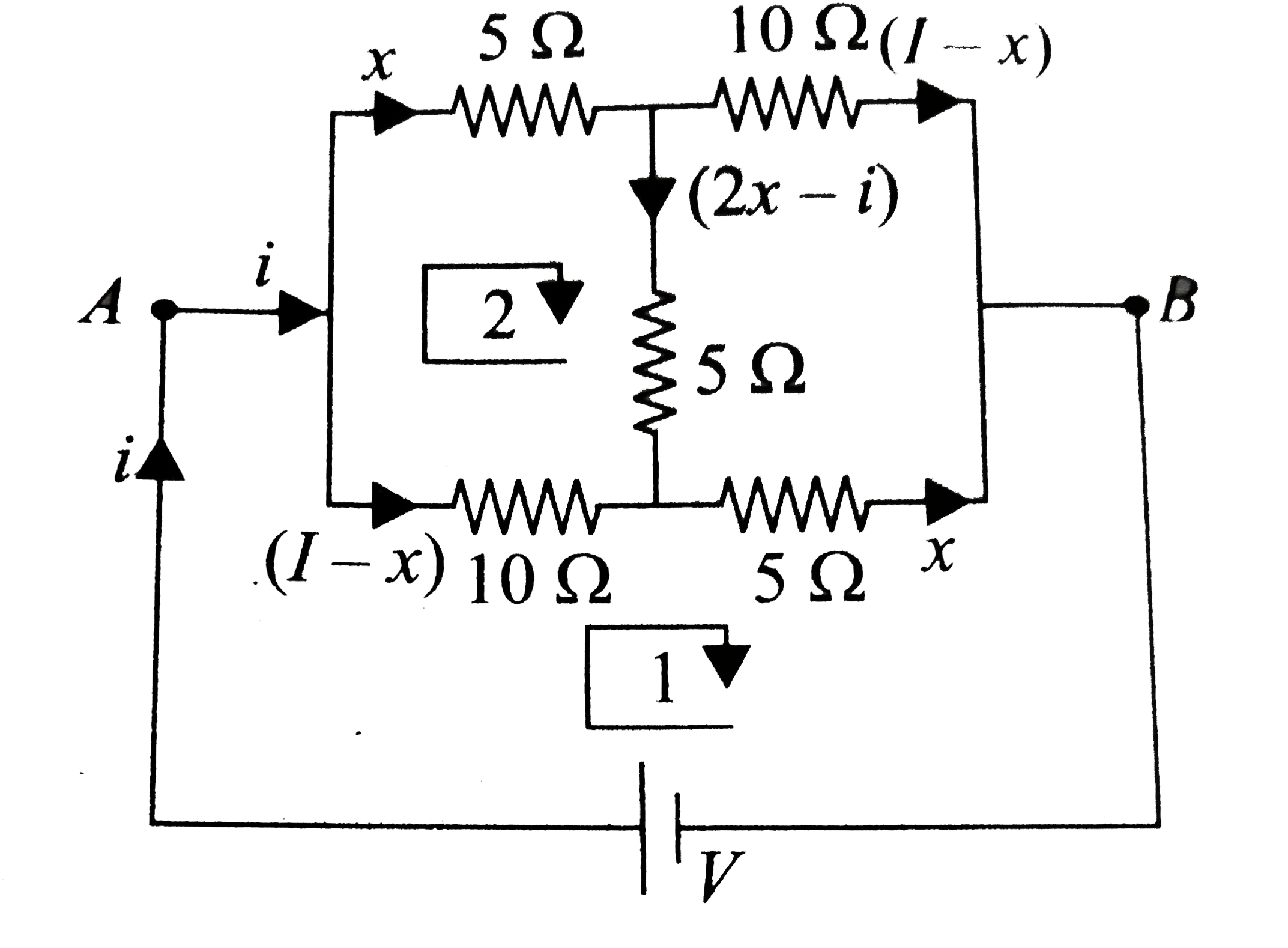
find the equivalent resistance between A and B. 
Method 1: it is a
wheatstone bridge, but it is
not balanced. There are no
series parallel connections.
But there are similar values
on input and output sides.
Here we see that even after
using symmetry, the circuit
does not reduce to series
parallel combiantion as in
previous examples. Therefore, we apply Kirchoff's voltage
law.
In loop 1 :
V−10(i−x)−5x=0
or V−10i+5x=0(i)
In loop2 : 10(i−x)−5x−5(2x−i)=0
or 10i−10x−10x+5i−5x=0
or 15i−25x=0
or x=1525i5x3i(ii)
Using (ii) and (i),
V−10i+3i=0
or VI=7ΩorReq=7Ω
Method 2: From shifted
symmetry, it is clear that the
current in the resistances
connected across nodes 1 and
2 will be same as the resistance
connected across nodes 5 and
4. Hence, potential differences
across these resistances will
be equal.
We can state the same for the resistances connected across
the nodes 6 and 5 and nodes 2 and 3. let us assingn the potentials
of points A and B to be V and 0, respectively, then we can
assign potentials of different nodes as shown in the figure. At
node 2
(x−V)5+(x−V−x)5+(x−0)10=0
orx=47V(i)
At point A, using Kirchhoff's junction rule
I=(V−x)5+[V−(V−x)]10=2V−x10(ii)
From (i) and (ii)
VI=7Ω=Req

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
The circuit diagram shwon in the fig consist of a large number of elementws (each element has two resistors R1andR2. The resistance of the resistors in each subsequent element differs by a factor of k=12 from the resistance of the resistors in previous elements find the equivalent resistance between A and B shown in
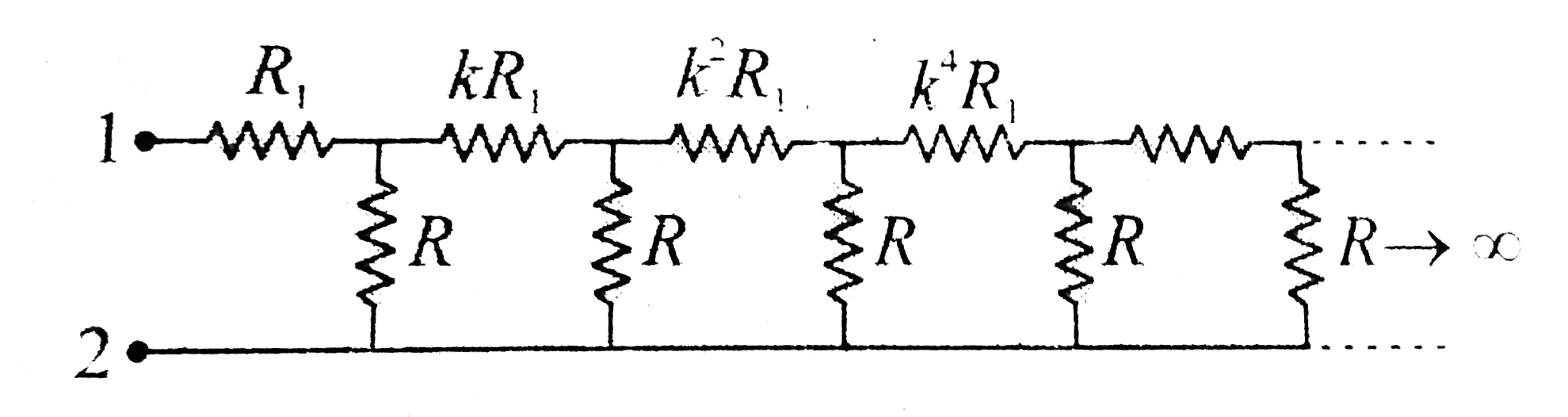 View Solution
View SolutionEquivalent resistance between A and B is
 View Solution
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
 View Solution
View SolutionFind equivalent resistance between A and B
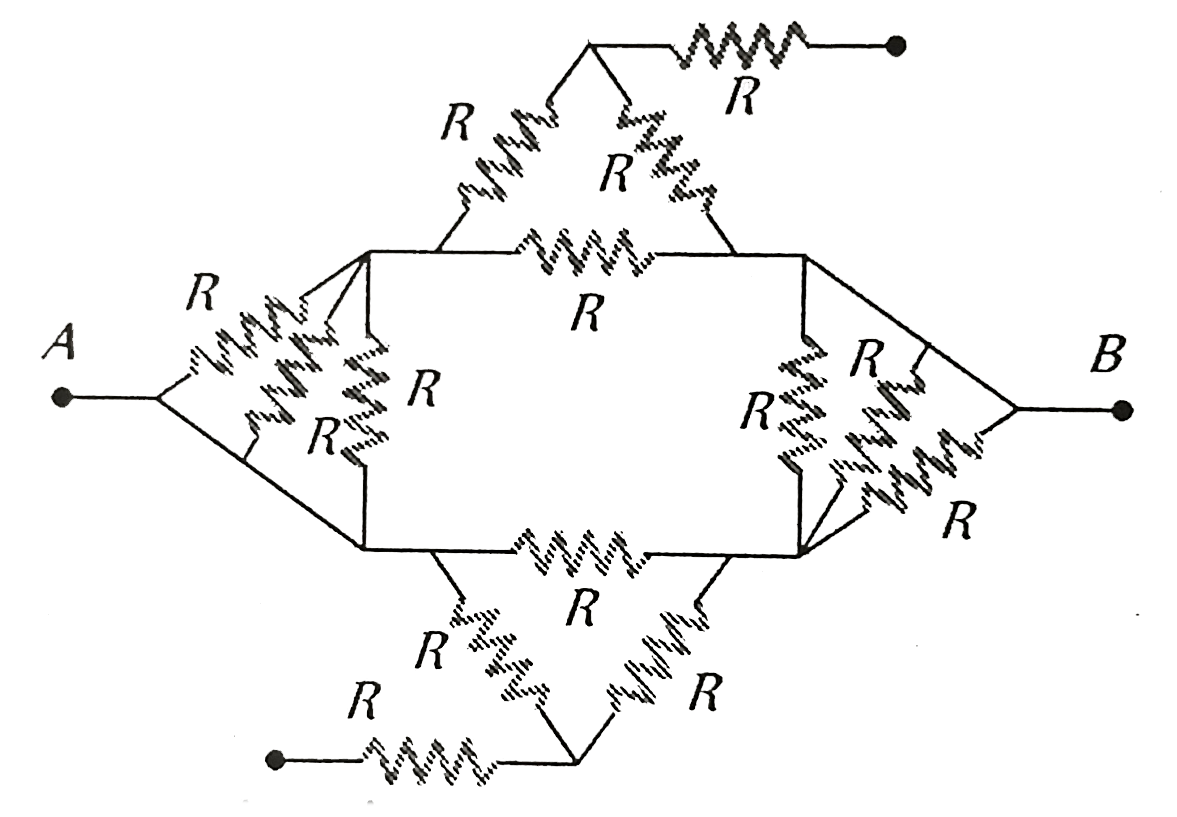 View Solution
View SolutionFind equivalent resistance between A and B
 View Solution
View SolutionFind equivalent resistance between A and B
 View Solution
View Solutionfind the equivalent resistance between A and E(resistance of each resistor is R.
 View Solution
View SolutionWhat is the equivalent resistance between A and B in the given circuit ?
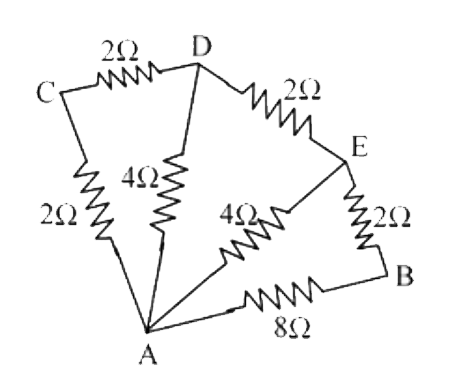 View Solution
View SolutionWhat is the equivalent resistance between A and B in the given circuit?
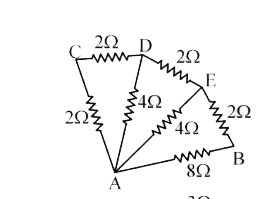 View Solution
View SolutionWhat is the equivalent resistance between A and B?
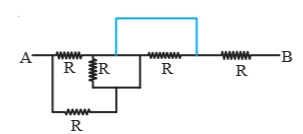 View Solution
View Solution
