A potential difference V is applied to copper wire of diameter d and length L, what will be the effect on, the electron drift speed by doubling (a) voltage V, (b) length L, and (c ) diameter d?
To solve the problem regarding the effect on electron drift speed when the voltage, length, and diameter of a copper wire are changed, we can follow these steps:
Step 1: Understanding the Drift Speed Formula
The drift speed vd of electrons in a conductor can be expressed as:
vd=eτm⋅E
where:
- e is the charge of the electron,
- τ is the relaxation time,
- m is the mass of the electron,
- E is the electric field.
Step 2: Relating Electric Field to Voltage and Length
The electric field E inside the wire can be defined as:
E=VL
where V is the potential difference and L is the length of the wire.
Step 3: Substituting Electric Field into Drift Speed Formula
Substituting the expression for electric field into the drift speed formula gives:
vd=eτm⋅VL
From this equation, we can see that:
- Drift speed vd is directly proportional to the voltage V.
- Drift speed vd is inversely proportional to the length L.
Step 4: Analyzing the Effects of Doubling Voltage V
If we double the voltage V (i.e., V→2V):
vd∝V⟹vd will also double.
Step 5: Analyzing the Effects of Doubling Length L
If we double the length L (i.e., L→2L):
vd∝1L⟹vd will become half.
Step 6: Analyzing the Effects of Doubling Diameter d
The drift speed vd is independent of the diameter d of the wire. Therefore, if we double the diameter d:
vd will not change.
Summary of Effects
1. Doubling Voltage V: Drift speed vd doubles.
2. Doubling Length L: Drift speed vd becomes half.
3. Doubling Diameter d: Drift speed vd remains unchanged.
The drift speed vd of electrons in a conductor can be expressed as:
vd=eτm⋅E
where:
- e is the charge of the electron,
- τ is the relaxation time,
- m is the mass of the electron,
- E is the electric field.
The electric field E inside the wire can be defined as:
E=VL
where V is the potential difference and L is the length of the wire.
Substituting the expression for electric field into the drift speed formula gives:
vd=eτm⋅VL
From this equation, we can see that:
- Drift speed vd is directly proportional to the voltage V.
- Drift speed vd is inversely proportional to the length L.
If we double the voltage V (i.e., V→2V):
vd∝V⟹vd will also double.
If we double the length L (i.e., L→2L):
vd∝1L⟹vd will become half.
The drift speed vd is independent of the diameter d of the wire. Therefore, if we double the diameter d:
vd will not change.
1. Doubling Voltage V: Drift speed vd doubles.
2. Doubling Length L: Drift speed vd becomes half.
3. Doubling Diameter d: Drift speed vd remains unchanged.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.2
Explore 50 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Subjective
Explore 29 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
A potential difference of 5V is applied across a conductor of length 10 cm. IF drift of electron is 2.5×10−4m/s, then electron mobility in SI unit is
View SolutionThe drift speed of electrons in copper wire of diameter and length l is v . If the potential difference across the wire is doubled, then the new drift speed becomes
View SolutionA potential difference of 5 V is applied across a conductor of length 10 cm . If drift velcoity of electrons is 2.5×10−4m/s , then electron mobility will be
View SolutionIf the potential difference between A and D is V, what will be potential difference between F and C. each of the resistance is R.
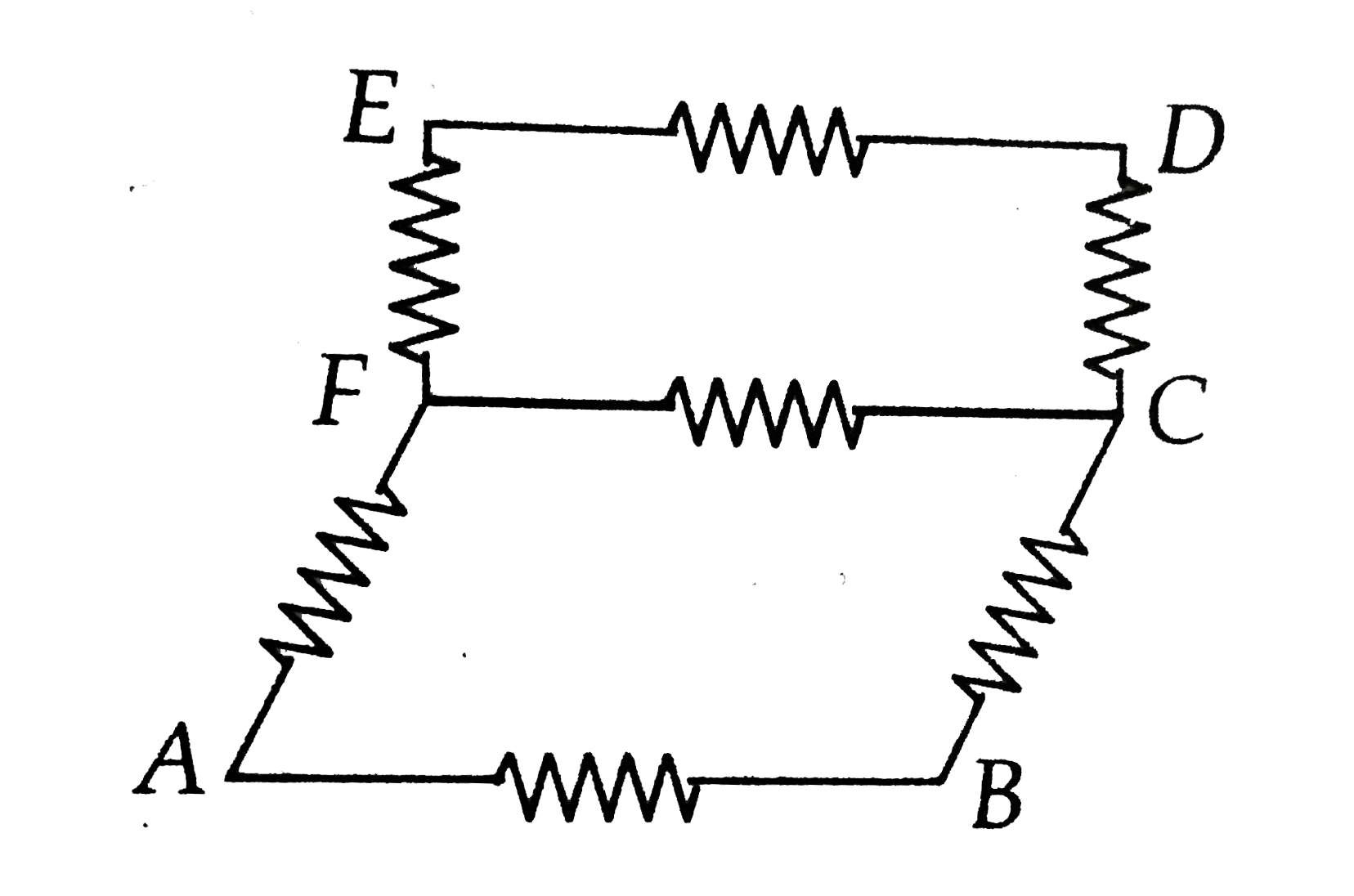
View SolutionA rectangular block of metal of resistivity p has dimensions d×2d×3d. A potential difference V is applied between two opposite faces of the block.
(a) To which two faces of the block should the potential difference V be applied to give the maximum current density? What is the maximum current density?
(b) To which two faces of the block should the potential difference V be applied to give the maximum current? What is this maximum current?
View SolutionA uniform wire of length L, diameter D and density ρ is stretched under a tension T. The correct relation between its fundamental frequency f, the length L and the diameter D is
View SolutionWhen 5 V potential difference is applied across a wire of length 0.1 m, the drift speed of electrons is 2.5×10−4ms−1. If the electron density in the wire is 8×1028m−3, the resistivity of the material is close to :
View SolutionA wire is replaced by another wire of same length and material but of twice diameter.
(i) What will be the effect on the increases in its length under a given load?
(ii) What will be the effect on the maximum load which it can bear?
View SolutionA : To a metal wire of diamete d and length L when the applied voltage is doubled, drift velocity gets doubled.
R : For a constant votage when the length is doubled, drift velocity will be halved but drift velocity is independent of diameter .
View SolutionA constant potential difference is applied across a metal wire. Let the average thermal velocity of electrons in the wire be vt and let the drift velocity be vd . As the temperature of the wire rises:
View Solution