A beam contains 2.0×108 doubly charged positive ions per cubic centimeter, all of which are moving toward north with a speed of 1.0×105ms−1. (a) what are the magnitude and direction of the current density →J? (b) can you calculate the total current i in this ion beam? If not what additional informaiton in needed.
To solve the problem step by step, we will address both parts of the question regarding the current density →J and the total current I.
Given Data:
- Number density of ions n=2.0×108 ions/cm³
- Speed of ions vd=1.0×105 m/s
- Each ion is doubly charged, so the charge q=2e where e=1.6×10−19 C.
Step 1: Convert the number density from cm³ to m³
To convert the number density from ions per cubic centimeter to ions per cubic meter:
n=2.0×108ions/cm3=2.0×108×106ions/m3=2.0×1014ions/m3
Step 2: Calculate the charge of each ion
Since the ions are doubly charged:
q=2e=2×1.6×10−19C=3.2×10−19C
Step 3: Calculate the current density →J
The formula for current density is given by:
→J=n⋅q⋅vd
Substituting the values:
→J=(2.0×1014ions/m3)⋅(3.2×10−19C)⋅(1.0×105m/s)
Calculating this gives:
→J=2.0×3.2×10−5A/m2=6.4×10−14A/m2
Thus, the magnitude of the current density is:
→J=6.4A/m2
Step 4: Determine the direction of →J
Since the ions are moving toward the north, the direction of the current density →J is also toward the north.
Answer for Part (a):
- Magnitude of current density →J: 6.4A/m2
- Direction of current density →J: North
Step 5: Calculate the total current I
The total current I can be calculated using the formula:
I=J⋅A
where A is the cross-sectional area of the beam.
Step 6: Identify the missing information
To calculate the total current I, we need the value of the cross-sectional area A of the beam.
Answer for Part (b):
- Can we calculate the total current I?: No, we need the cross-sectional area A of the ion beam.
Summary of the Solution:
1. Converted number density to m³.
2. Calculated the charge of each doubly charged ion.
3. Used the formula for current density to find →J.
4. Determined the direction of →J.
5. Identified that the cross-sectional area is needed to calculate the total current.
- Number density of ions n=2.0×108 ions/cm³
- Speed of ions vd=1.0×105 m/s
- Each ion is doubly charged, so the charge q=2e where e=1.6×10−19 C.
To convert the number density from ions per cubic centimeter to ions per cubic meter:
n=2.0×108ions/cm3=2.0×108×106ions/m3=2.0×1014ions/m3
Since the ions are doubly charged:
q=2e=2×1.6×10−19C=3.2×10−19C
The formula for current density is given by:
→J=n⋅q⋅vd
Substituting the values:
→J=(2.0×1014ions/m3)⋅(3.2×10−19C)⋅(1.0×105m/s)
Calculating this gives:
→J=2.0×3.2×10−5A/m2=6.4×10−14A/m2
Thus, the magnitude of the current density is:
→J=6.4A/m2
Since the ions are moving toward the north, the direction of the current density →J is also toward the north.
- Magnitude of current density →J: 6.4A/m2
- Direction of current density →J: North
The total current I can be calculated using the formula:
I=J⋅A
where A is the cross-sectional area of the beam.
To calculate the total current I, we need the value of the cross-sectional area A of the beam.
- Can we calculate the total current I?: No, we need the cross-sectional area A of the ion beam.
1. Converted number density to m³.
2. Calculated the charge of each doubly charged ion.
3. Used the formula for current density to find →J.
4. Determined the direction of →J.
5. Identified that the cross-sectional area is needed to calculate the total current.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.2
50 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
The electrons in a particle beam each have a kinetic energy of 1.6×10−17J. What are the magnitude and direction of the electric field that stops these electrons in a distance of 10.0cm
View SolutionAn electorn moves in a circle of radius 10cm with a constant speed of 4.0×106ms−1.Find the electric current at a point on the circle.
View SolutionTwo fixed long parallel horizontal rails, a distance 1 m apart are joined at one end by a resistance 1Ω. A rod AB of negligible resistance slides towards the resistance. A magnetic field of magnitude 4T perpendicular to the plane of rails exists. Find the current flowing (in Ampere) in the resistance, at an instant when the velocity of the rod is 2 m/s.
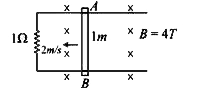
View SolutionA straight conductor carries a current of 5A. An electron travelling with a speed of 5×106ms−1 parallel to the wire at a distance of 0.1m from the conductor, experiences a force of
View SolutionAn electron beam has an aperture of 2mm2. A total of 7×1016 electrons flow through any perpendicular cross-section per second. Calculate the current density in the electron beam.
View SolutionAn electron has a speed 3×102ms−1 with uncertainty 0.07% what is the uncertainty in locating its position ?
View SolutionThe electron with change (q=1.6×10−19C) moves in an orbit of radius 5×10−11m with a speed of 2.2×106ms−1, around an atom. The equivalent current is
View SolutionAn α - particle with a specific charge of 2.5×107Ckg−1 moves with a speed of 2×105ms−1 in a perpendicular magnetic field of 0.05T. Then , the radius of the circular path described by it is
View SolutionAn electorn beam has an aperture 1.0mm2. A totak of 6.0×1016 electons go through any perpendicular cross section per second. Find(a) the current and (b) the current density in the beam.
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View Solution
