In which of the follwing arrangements of resistors does the meter M, which has a resistance of 2Ω, give the largest reading when the same potential difference is appliced between points P and Q?


The correct Answer is:C
To determine in which arrangement of resistors the meter M (with a resistance of 2Ω) gives the largest reading when the same potential difference is applied between points P and Q, we will analyze each arrangement step by step.
1. Understanding the Problem:
We need to find the arrangement of resistors that allows the maximum current to flow through the meter M when a potential difference (voltage) is applied across points P and Q.
2. Analyzing Arrangement A:
- In Arrangement A, assume we have resistors of 1Ω, 1Ω, and the meter M of 2Ω in series.
- The total resistance \( R_A = 1 + 1 + 2 = 4 \, \Omega \).
- The current \( I_A = \frac{V_{PQ}}{R_A} = \frac{V_{PQ}}{4} \).
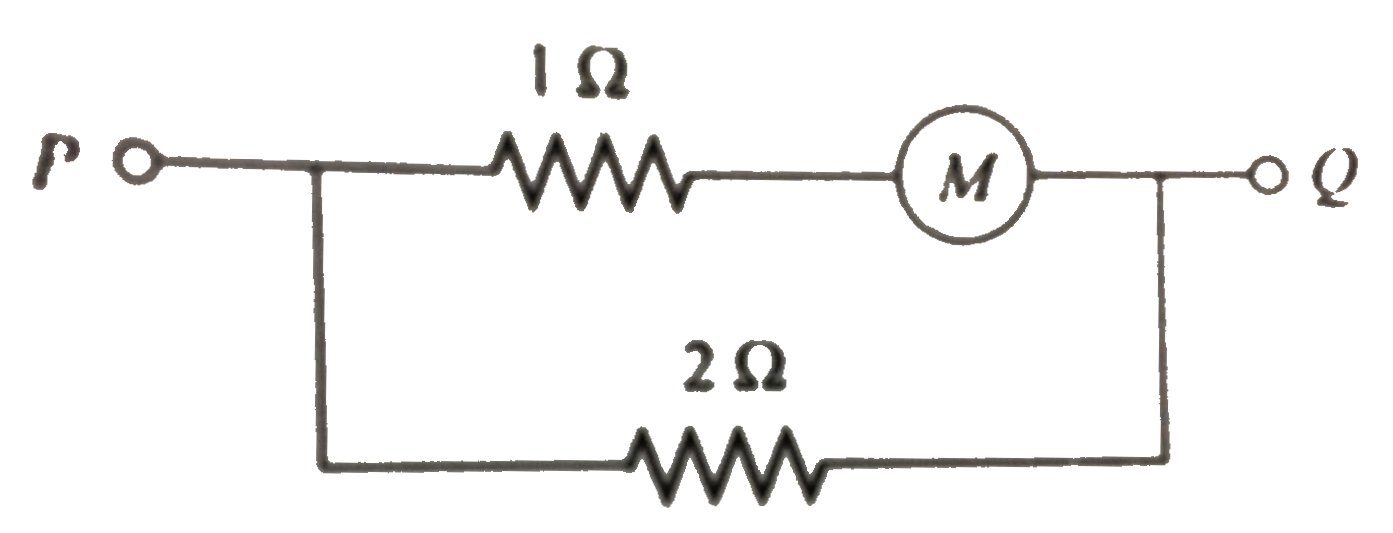
3. Analyzing Arrangement B:
- In Arrangement B, we have two resistors of 1Ω and 2Ω in parallel, and the meter M in series.
- The equivalent resistance of the parallel resistors \( R_{parallel} = \frac{1 \cdot 2}{1 + 2} = \frac{2}{3} \, \Omega \).
- The total resistance \( R_B = R_{parallel} + R_M = \frac{2}{3} + 2 = \frac{8}{3} \, \Omega \).
- The current \( I_B = \frac{V_{PQ}}{R_B} = \frac{V_{PQ}}{\frac{8}{3}} = \frac{3V_{PQ}}{8} \).
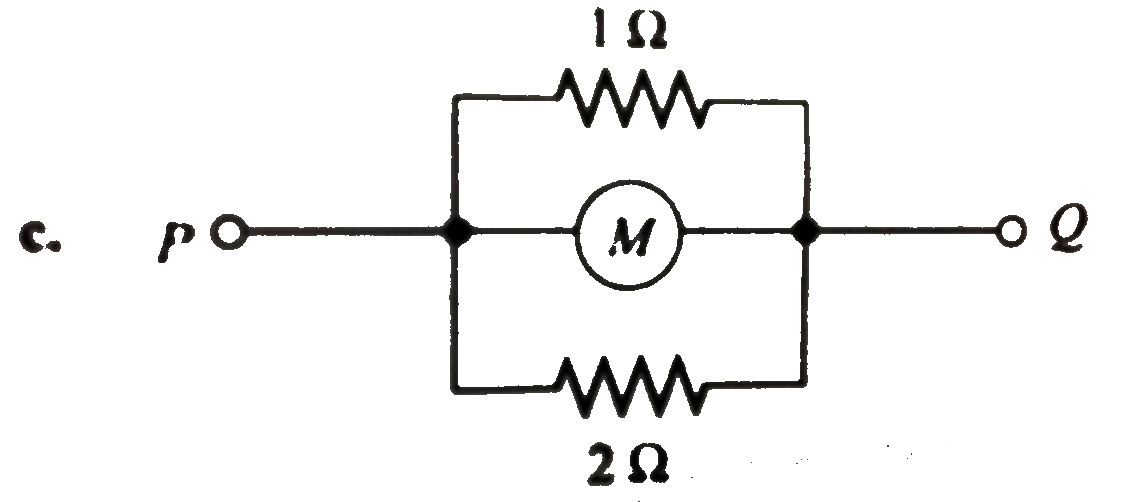
4. Analyzing Arrangement C:
- In Arrangement C, the meter M is in parallel with two resistors of 1Ω each.
- The equivalent resistance of the two 1Ω resistors in parallel \( R_{parallel} = \frac{1 \cdot 1}{1 + 1} = \frac{1}{2} \, \Omega \).
- The total resistance \( R_C = \frac{1}{2} \, \Omega \) (since the meter is in parallel).
- The current \( I_C = \frac{V_{PQ}}{R_C} = \frac{V_{PQ}}{\frac{1}{2}} = 2V_{PQ} \).
5. Analyzing Arrangement D:
- In Arrangement D, we have resistors of 1Ω and 2Ω in series with the meter M.
- The total resistance \( R_D = 1 + 2 + 2 = 5 \, \Omega \).
- The current \( I_D = \frac{V_{PQ}}{R_D} = \frac{V_{PQ}}{5} \).
6. Comparing the Currents:
- \( I_A = \frac{V_{PQ}}{4} \)
- \( I_B = \frac{3V_{PQ}}{8} \)
- \( I_C = 2V_{PQ} \)
- \( I_D = \frac{V_{PQ}}{5} \)
7. Finding the Maximum Current:
- Among the calculated currents, \( I_C = 2V_{PQ} \) is the largest current.
- Therefore, the arrangement that gives the largest reading on the meter M is Arrangement C.
Conclusion:
The arrangement of resistors that allows the meter M to give the largest reading is Arrangement C.
We need to find the arrangement of resistors that allows the maximum current to flow through the meter M when a potential difference (voltage) is applied across points P and Q.
- In Arrangement A, assume we have resistors of 1Ω, 1Ω, and the meter M of 2Ω in series.
- The total resistance \( R_A = 1 + 1 + 2 = 4 \, \Omega \).
- The current \( I_A = \frac{V_{PQ}}{R_A} = \frac{V_{PQ}}{4} \).
- In Arrangement B, we have two resistors of 1Ω and 2Ω in parallel, and the meter M in series.
- The equivalent resistance of the parallel resistors \( R_{parallel} = \frac{1 \cdot 2}{1 + 2} = \frac{2}{3} \, \Omega \).
- The total resistance \( R_B = R_{parallel} + R_M = \frac{2}{3} + 2 = \frac{8}{3} \, \Omega \).
- The current \( I_B = \frac{V_{PQ}}{R_B} = \frac{V_{PQ}}{\frac{8}{3}} = \frac{3V_{PQ}}{8} \).
- In Arrangement C, the meter M is in parallel with two resistors of 1Ω each.
- The equivalent resistance of the two 1Ω resistors in parallel \( R_{parallel} = \frac{1 \cdot 1}{1 + 1} = \frac{1}{2} \, \Omega \).
- The total resistance \( R_C = \frac{1}{2} \, \Omega \) (since the meter is in parallel).
- The current \( I_C = \frac{V_{PQ}}{R_C} = \frac{V_{PQ}}{\frac{1}{2}} = 2V_{PQ} \).
- In Arrangement D, we have resistors of 1Ω and 2Ω in series with the meter M.
- The total resistance \( R_D = 1 + 2 + 2 = 5 \, \Omega \).
- The current \( I_D = \frac{V_{PQ}}{R_D} = \frac{V_{PQ}}{5} \).
- \( I_A = \frac{V_{PQ}}{4} \)
- \( I_B = \frac{3V_{PQ}}{8} \)
- \( I_C = 2V_{PQ} \)
- \( I_D = \frac{V_{PQ}}{5} \)
- Among the calculated currents, \( I_C = 2V_{PQ} \) is the largest current.
- Therefore, the arrangement that gives the largest reading on the meter M is Arrangement C.
The arrangement of resistors that allows the meter M to give the largest reading is Arrangement C.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct7videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Assertion-Reasoning7videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Subjective18videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type7videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Calculate the amount of charge flowing in 2 minutes in a wire of resistance 10Ω when a potential difference of 20 V is applied between its ends
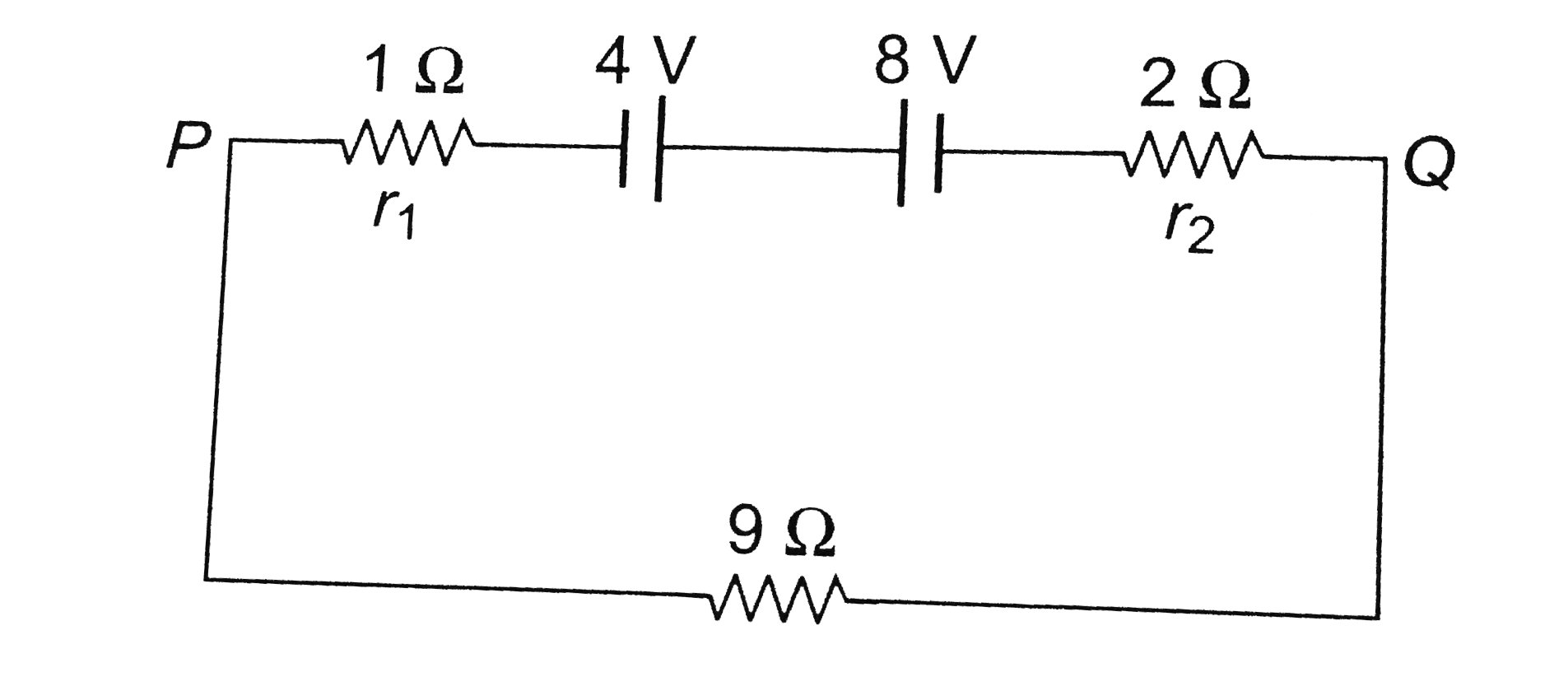
View SolutionTwo batteries of e.m.f. 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Which arrangement of 3Ω resistors will give a total resistance of 7Ω?
A B
B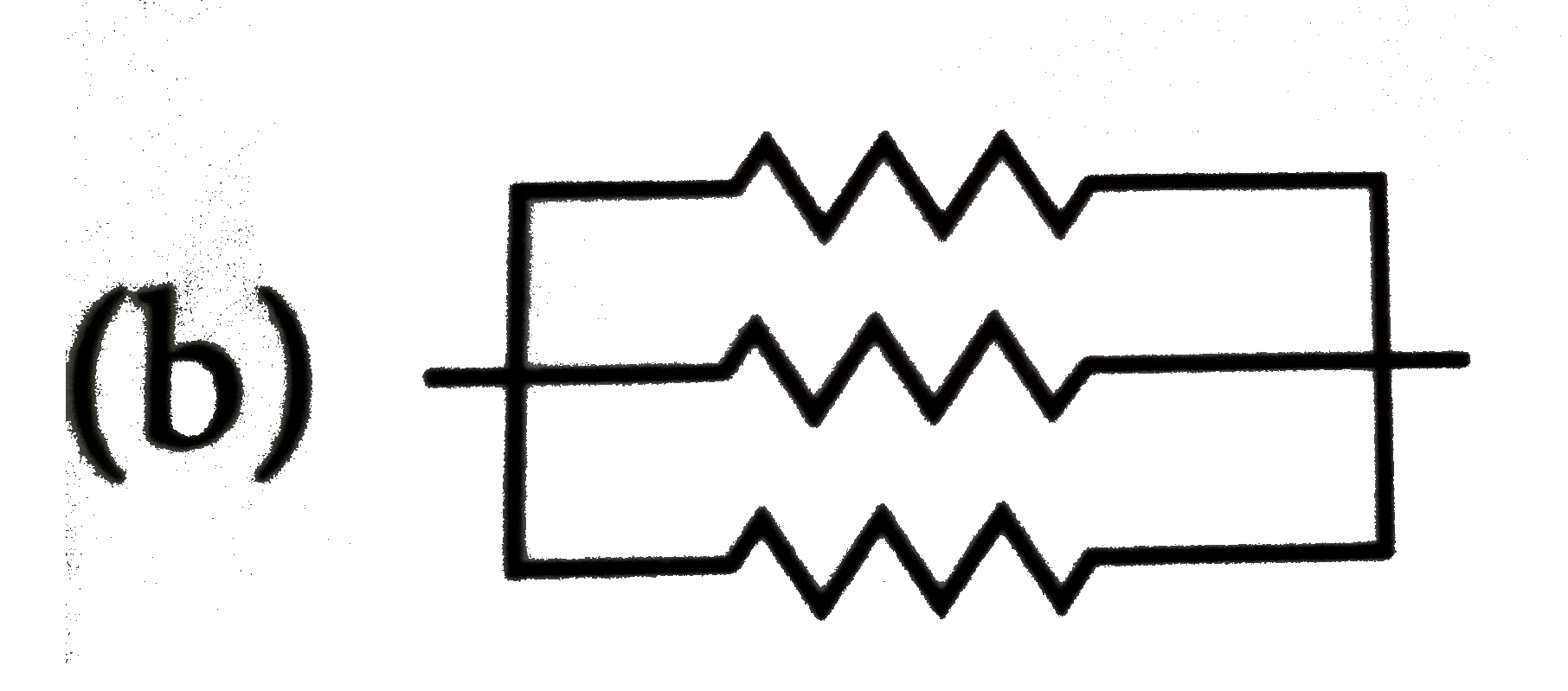 C
C D
D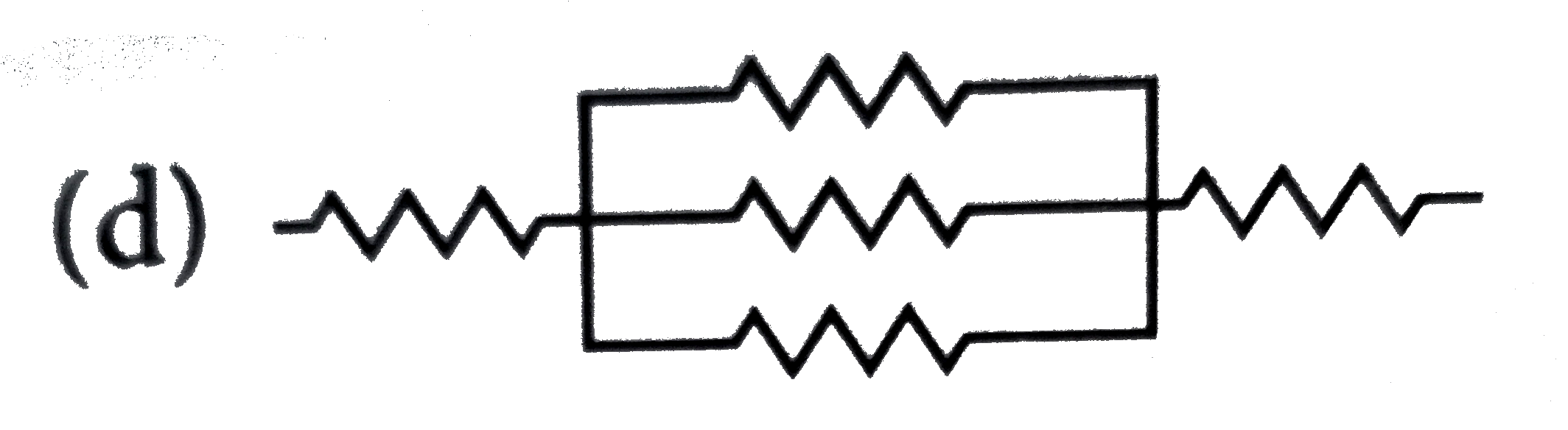
Two batteries of emf 4 V and 8 V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q are
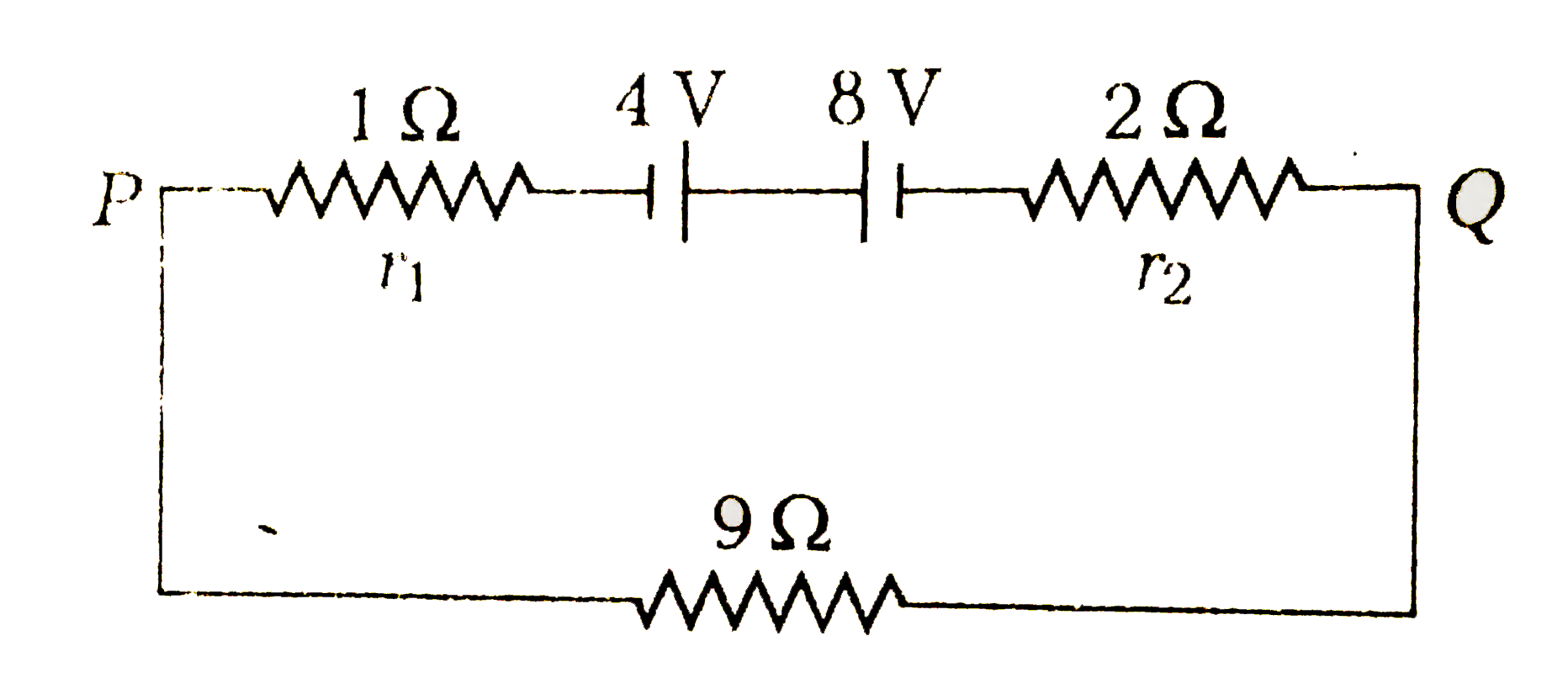 View Solution
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
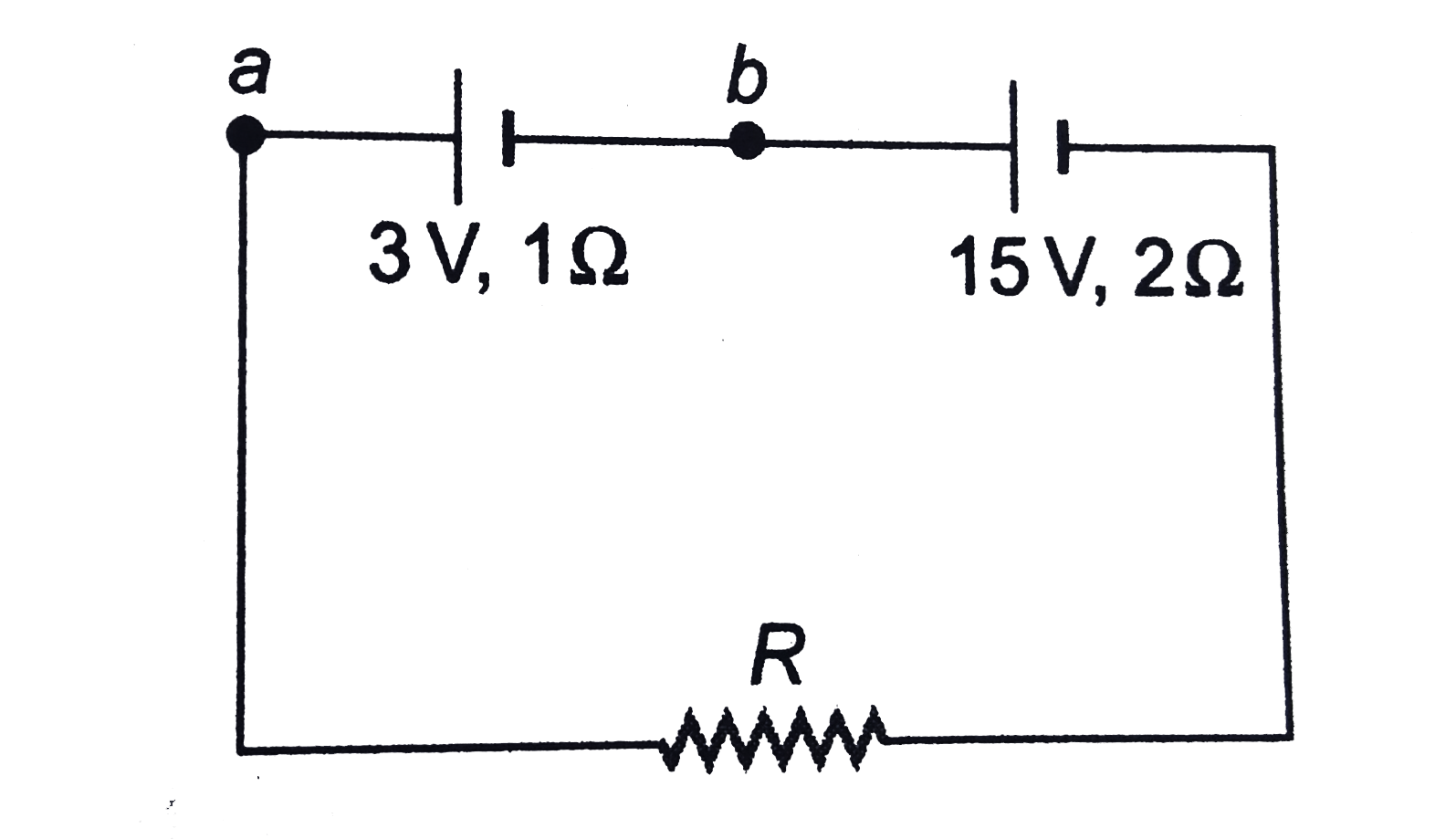 View Solution
View SolutionP,Q is a uniform wire of resistance 2000Ω and M is the md point of PQ. A voltmeter of resistance 1000Ω is connected between P and M. the reading of the voltmeter, when, the potential differences applied between PQ is 150volt will be
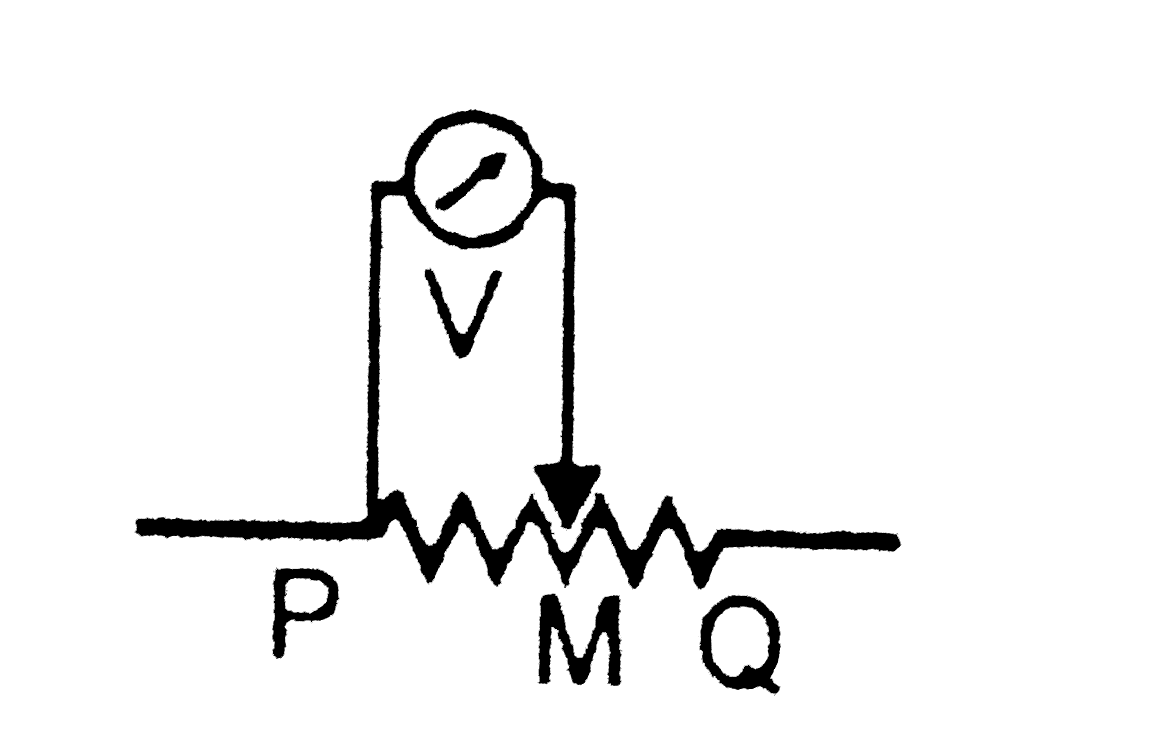 View Solution
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
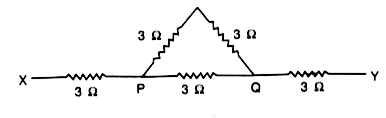 View Solution
View SolutionConsider the circuit shown below where all resistors are of 1kΩ
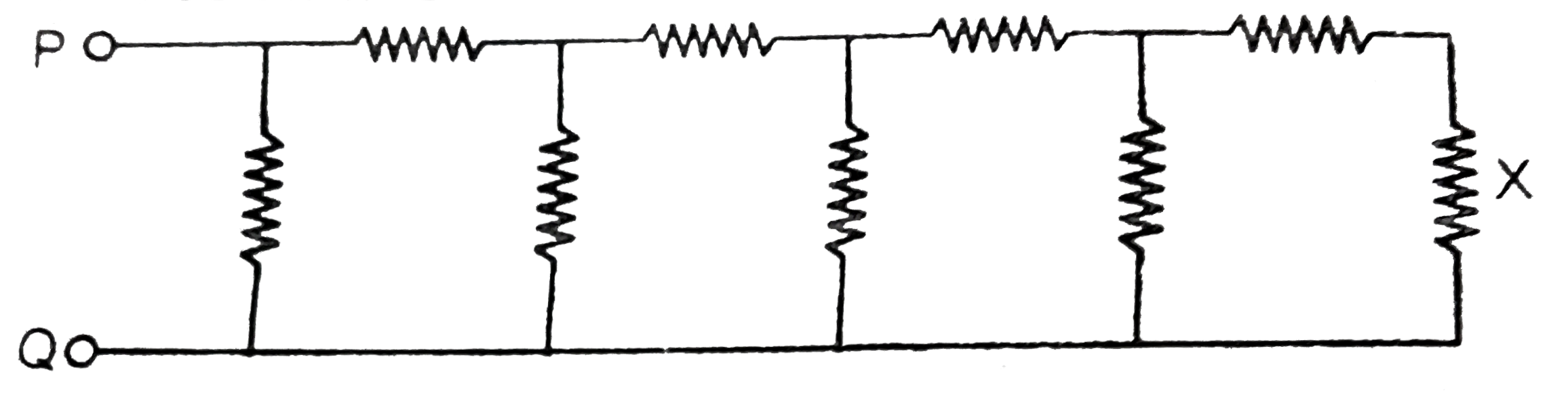
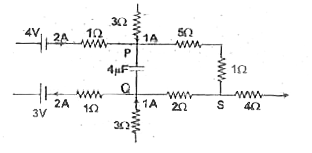
If a current of magnitude 1 mA flows through the resistor marked X, what is the potential difference measured between point P and Q ?View SolutionA part of a circuit in steady state with the currents flowing in a braches , the value of resistance etc is shown in the figure.
Potential difference between points P and Q.isView SolutionA resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
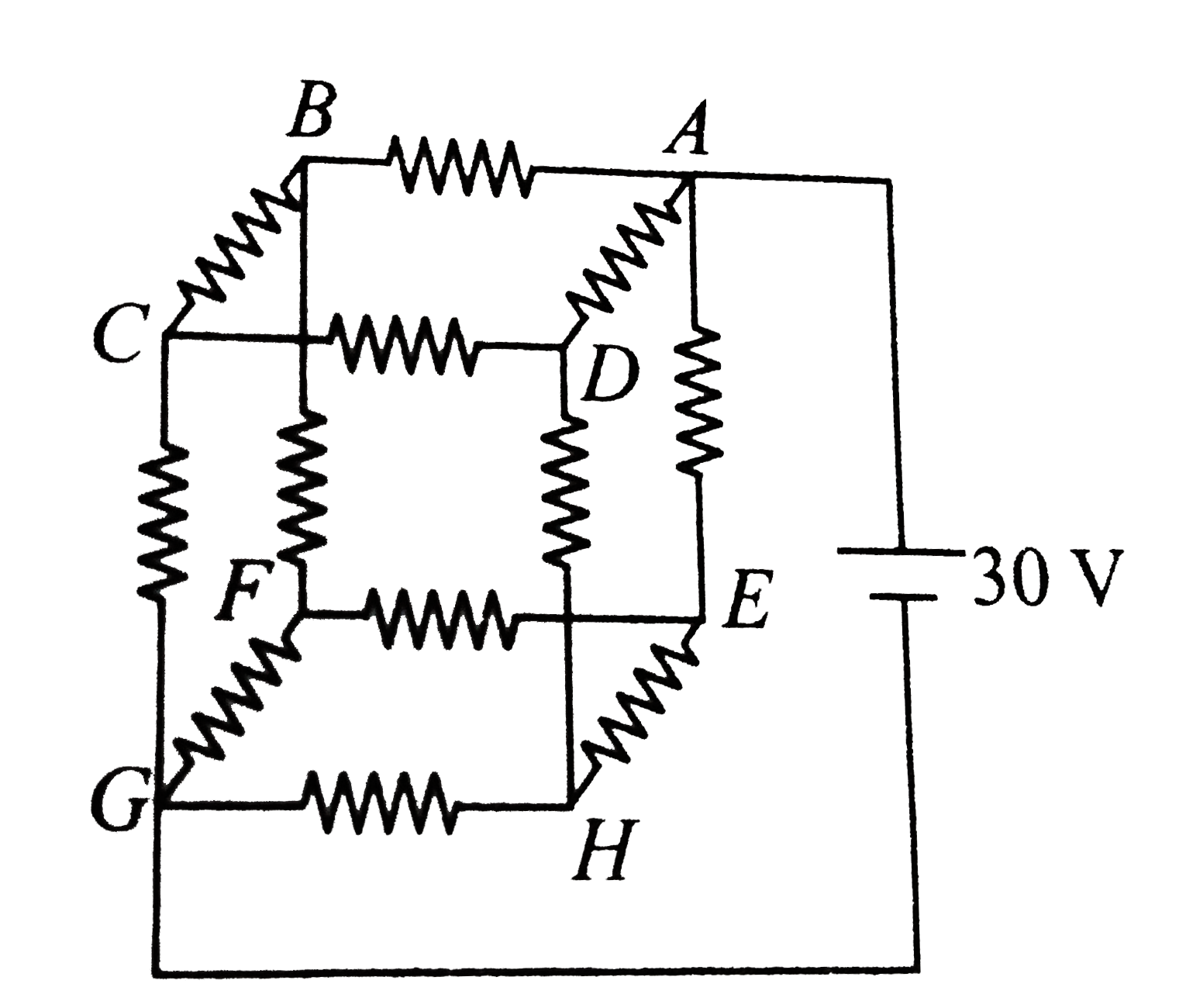
In question 20, the potential difference between the points C and G isView Solution

