Consider a wheatstone bridge PQRS as shown in Fig. 7.19wherecurrentIis∈the∘uitoffourresistances10,20,30,and40Ω.F∈dtheratiooftheheat≥≠rated∈thefourarmsPQ,QR, PS, and SR.
To solve the problem of finding the ratio of heat generated in the four arms of the Wheatstone bridge PQRS, we will follow these steps:
Step 1: Identify the resistances
The resistances in the Wheatstone bridge are given as follows:
- RPQ=10Ω
- RQR=20Ω
- RPS=30Ω
- RSR=40Ω
Step 2: Check if the Wheatstone bridge is balanced
To check if the Wheatstone bridge is balanced, we use the condition:
RPQRQR=RPSRSR
Calculating the ratios:
1020=12and3040=34
Since the ratios are not equal, the bridge is not balanced.
Step 3: Determine the current distribution
In a Wheatstone bridge, if it is not balanced, the current will split at junction P. Let I1 be the current through PQ and I2 be the current through PS. The total current I entering the junction P is given by:
I=I1+I2
Step 4: Apply Kirchhoff's laws to find current values
Using Kirchhoff's laws, we can set up equations based on the potential differences across the resistances. The potential drop across each resistance can be expressed as:
- For PQ: I1⋅10
- For QR: I1⋅20
- For PS: I2⋅30
- For SR: I2⋅40
Setting up the equations:
1. I1⋅10+I2⋅30=I1⋅20 (from the loop PQRS)
2. I1⋅20=I2⋅40 (from the loop QSR)
From equation 2, we can express I2 in terms of I1:
I2=I1⋅2040=I12
Step 5: Substitute I2 back into the first equation
Substituting I2 into the first equation:
I1⋅10+(I12)⋅30=I1⋅20
Simplifying this gives:
10I1+15I1=20I1
This confirms that our current distribution is consistent.
Step 6: Calculate the heat generated in each arm
Using the formula for heat generated H=I2Rt (where t is time, which we can assume to be constant for ratio calculations), we can express the heat generated in each arm as:
- Heat in PQ: HPQ=I21⋅10
- Heat in QR: HQR=I21⋅20
- Heat in PS: HPS=I22⋅30=(I12)2⋅30=I214⋅30=30I214=7.5I21
- Heat in SR: HSR=I22⋅40=(I12)2⋅40=I214⋅40=40I214=10I21
Step 7: Find the ratio of heat generated
Now we can find the ratio of heat generated in each arm:
HPQ:HQR:HPS:HSR=(10I21):(20I21):(7.5I21):(10I21)
This simplifies to:
10:20:7.5:10
Dividing all terms by 2.5 gives:
4:8:3:4
Final Answer
Thus, the ratio of the heat generated in the four arms PQ,QR,PS, and SR is:
4:8:3:4
The resistances in the Wheatstone bridge are given as follows:
- RPQ=10Ω
- RQR=20Ω
- RPS=30Ω
- RSR=40Ω
To check if the Wheatstone bridge is balanced, we use the condition:
RPQRQR=RPSRSR
Calculating the ratios:
1020=12and3040=34
Since the ratios are not equal, the bridge is not balanced.
In a Wheatstone bridge, if it is not balanced, the current will split at junction P. Let I1 be the current through PQ and I2 be the current through PS. The total current I entering the junction P is given by:
I=I1+I2
Using Kirchhoff's laws, we can set up equations based on the potential differences across the resistances. The potential drop across each resistance can be expressed as:
- For PQ: I1⋅10
- For QR: I1⋅20
- For PS: I2⋅30
- For SR: I2⋅40
1. I1⋅10+I2⋅30=I1⋅20 (from the loop PQRS)
2. I1⋅20=I2⋅40 (from the loop QSR)
I2=I1⋅2040=I12
Substituting I2 into the first equation:
I1⋅10+(I12)⋅30=I1⋅20
Simplifying this gives:
10I1+15I1=20I1
This confirms that our current distribution is consistent.
Using the formula for heat generated H=I2Rt (where t is time, which we can assume to be constant for ratio calculations), we can express the heat generated in each arm as:
- Heat in PQ: HPQ=I21⋅10
- Heat in QR: HQR=I21⋅20
- Heat in PS: HPS=I22⋅30=(I12)2⋅30=I214⋅30=30I214=7.5I21
- Heat in SR: HSR=I22⋅40=(I12)2⋅40=I214⋅40=40I214=10I21
Now we can find the ratio of heat generated in each arm:
HPQ:HQR:HPS:HSR=(10I21):(20I21):(7.5I21):(10I21)
This simplifies to:
10:20:7.5:10
Dividing all terms by 2.5 gives:
4:8:3:4
Thus, the ratio of the heat generated in the four arms PQ,QR,PS, and SR is:
4:8:3:4
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.122videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective8videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
A copper voltameter is connected in series with a coil of resistance 100Ω. A steady current flowing in the circuit for 10 minutes, gives a deposit of 0.1 g of copper in the voltameter. Calculate the heat generated in the resistance coil. (ECE of Cu3.3×10−7kg/C)
View SolutionThe resistance of the four arms A, B, C and D of a wheatstone bridge as shown in the figure are 10Ω, 20Ω ,30Ω and 60Ω respectively . The emf and internal resistance of the cell are 15V and 2.5Ω respectively . If the galvanometer resistance is 80Ω then the net current drawn from the cell will be
_PHY_E05_111_Q01.png) View Solution
View SolutionConsider the circuit shown in the figure. Find the current in branch AO and OC . Potential of point A = 10 V of point B = 20 V and of C = 30 V.
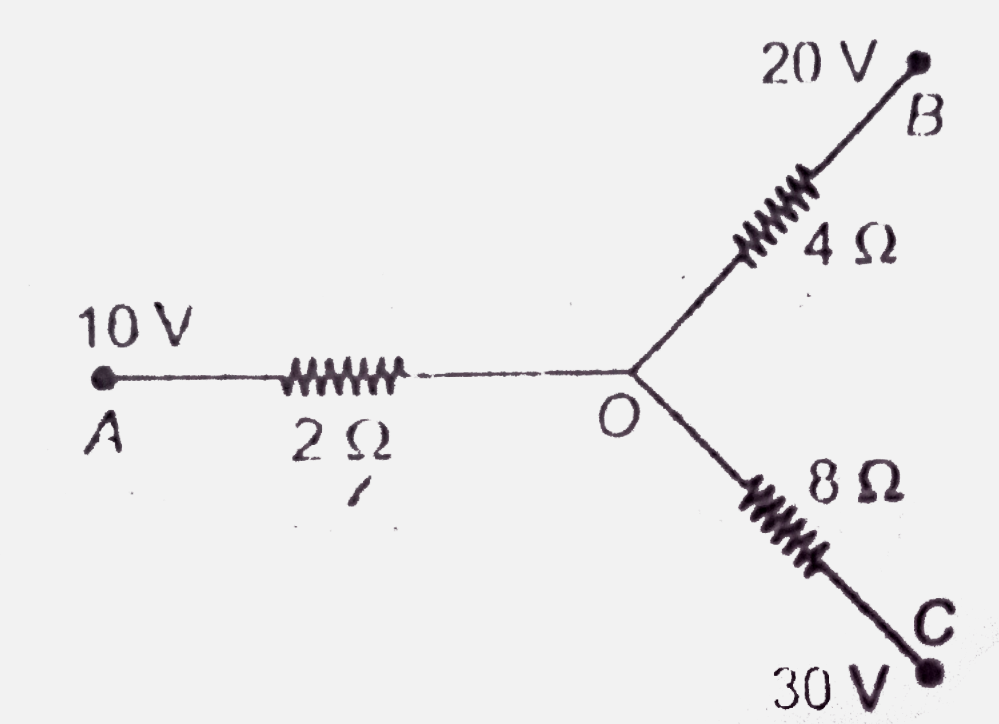 View Solution
View SolutionConsider the circuit shown in fig 5.168. Find out the steady - state current in the 4Ω resistor. Assume the internal resistance of 8 V battery to be negligible.
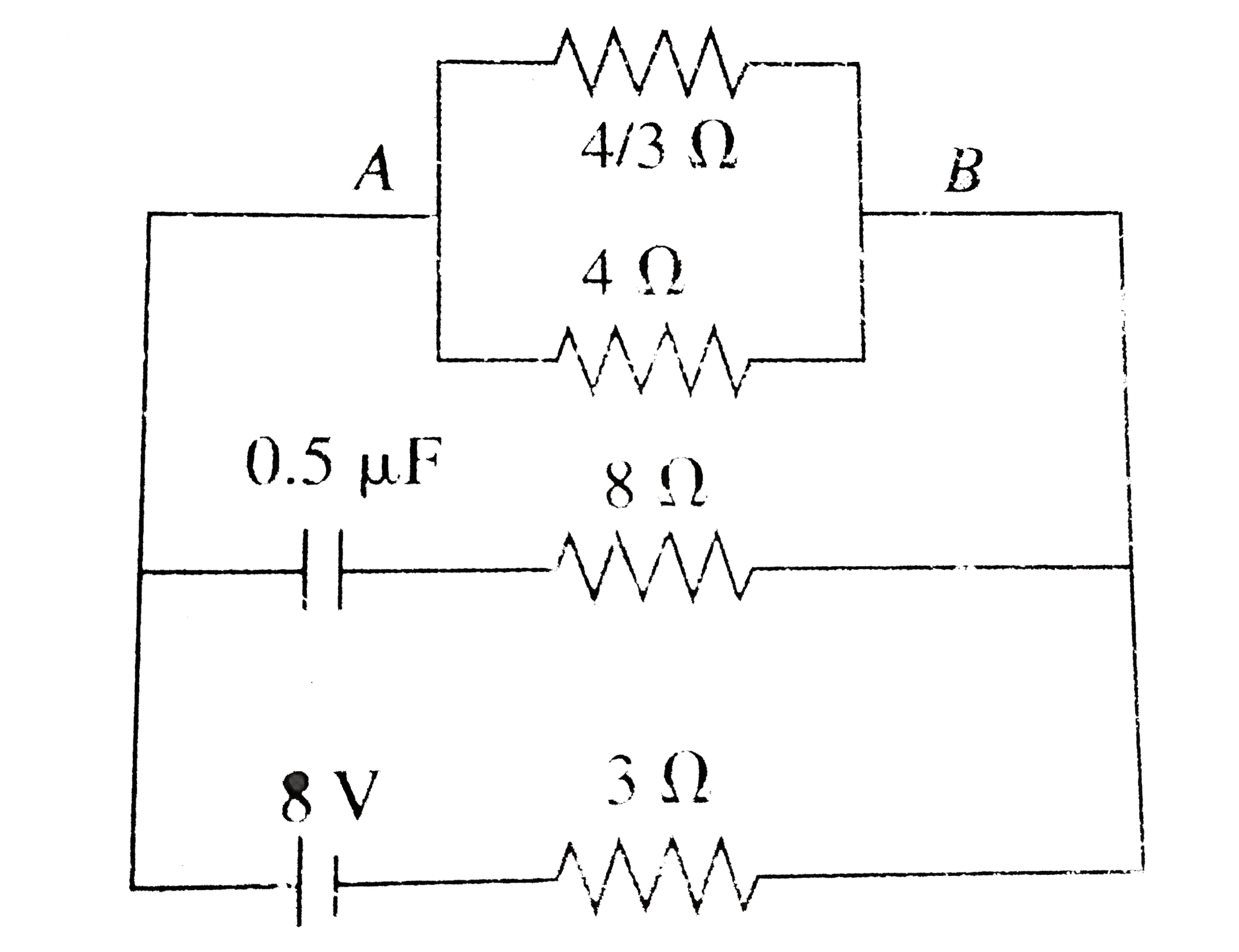 View Solution
View SolutionIn the circuit shown, current through the resistance2Ω isi1 and current through the resistance30Ω is i2. The ratio i1i2 is equal to
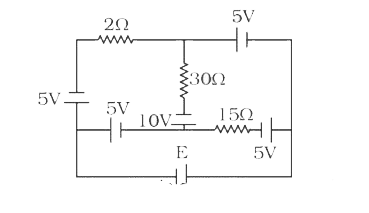 View Solution
View SolutionIn the circuit shown in Fig.6.2, the heat produced in 5Ω resistor, due to the current flowing through it is 10 calorie per second. Find the heat produced in 4Ω resistor.
View SolutionA coil of inductance L=2.0μH and resitance R=1.0Ω is connected to a source of constant emfE=3.0V. A resistance Rs=2.0Ω is connected in parallel with the coil. Find the amount of heat generated in the coil after the swich Sw is disconnecied. The internal resistance of the source is negligible.
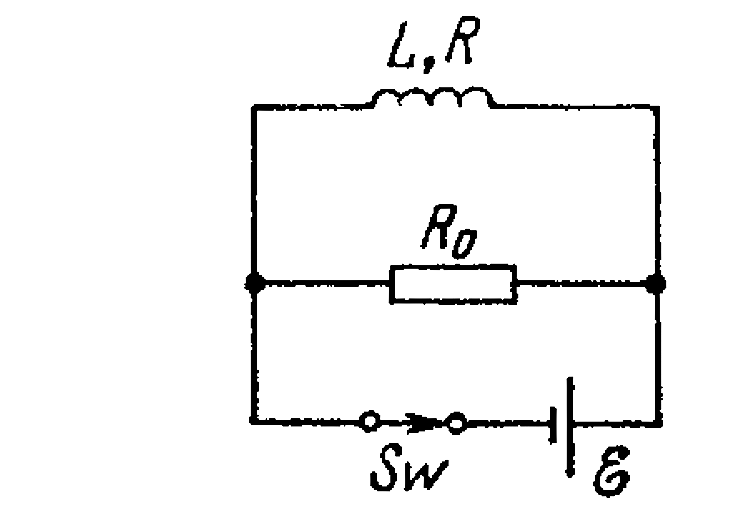 View Solution
View SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
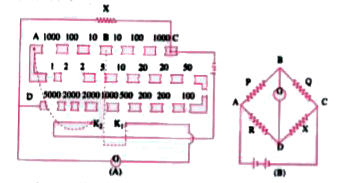
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method the necessary precaution to be taken is/areView SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
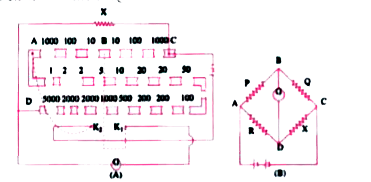
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method, height of the lower meniscus from free surface of water is 3cm while inner radius of capillary tubne is found to be 0.5cm. Then compute surface tension of water using this data. [Take contact angle between glass and water as 0° and g=9.8ms−2 ]View SolutionThe four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
AB=100Ω,BC=10Ω,CD=5Ω,andDA=60Ω.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.View Solution

