A variable capacitor is adjusted to its lowest capacitance and is connected with a source of constant voltage for a long time. The resistance of connecting wires is . At , its capacitance starts to increase so that a constant current starts to flow through the circuit. Calculate at time ,
(i) Power supplied by the source
(ii) thermal power generated in the connecting wire
(iii) rate of increase of electrostatic energy stored in capacitor
(iv) What do you infer from the above three results?
To solve the question, we will break it down into four parts as requested.
Given:
- Lowest capacitance of the capacitor: C0
- Constant voltage source: V
- Resistance of connecting wires: R
- Constant current flowing through the circuit: I
(i) Power Supplied by the Source
The power supplied by the source in an electrical circuit is given by the formula:
P=V⋅I
So, the power supplied by the source is:
P=V⋅I
(ii) Thermal Power Generated in the Connecting Wire
The thermal power generated in the connecting wire due to the resistance R can be calculated using Joule's law, which states:
Pthermal=I2⋅R
So, the thermal power generated in the connecting wire is:
Pthermal=I2⋅R
(iii) Rate of Increase of Electrostatic Energy Stored in the Capacitor
The electrostatic energy U stored in a capacitor is given by:
U=12CV2
When the capacitance increases, the charge Q on the capacitor can be expressed as:
Q=C0V+I⋅t
The potential difference across the capacitor when a current I flows is:
VC=V−I⋅R
The rate of change of electrostatic energy dUdt can be found as follows:
dUdt=12⋅dQdt⋅VC+12⋅Q⋅dVCdt
Since dQdt=I and VC=V−I⋅R, we have:
dUdt=12⋅I⋅(V−I⋅R)
Thus, the rate of increase of electrostatic energy stored in the capacitor is:
dUdt=12(V⋅I−I2⋅R)
(iv) Inference from the Above Three Results
From the results obtained, we can infer the following:
- The total power supplied by the source is used for two purposes: to generate thermal energy in the connecting wires and to increase the electrostatic energy stored in the capacitor.
- The difference between the power supplied by the source and the thermal power generated in the wires is the rate at which electrostatic energy is being stored in the capacitor.
- As the capacitance increases, it indicates that the plates of the capacitor are moving closer together, which leads to an increase in stored energy.
- Lowest capacitance of the capacitor: C0
- Constant voltage source: V
- Resistance of connecting wires: R
- Constant current flowing through the circuit: I
P=V⋅I
P=V⋅I
Pthermal=I2⋅R
Pthermal=I2⋅R
U=12CV2
Q=C0V+I⋅t
VC=V−I⋅R
dUdt=12⋅dQdt⋅VC+12⋅Q⋅dVCdt
dUdt=12⋅I⋅(V−I⋅R)
dUdt=12(V⋅I−I2⋅R)
- The total power supplied by the source is used for two purposes: to generate thermal energy in the connecting wires and to increase the electrostatic energy stored in the capacitor.
- The difference between the power supplied by the source and the thermal power generated in the wires is the rate at which electrostatic energy is being stored in the capacitor.
- As the capacitance increases, it indicates that the plates of the capacitor are moving closer together, which leads to an increase in stored energy.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.122videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective8videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
A resistance R1 is connected to a source of constant voltage . On connecting a resistance R2 in series with R1
View SolutionFind capacitive reactance of a capacitor connected to a dc source.
View SolutionA charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
View SolutionThe ratio of distance of two satellites from the centre of earth is 1 : 4. The ratio of their time periods of rotation will be :
View SolutionA capacitor of capacitance 10μF is connected to an AC source and an AC Ammeter. If the source voltage varies as V=50√2sin100t, the reading of the ammeter is
View SolutionA capacitor of capacitance 5μF is connected to a source of constant emf of 200V,Then switch was shifted to contact 2 from contact 1. Find the amount of heat generated in the 400Ω resistance.
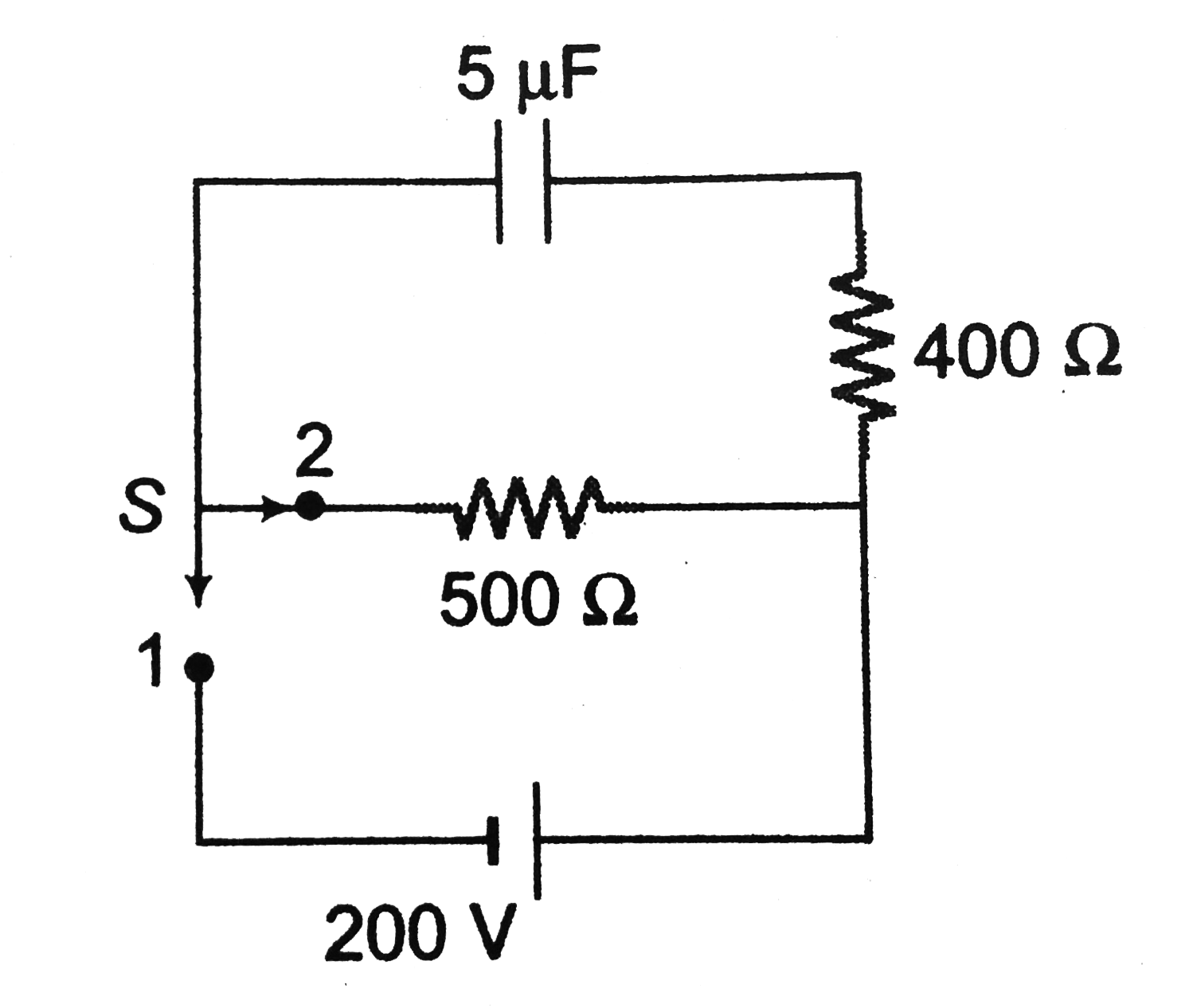 View Solution
View SolutionAn uncharged capacitor of capacitance C is connected with a battery of EMF V and a resistance R. The switch is closed at t=0. The time instant at which the current in the circuit is V4R is t=
View SolutionTime constant of the given circuit is τ If the battery is replaced by an ac source having voltage V=V0cosωt , power factor or the circuit will be
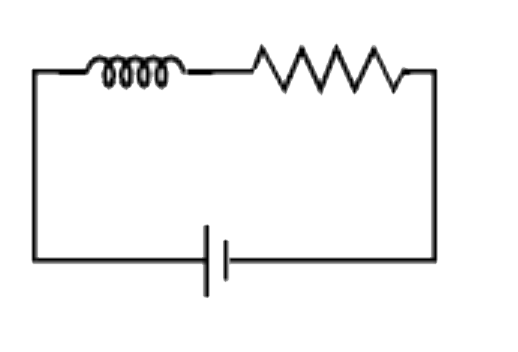 View Solution
View SolutionA circuit containing an inductance and a resistance connected in series, has an AC source of 200V, 50Hz connected across it. An AC current of 10A rms flows through th ecircuit and the power loss is measured to be 1W.
View SolutionA capacitor is connected to a variable source of potential. Current flowing in the circuit and potential across the plates of capacitor at time t are shown in figure.

Capacity of the capacitor isView Solution

