Question

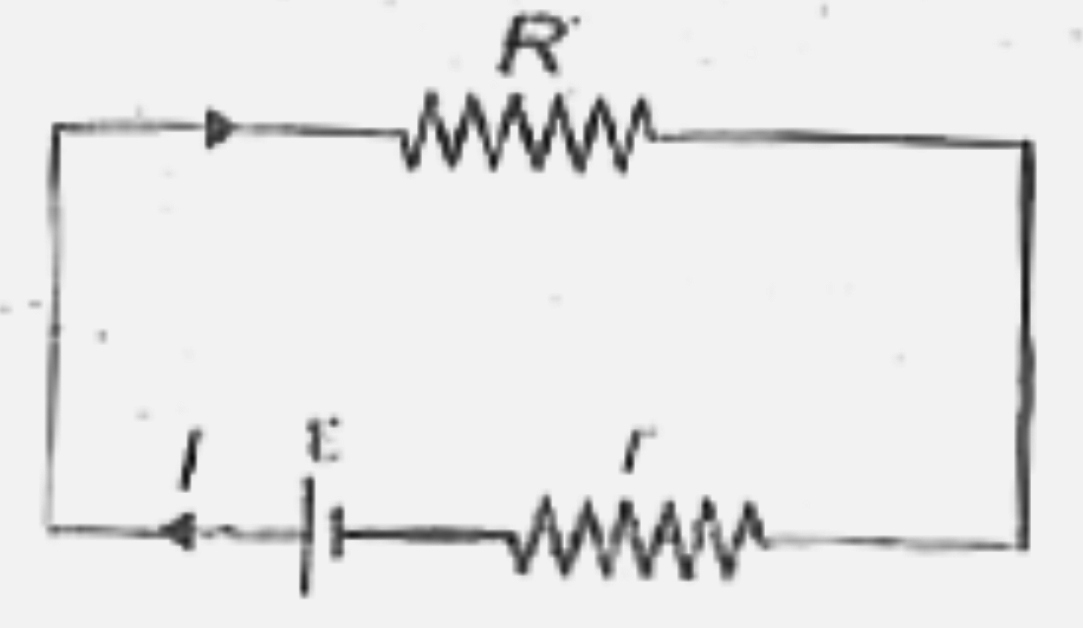
A cell of internal resistances $r$ is connected to a load of resistance $R$ . Energy is dissipated in the load, but some thermal energy is also wasted in the cell. The efficiency of such an arrangement is found from the expression
( Energy dissipated in the load )/( Energy dissipated in the complete circuit)
Which of the following gives the efficiency in this case?

Options

A. `( r ) /( R )`
B. `( R )/( r)`
C. `( r )/( R + r)`
D. `( R ) /( R + r )`

Answer

D

Explanation

To solve the problem, we need to determine the efficiency of a circuit consisting of a cell with internal resistance $$r$$ connected to a load with resistance $$R$$. The efficiency is given by the ratio of the energy dissipated in the load to the total energy dissipated in the entire circuit.

1. Understanding the Circuit:
- We have a cell with an electromotive force (emf) \( E \) and an internal resistance \( r \).
- The load resistance is \( R \).
- The total resistance in the circuit is \( R + r \).

2. Calculating the Current:
- The current \( I \) flowing through the circuit can be calculated using Ohm's law:
\( I = \frac{E}{R + r} \)

3. Energy Dissipated in the Load:
- The energy dissipated in the load \( H_R \) can be calculated using the formula for power (which is energy per unit time) and the relationship \( P = I^2 R \):
\( H_R = I^2 R \)
- Substituting the expression for \( I \):
\( H_R = \left(\frac{E}{R + r}\right)^2 R = \frac{E^2 R}{(R + r)^2} \)

4. Calculating Total Energy Dissipated in the Circuit:
- The total energy dissipated \( H_T \) in the circuit includes the energy dissipated in both the load and the internal resistance:
\( H_T = H_R + H_r \)
- The energy dissipated in the internal resistance \( H_r \) is given by:
\( H_r = I^2 r = \left(\frac{E}{R + r}\right)^2 r = \frac{E^2 r}{(R + r)^2} \)
- Therefore, the total energy dissipated in the circuit is:
\( H_T = H_R + H_r = \frac{E^2 R}{(R + r)^2} + \frac{E^2 r}{(R + r)^2} = \frac{E^2 (R + r)}{(R + r)^2} \)

5. Calculating Efficiency:
- The efficiency \( \eta \) is defined as the ratio of the energy dissipated in the load to the total energy dissipated in the circuit:
\( \eta = \frac{H_R}{H_T} \)
- Substituting the expressions for \( H_R \) and \( H_T \):
\( \eta = \frac{\frac{E^2 R}{(R + r)^2}}{\frac{E^2 (R + r)}{(R + r)^2}} = \frac{R}{R + r} \)

6. Final Result:
- Thus, the efficiency of the arrangement is given by:
\( \eta = \frac{R}{R + r} \)

Conclusion:
The efficiency of the circuit arrangement is \( \frac{R}{R + r} \).