The heat generated through 4Ωand9Ω resistances separately , when a capacitor pf 100myF capacity charged to 200V is discharged one by one , will be
2 J and 8 J, respectively
8 J and 2 J, respectively
2 J and 4 J, respectively
2 J and 2 J, respectively
The correct Answer is:D
To solve the problem of calculating the heat generated through 4 ohm and 9 ohm resistances when a capacitor of 100 µF capacity charged to 200 V is discharged, we can follow these steps:
Step 1: Understand the Energy Stored in the Capacitor
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- C is the capacitance in farads (F),
- V is the voltage in volts (V).
Step 2: Substitute the Given Values
In this case:
- C=100μF=100×10−6F
- V=200V
Substituting these values into the formula:
U=12×(100×10−6)×(200)2
Step 3: Calculate the Energy
Now, we calculate U:
U=12×100×10−6×40000
U=12×100×10−6×4×104
U=12×100×4×10−2
U=200×10−2=2J
Step 4: Heat Generated in the Resistors
The energy stored in the capacitor is completely converted into heat when it discharges through the resistors. Therefore, the heat generated through both resistances (4 ohm and 9 ohm) will be equal to the energy stored in the capacitor.
Conclusion
Thus, the heat generated through both the 4 ohm and 9 ohm resistors when the capacitor is discharged will be:
- Heat through 4 ohm resistor: 2J
- Heat through 9 ohm resistor: 2J
Final Answer: The heat generated through both resistances is 2J and 2J respectively.
---
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- C is the capacitance in farads (F),
- V is the voltage in volts (V).
In this case:
- C=100μF=100×10−6F
- V=200V
U=12×(100×10−6)×(200)2
Now, we calculate U:
U=12×100×10−6×40000
U=12×100×10−6×4×104
U=12×100×4×10−2
U=200×10−2=2J
The energy stored in the capacitor is completely converted into heat when it discharges through the resistors. Therefore, the heat generated through both resistances (4 ohm and 9 ohm) will be equal to the energy stored in the capacitor.
Thus, the heat generated through both the 4 ohm and 9 ohm resistors when the capacitor is discharged will be:
- Heat through 4 ohm resistor: 2J
- Heat through 9 ohm resistor: 2J
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct5videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning6videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective8videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
A capacitor of capacitance 100(μ)F is connected across a battery of emf6.0V through a resistance of 20k(Ω)for 4.0s after the battery is disconnecting?
View SolutionA capacitor of capacitance 3μF is first charged by connecting it across a 10 V battery by closing key K1. Then it is allowed to get discharged through 2Ω and 4Ω resistors by closing the key K2. The total energy dissipated in the 4Ω resistor is equal to
 View Solution
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
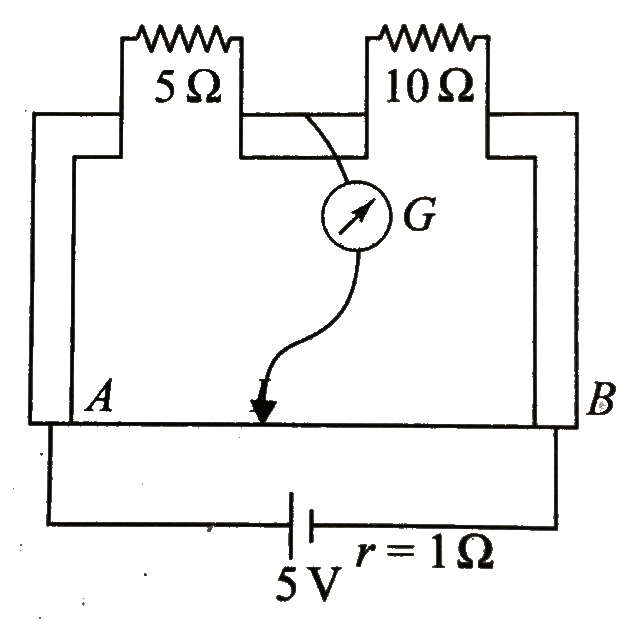 View Solution
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionA 8 μ F capacitor is charged by a 400 V supply through 0.1 M Ω resistance. The time taken by the capacitor to develop a potential difference of 300V is : (Given log104=0.602)
View SolutionA capacitor discharges through a resistance. The stored energy U0 in one capacitive time constant falls to
View SolutionA coil has resistance 30Ω and inductive reactance 20Ω at 50 Hz frequency. If an ac source of 200V, 100 Hz is connected across the coil, the current in the coil will be
View SolutionA battery has an open circuit potential difference 10 V between the terminals. When loads 9Ωand4Ω are connected one by one across the battery , the power in the load resistance is the same. The amount of heat approximately generated in one second in the load when a load of 5Ω Is connected across the battery will be
View SolutionA 100Ω resistance and a capacitor of 100Ω reactance are connected in series across a 220 V source. When the capacitor is 50% charged, the peak value of the displacement current is
View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View Solution

