Refer to Fig. .
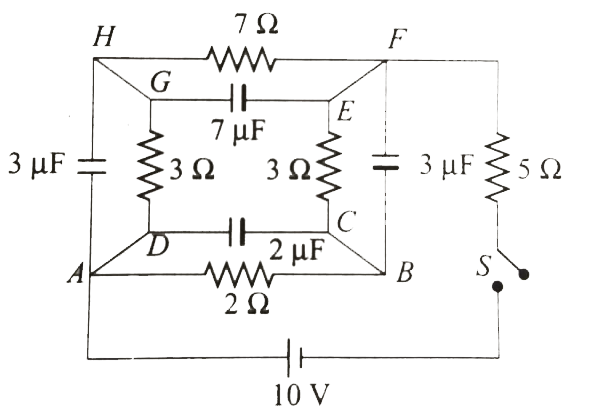
Long time after closing the switch , find the current through the resistor.
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
Initially, When all the capacitors are uncharged, they will act as conducting wires. Hence, all the resistances will be short - circuited. So no resistance occurs between . Thus current through the resistor will be .
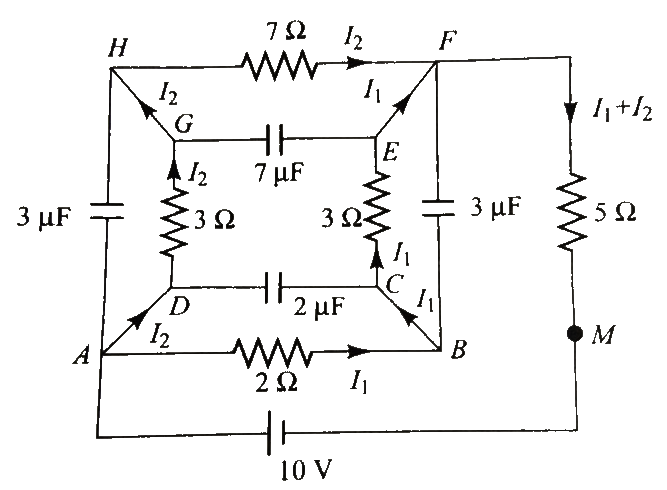
In steady state, distibution of current is shown.
Loop
or .....(I)
Loop
or .......(ii)
From Eqs. (i) and (ii) ,
Hence , current through the is . Potential
difference across the capacitor is
Energy in it is given by
Potential difference across is capacitor is
Energy in it is given by
Potential difference across the capacitor is
Energy in it is given by
potential difference across the capacitor is
Energy in it is given by
Thus , whole of the energy stored in all capacitors will be dissipated after the switch is opened. So the energy dissipated is .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Integer5videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Calculating Thermal Power in Resistance14videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning6videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
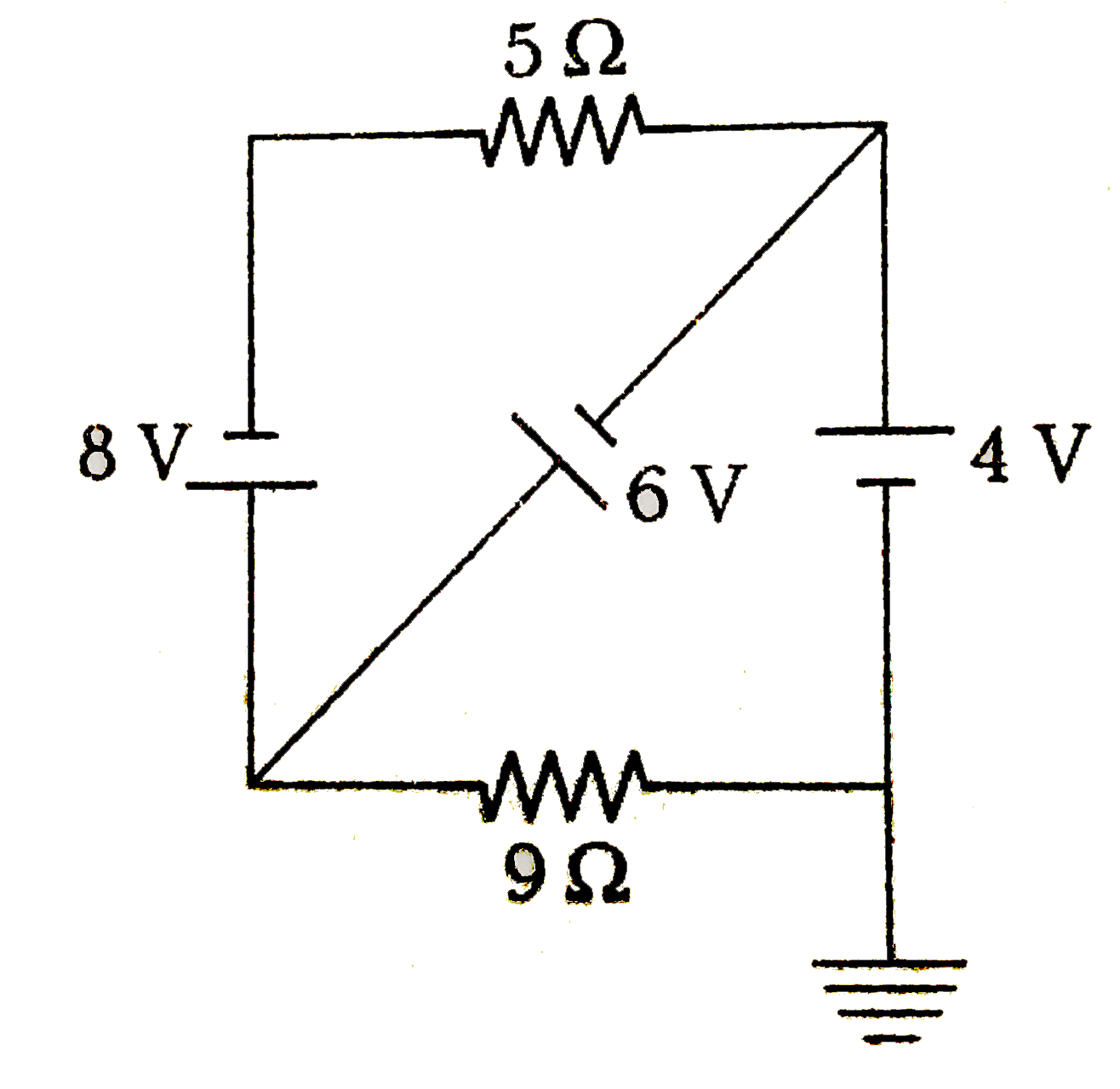
The current through the 5Ω resistor is
 View Solution
View SolutionCurrent through the 5Ω resistor is
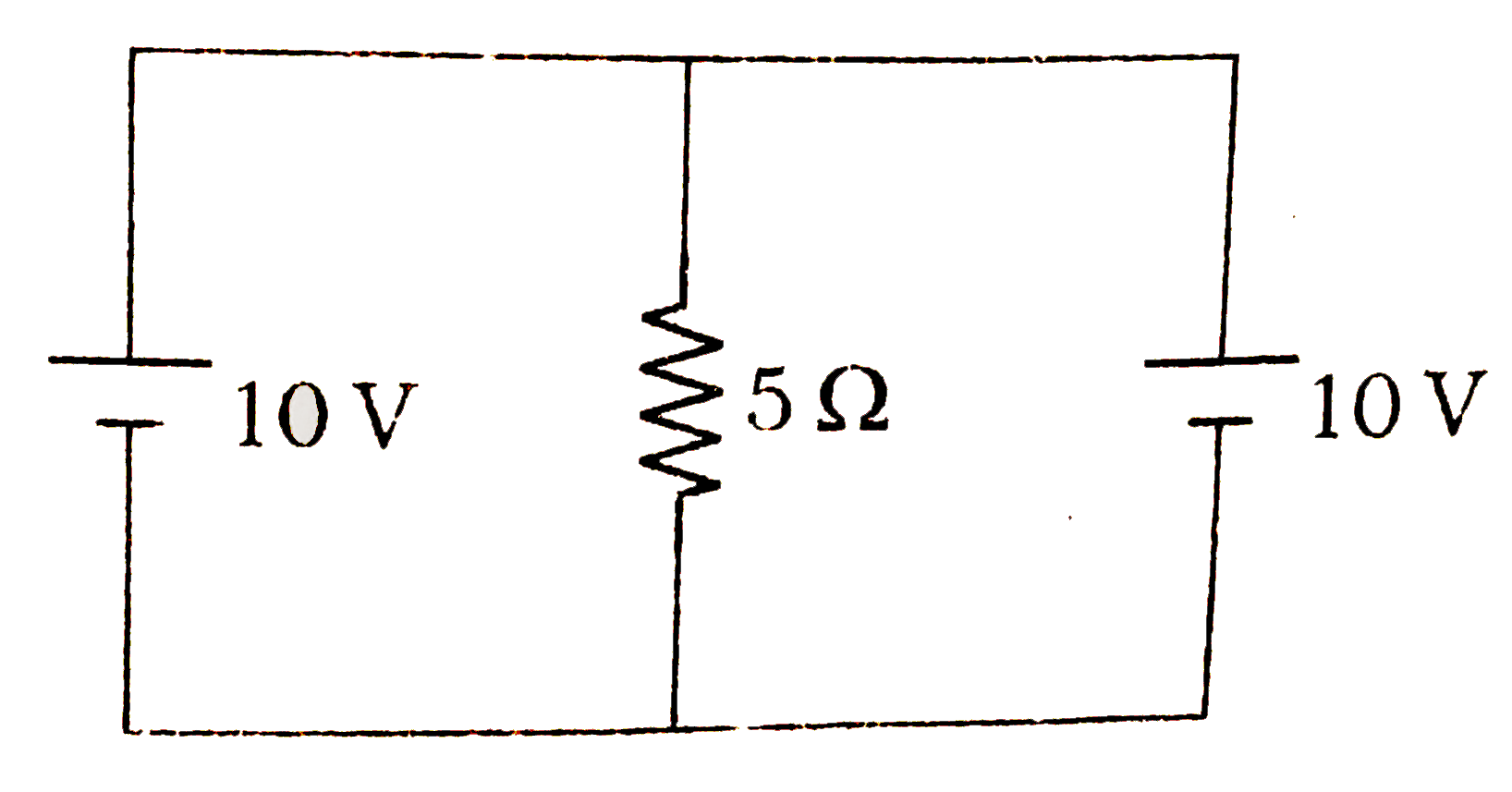 View Solution
View SolutionFind the current through 12Ω resistor in
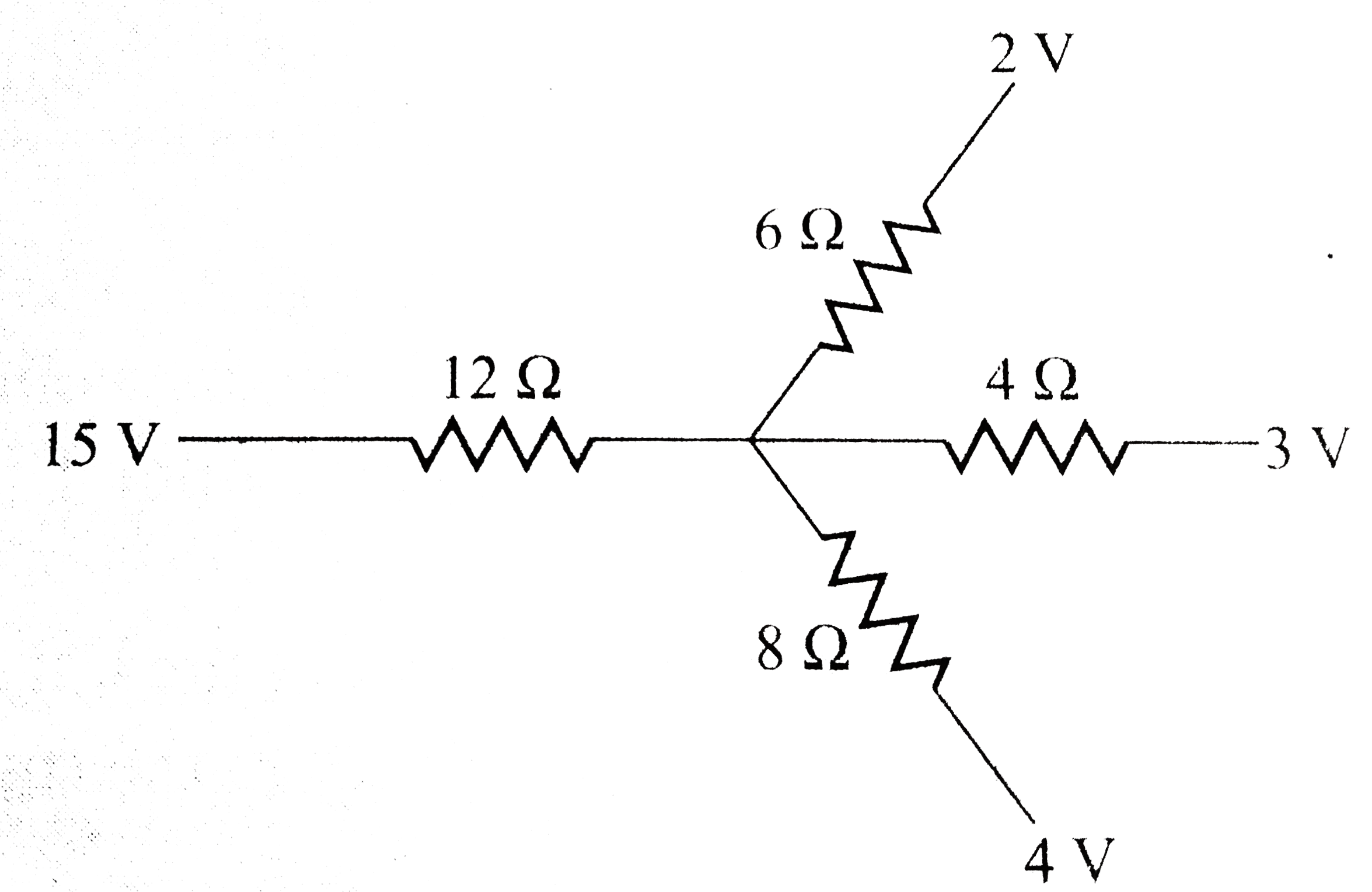 View Solution
View SolutionRefer to Fig. 7.49.
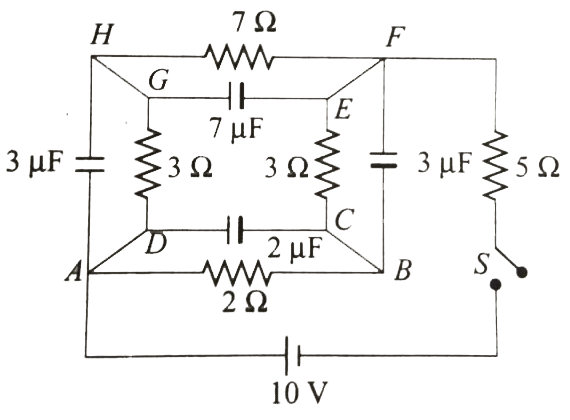
At t=0 , the switch is closed . Just after closing the switch, find the current through the 5Ω resistor.View SolutionFind the current through the 10(Ω)resistor shown in figure.
 View Solution
View SolutionFind the current through the 10(Ω)resistor shown in figure.
 View Solution
View SolutionThe value of current through 2Ω resistor is
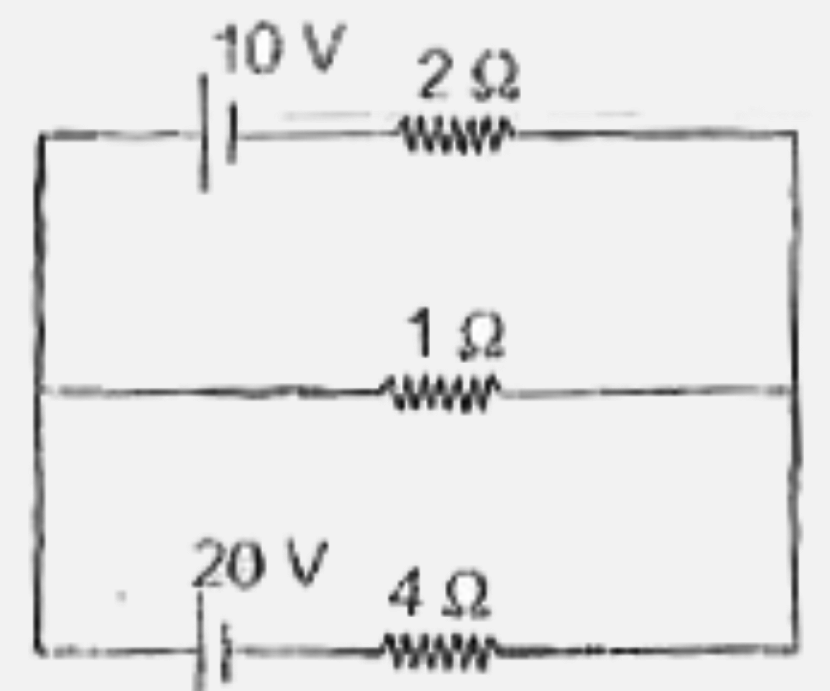 View Solution
View SolutionWhen the switch is closed, the initial current through the 1Ω resistor is
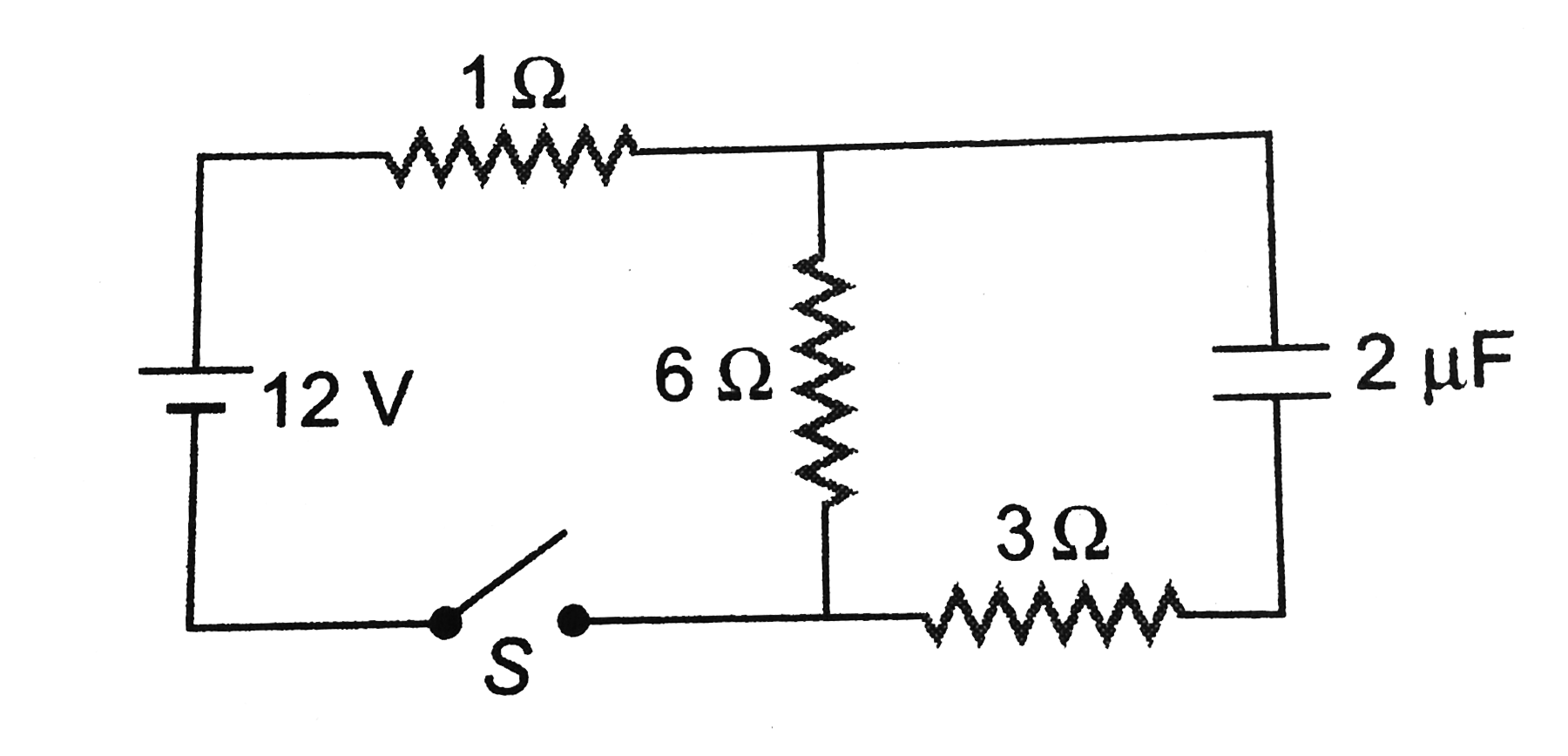 View Solution
View SolutionIn the circuit diagram shown in find the current through the 1Ω resistor.
 View Solution
View SolutionElectric current through 400Ω resistor is :
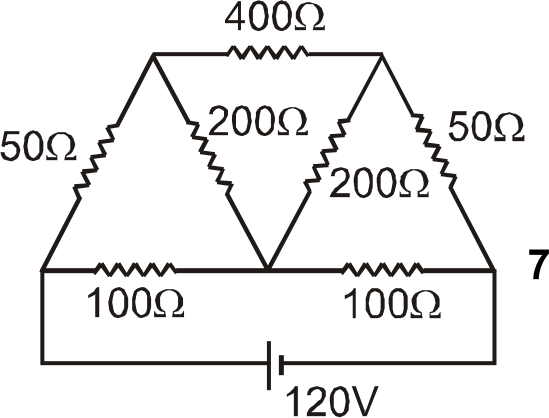 View Solution
View Solution

