Given are four arrangements of three fixed electric charges. In each arrangement, a point labeled P is also identified. A test charge +q is placed at P. All of the charges are of the same magnitude Q, but they can be either positive or negative as indicated. The charged and point P all lie on a straight line. the distances between adjacent items, either between two charges or between a charge and point P, are all the same.
I. ⊕,⊕,⊕,⋅P, II. ⊕,⊕,P⋅,−
III. ⊕,⊕,−,P⋅, IV. ⊕,−,⊕,P⋅.
Correct order of choices in a decreasing order of magnitude of force on P is
II>I>III>IV
I>II>III>IV
II>I>IV>III
III>IV>I>II
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the test charge +q at point P for each of the four arrangements of charges. We will calculate the net force on the test charge for each arrangement and then compare them.
Step 1: Analyze Arrangement I
Arrangement I: +Q,+Q,+Q,P
- The forces acting on +q at point P due to the three +Q charges are all repulsive.
- The distances from P to each charge are equal, say r.
- The force due to each charge is given by Coulomb's law:
F=kQqr2
- Since all three forces are repulsive and equal, the total force F1 on P is:
F1=3⋅kQqr2
Step 2: Analyze Arrangement II
Arrangement II: +Q,+Q,P,−Q
- The force from the first +Q charge on P is attractive:
F1=kQqr2
- The force from the second +Q charge on P is also attractive:
F2=kQqr2
- The force from the −Q charge on P is repulsive:
F3=kQqr2
- The net force F2 on P is:
F2=F1+F2−F3=kQqr2+kQqr2−kQqr2=kQqr2
Step 3: Analyze Arrangement III
Arrangement III: +Q,+Q,−Q,P
- The force from the first +Q charge on P is attractive:
F1=kQqr2
- The force from the second +Q charge on P is also attractive:
F2=kQqr2
- The force from the −Q charge on P is repulsive:
F3=kQq(2r)2=kQq4r2
- The net force F3 on P is:
F3=F1+F2−F3=kQqr2+kQqr2−kQq4r2=4kQq4r2−kQq4r2=3kQq4r2
Step 4: Analyze Arrangement IV
Arrangement IV: +Q,−Q,+Q,P
- The force from the first +Q charge on P is repulsive:
F1=kQqr2
- The force from the −Q charge on P is attractive:
F2=kQqr2
- The force from the last +Q charge on P is also repulsive:
F3=kQq(2r)2=kQq4r2
- The net force F4 on P is:
F4=F1−F2+F3=kQqr2−kQqr2+kQq4r2=kQq4r2
Step 5: Compare the Forces
Now we have the following forces for each arrangement:
1. F1=3kQqr2
2. F2=kQqr2
3. F3=3kQq4r2
4. F4=kQq4r2
Step 6: Order the Forces
Now we can order the forces in decreasing magnitude:
- F1>F3>F2>F4
Conclusion
The correct order of choices in decreasing order of magnitude of force on P is:
1. Arrangement I
2. Arrangement III
3. Arrangement II
4. Arrangement IV
Arrangement I: +Q,+Q,+Q,P
- The distances from P to each charge are equal, say r.
- The force due to each charge is given by Coulomb's law:
F=kQqr2
- Since all three forces are repulsive and equal, the total force F1 on P is:
F1=3⋅kQqr2
Arrangement II: +Q,+Q,P,−Q
F1=kQqr2
- The force from the second +Q charge on P is also attractive:
F2=kQqr2
- The force from the −Q charge on P is repulsive:
F3=kQqr2
- The net force F2 on P is:
F2=F1+F2−F3=kQqr2+kQqr2−kQqr2=kQqr2
Arrangement III: +Q,+Q,−Q,P
F1=kQqr2
- The force from the second +Q charge on P is also attractive:
F2=kQqr2
- The force from the −Q charge on P is repulsive:
F3=kQq(2r)2=kQq4r2
- The net force F3 on P is:
F3=F1+F2−F3=kQqr2+kQqr2−kQq4r2=4kQq4r2−kQq4r2=3kQq4r2
Arrangement IV: +Q,−Q,+Q,P
F1=kQqr2
- The force from the −Q charge on P is attractive:
F2=kQqr2
- The force from the last +Q charge on P is also repulsive:
F3=kQq(2r)2=kQq4r2
- The net force F4 on P is:
F4=F1−F2+F3=kQqr2−kQqr2+kQq4r2=kQq4r2
Now we have the following forces for each arrangement:
1. F1=3kQqr2
2. F2=kQqr2
3. F3=3kQq4r2
4. F4=kQq4r2
Now we can order the forces in decreasing magnitude:
- F1>F3>F2>F4
The correct order of choices in decreasing order of magnitude of force on P is:
1. Arrangement I
2. Arrangement III
3. Arrangement II
4. Arrangement IV
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
Two free point charges +qand+4q are placed apart a distance x. A third charge is so placed that all the three charges are in equilibrium. Then
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionTwo charge +q and −q are placed at distance r. Match the following two columns when distance between them is charged to r'.
 View Solution
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionTwo positive point charges of unequal magnitude are placed at a certain distance apart. A small positive test charge is placed at null point, then
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is
 View Solution
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
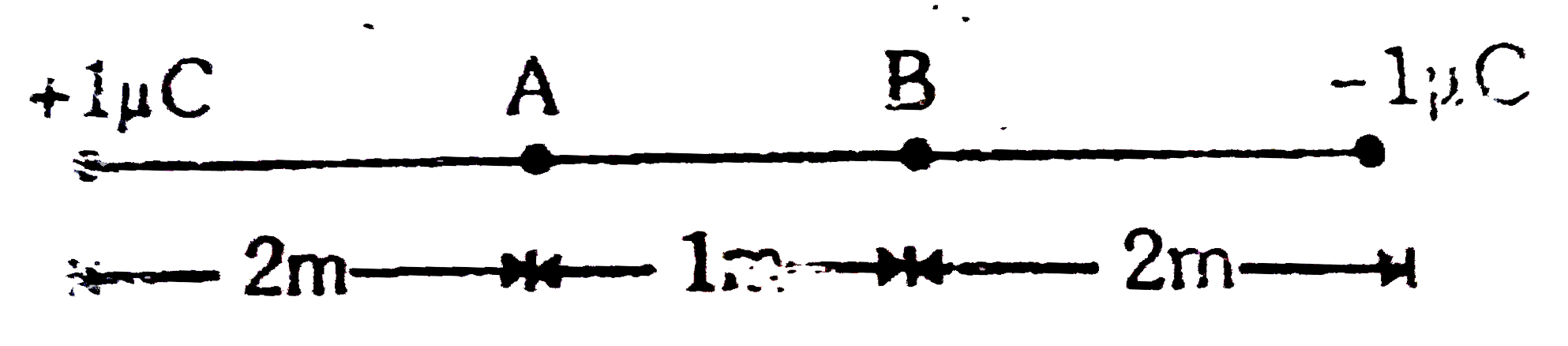 View Solution
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View Solution

