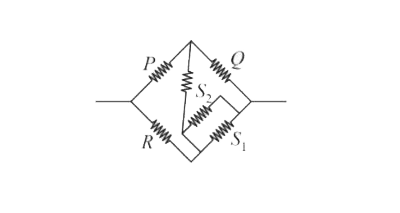
In a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
PQ=R(S1+S2)2S1S2
PQ=(RS1+S2)
PQ=2RS1+S2
PQ=R(S1+S2)S1S2
The correct Answer is:D
To solve the problem regarding the condition for a Wheatstone bridge to be balanced with resistances P, Q, R, S1, and S2, we can follow these steps:
1. Understand the Configuration: In a Wheatstone bridge, we have four resistances. Three of them are P, Q, and R, and the fourth arm consists of two resistances S1 and S2 connected in parallel.
2. Identify the Condition for Balance: The Wheatstone bridge is balanced when there is no current flowing through the galvanometer (or the branch connecting the two midpoints of the bridge). This occurs when the ratio of the resistances in one branch is equal to the ratio of the resistances in the other branch.
3. Set Up the Ratios: For the bridge to be balanced, we can express the condition as:
PQ=RSequivalent
where Sequivalent is the equivalent resistance of S1 and S2 in parallel.
4. Calculate the Equivalent Resistance: The equivalent resistance Sequivalent for two resistances S1 and S2 connected in parallel is given by the formula:
Sequivalent=S1S2S1+S2
5. Substitute the Equivalent Resistance: Substitute Sequivalent back into the balance condition:
PQ=RS1S2S1+S2
6. Cross-Multiply to Simplify: Cross-multiplying gives:
P⋅S1S2S1+S2=Q⋅R
7. Rearranging the Equation: Rearranging the equation leads to:
P⋅S1S2=Q⋅R⋅(S1+S2)
8. Final Form of the Condition: This can be expressed as:
PQ=R⋅S1+S2S1S2
Conclusion:
The condition for the Wheatstone bridge to be balanced is:
PQ=R⋅S1+S2S1S2
PQ=RSequivalent
where Sequivalent is the equivalent resistance of S1 and S2 in parallel.
Sequivalent=S1S2S1+S2
PQ=RS1S2S1+S2
P⋅S1S2S1+S2=Q⋅R
P⋅S1S2=Q⋅R⋅(S1+S2)
PQ=R⋅S1+S2S1S2
The condition for the Wheatstone bridge to be balanced is:
PQ=R⋅S1+S2S1S2
Similar Questions
In a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)
 View Solution
View SolutionIn a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)
 View Solution
View SolutionResistance R,2R,4R,8R ...... ∞ are connected in parallel. What is their resutlant resistance will be
View SolutionThe wire of same dimension but resistivities(p1) and (p2)are connected in parallel. The equivalent resistivity of the combination is
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionIn a balanced wheatstone's network, the resistances in the arms Q and S are interchanged. As result of this:
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
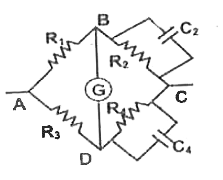
View SolutionConsider a Wheatstone bridge with resistance and capacitance connected as shown Find the condition on the resistance and the capacitance such that the bridge remains balanced at all times.
 View Solution
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View Solution

