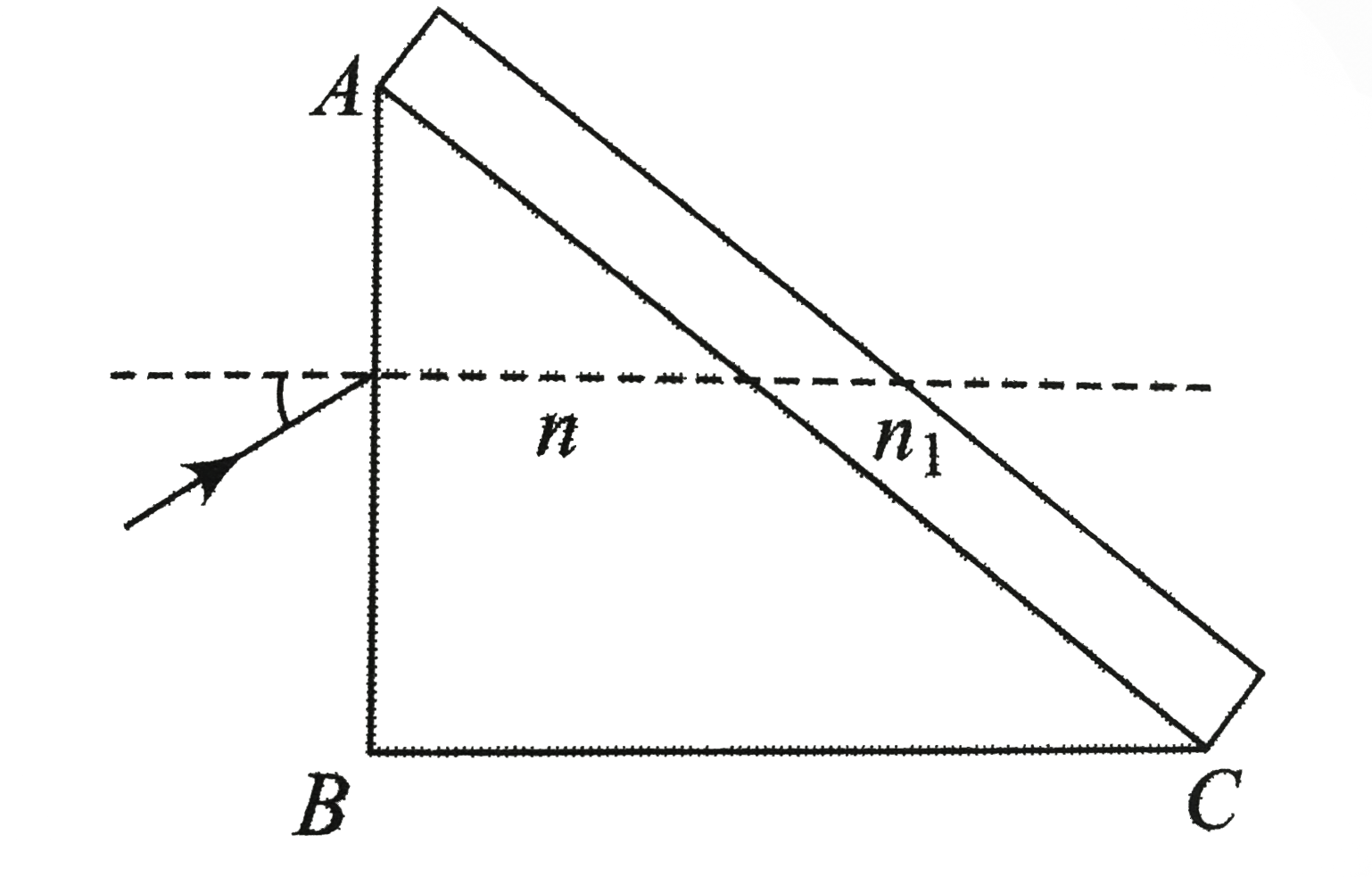
A right angles prism $(45^{\circ}, 90^{\circ}, 45^{\circ})$ of refractive index n has a plate of refractive index $(n_{1} < n)$ cemented to its diagonal face. The assembley is in air. A ray is incident on AB.
a. Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle.
b. Assuming $n = 1.351$ , calculate the angle of incidence at AB for which the refracted rey passes through the diagonal face undeviated.
$A right angles prism (45^(@),90^(@), 45^(@)) of refractive index n has a plate of refractive index (n(1)ltn) cemented to its diagonal face. The assembley is in air. A ray is incident on AB. a. Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle. b. Assuming n=1.351, calculate the angle of incidence at AB for which the refracted rey passes through the diagonal face undeviated.$

Video Solution

Text Solution

Verified by Experts

a. $sin C = \frac{n_{1}}{n}$
From Figure , $(90^{\circ} - r_{1}) + 45^{\circ} + (90^{\circ} - C) = 180^{\circ}$
$\Rightarrow r_{1} = 45^{\circ} - C$
From Snell's law,
$\frac{sin i}{{sin r}_{1}} = n$
$∴ sin i = n {sin r}_{1}$
$= n sin (45^{\circ} - C)$
$= n ({sin 45}^{\circ} cos C - {cos 45}^{\circ} sin C)$
$= \frac{n}{\sqrt{2}} (cos C - sin C)$
$\frac{n}{\sqrt{2}} [\sqrt{1 - {sin}^{2} C} - sin C]$
$[\sqrt{1 - {(\frac{n_{1}}{n})}^{2}} - \frac{n_{1}}{n}]$
$\frac{1}{\sqrt{2}} [\sqrt{(n^{2} - n_{1}^{2})} - n_{1}]$
$\Rightarrow i = {sin}^{- 1} {\frac{1}{\sqrt{2}} (\sqrt{n^{2} - n_{1}^{2}}) - n_{1}}$
b. When refracted ray passes through the diagonal face undeflected, the incidence at diagonal face is perpendicular.
$r_{2} = 0$ so $r_{1} + r_{2} = 45^{\circ} \Rightarrow r_{1} = 45^{\circ}$
Again, $\frac{sin i}{{sin r}_{1}} = n \Rightarrow sin i = n {sin r}_{1} = 1.352 {sin 45}^{\circ}$
or $sin i = 1.3520020 \frac{1}{\sqrt{2}} = 0.956$
or $i = {sin}^{- 1} (0.956) = 72^{\circ} 58^{'}$ .

Updated on:21/07/2023

A ray of light passes through an equilateral prism (refractive index $1.5$ ) such that angle of incidence is equal to angle of emergence and the latter is equal to $3 / 4 t h$ of the angle of prism. Calculate the angle of deviation.
A $60^{\circ}$
B $30^{\circ}$
C $45^{\circ}$
D $120^{\circ}$