A horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
To solve the problem of finding the net deviation of a beam of light passing through a solid glass sphere, we can follow these steps:
Step 1: Understand the Geometry of the Problem
We have a solid glass sphere with radius R and refractive index μ. A horizontal ray of light is incident on the sphere. We need to analyze how this ray behaves as it enters and exits the sphere.
Hint: Visualize the ray's path as it enters and exits the sphere. Draw a diagram if necessary.
Step 2: Identify the Angles of Incidence and Refraction
Let the angle of incidence at the first surface of the sphere be I. According to Snell's law, we can relate the angle of incidence I to the angle of refraction R using the formula:
sinI=μsinR
Hint: Remember that Snell's law applies at the boundary between two media with different refractive indices.
Step 3: Express the Angle of Refraction
From Snell's law, we can express the angle of refraction R as:
R=sin−1(sinIμ)
Hint: This equation helps us find the angle at which the ray travels inside the sphere.
Step 4: Calculate the Deviation at Each Surface
When the ray enters the sphere, it deviates by an angle D1 given by:
D1=I−R
When the ray exits the sphere, it will again deviate by the same amount D2 (since it exits into the same medium, air):
D2=I−R
Hint: The total deviation when the ray exits is the sum of the deviations at both surfaces.
Step 5: Calculate the Total Deviation
The total deviation D of the ray as it passes through the sphere is:
D=D1+D2=(I−R)+(I−R)=2(I−R)
Hint: This step combines the deviations from both the entry and exit points.
Step 6: Substitute for R
Now, substitute the expression for R into the total deviation formula:
D=2(I−sin−1(sinIμ))
Hint: This final expression gives you the net deviation of the beam as it emerges from the sphere.
Final Answer
Thus, the net deviation of the beam when it emerges from the other side of the sphere is:
D=2(I−sin−1(sinIμ))
We have a solid glass sphere with radius R and refractive index μ. A horizontal ray of light is incident on the sphere. We need to analyze how this ray behaves as it enters and exits the sphere.
Let the angle of incidence at the first surface of the sphere be I. According to Snell's law, we can relate the angle of incidence I to the angle of refraction R using the formula:
sinI=μsinR
From Snell's law, we can express the angle of refraction R as:
R=sin−1(sinIμ)
When the ray enters the sphere, it deviates by an angle D1 given by:
D1=I−R
When the ray exits the sphere, it will again deviate by the same amount D2 (since it exits into the same medium, air):
D2=I−R
The total deviation D of the ray as it passes through the sphere is:
D=D1+D2=(I−R)+(I−R)=2(I−R)
Now, substitute the expression for R into the total deviation formula:
D=2(I−sin−1(sinIμ))
Thus, the net deviation of the beam when it emerges from the other side of the sphere is:
D=2(I−sin−1(sinIμ))
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.4
12 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
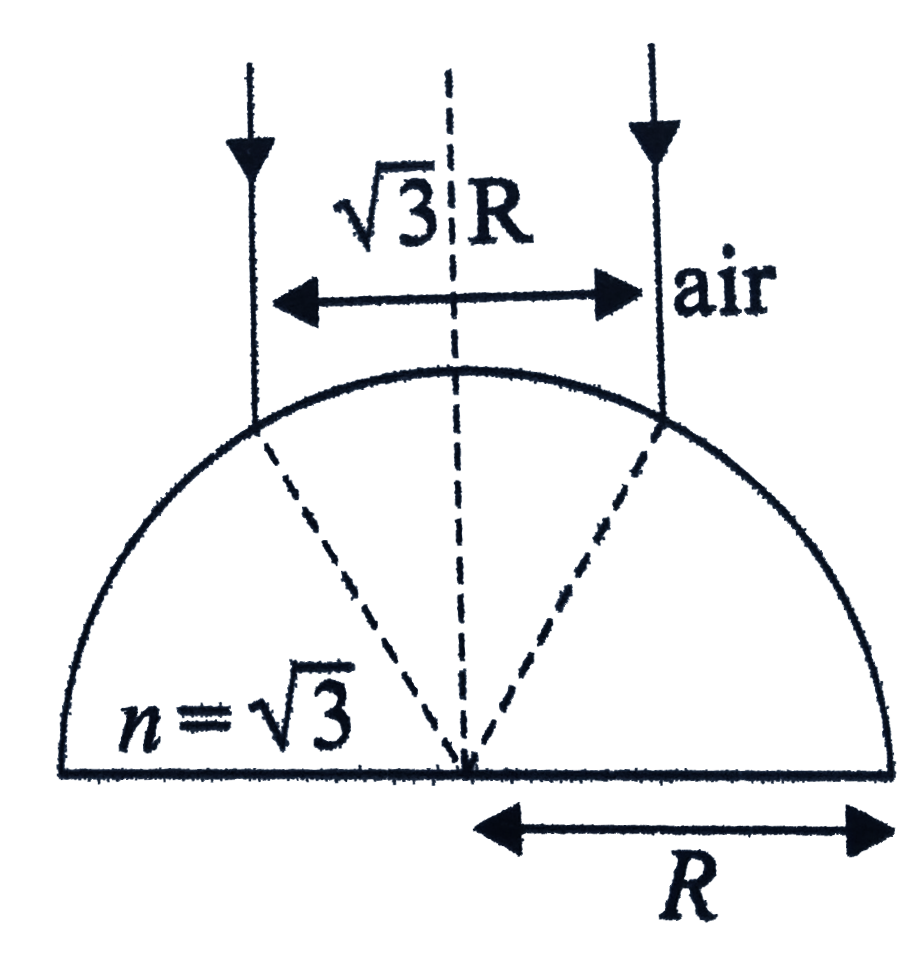
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemisphere of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemisphere.

View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index if the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
View SolutionA ray of light is incident on the surface of a sphere of refractive index √72 other half of sphere is silvered. After refraction it is reflected and then refracted out of sphere again such that the total deviation is minimum then total deviation of the ray will be (sin410−√37)

View SolutionOne side of a glass slab is silvered as shown. A ray of light is incident on the other side at angle of incidence i=45∘ . Refractive index of glass is given as 1.5. The deviation of the ray of light from its initial path when it comes out of the slab is

View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractive index n if the beam finally gets focused at a point situated at a distance=2×(radius of sphere) form the center of the sphere then find n?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution
