A narrow parallel beam of light is incident on a transparent sphere of refractive index n if the beam finally gets focused at a point situated at a distance=2×(radius of sphere) form the center of the sphere then find n?
43
32
−46
−23
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a transparent sphere with a refractive index n and a parallel beam of light incident on it. The light beam focuses at a distance of 2R from the center of the sphere, where R is the radius of the sphere.
Step 2: Use the lens maker's formula
The lens maker's formula for a spherical surface is given by:
n2v−n1u=n2−n1R
Here, n1=1 (the refractive index of air), n2=n (the refractive index of the sphere), v is the image distance, u is the object distance, and R is the radius of curvature.
Step 3: Assign values to variables
- The image distance v is given as 2R.
- The object distance u is initially considered to be at infinity since the beam is parallel.
Step 4: Substitute values into the lens maker's formula
Substituting n1, n2, and v into the lens maker's formula:
n2R−1∞=n−1R
Since 1∞=0, the equation simplifies to:
n2R=n−1R
Step 5: Cross-multiply to solve for n
Cross-multiplying gives:
n=2(n−1)
Expanding this:
n=2n−2
Step 6: Rearranging the equation
Rearranging gives:
2=2n−n
2=n
Step 7: Conclusion
Thus, the refractive index n is:
n=43
We have a transparent sphere with a refractive index n and a parallel beam of light incident on it. The light beam focuses at a distance of 2R from the center of the sphere, where R is the radius of the sphere.
The lens maker's formula for a spherical surface is given by:
n2v−n1u=n2−n1R
Here, n1=1 (the refractive index of air), n2=n (the refractive index of the sphere), v is the image distance, u is the object distance, and R is the radius of curvature.
- The image distance v is given as 2R.
- The object distance u is initially considered to be at infinity since the beam is parallel.
Substituting n1, n2, and v into the lens maker's formula:
n2R−1∞=n−1R
Since 1∞=0, the equation simplifies to:
n2R=n−1R
Cross-multiplying gives:
n=2(n−1)
Expanding this:
n=2n−2
Rearranging gives:
2=2n−n
2=n
Thus, the refractive index n is:
n=43
Similar Questions
A parallel beam of light falls on a solid tranparent sphere.
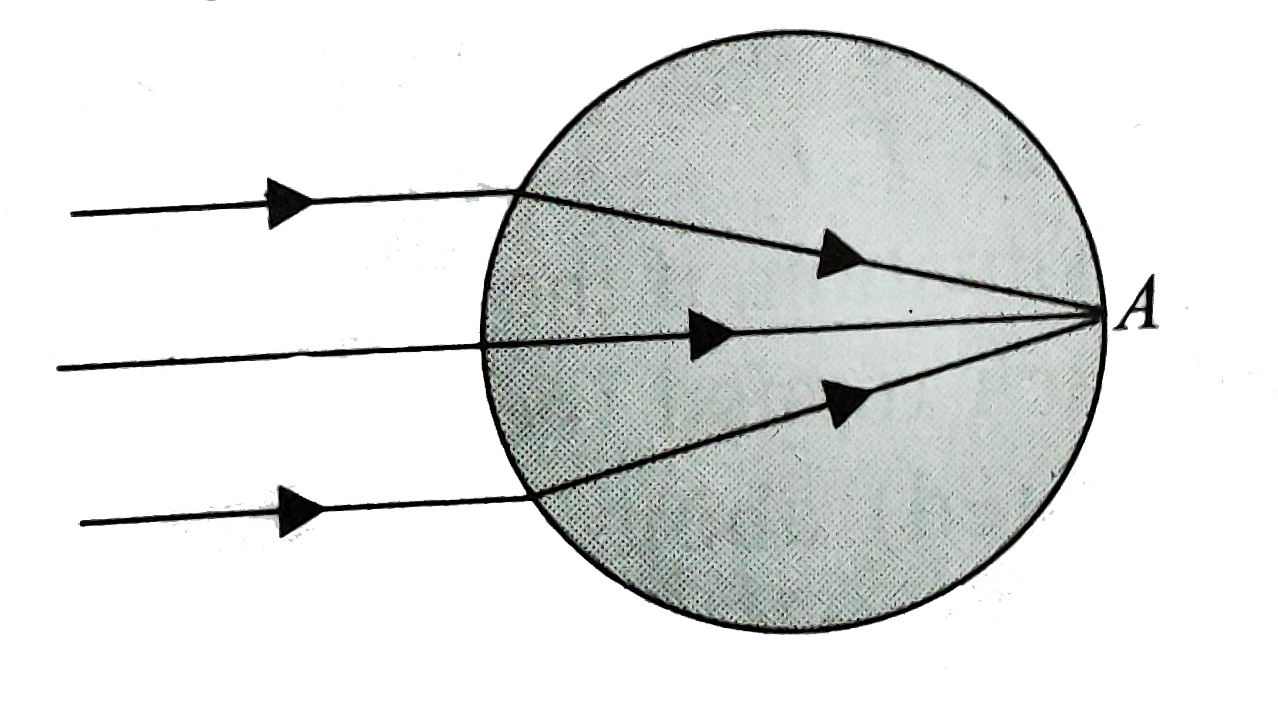
Q. Which is corret?
View SolutionA parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index μ, the thin beam can be focussed at centre of sphere.
View SolutionA narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index if the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
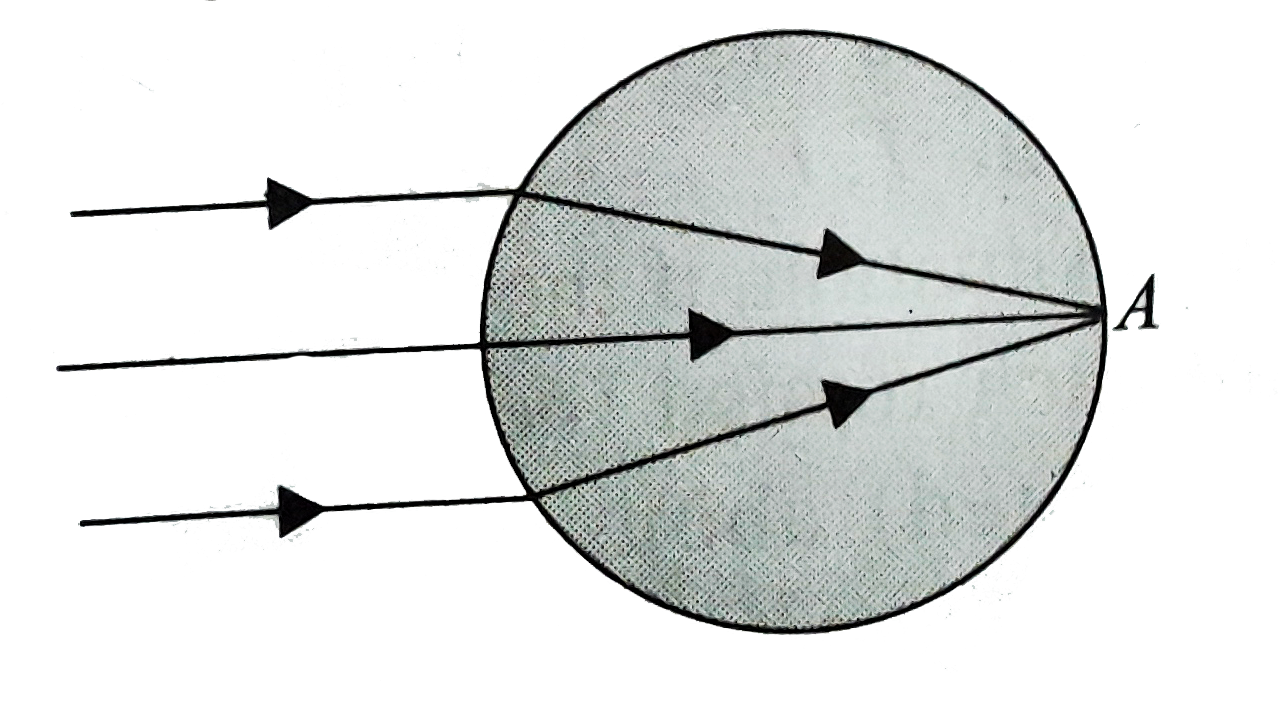
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
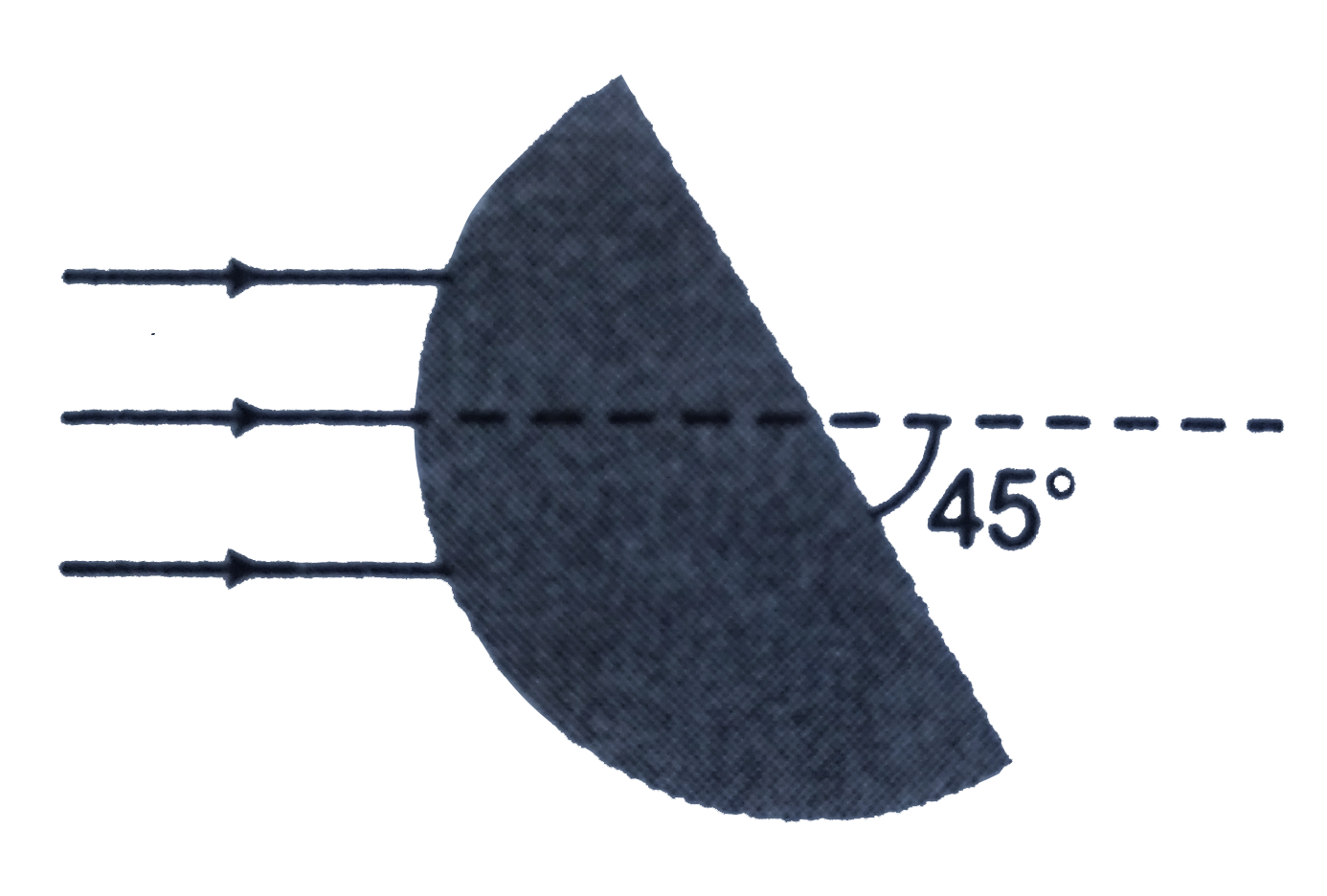
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
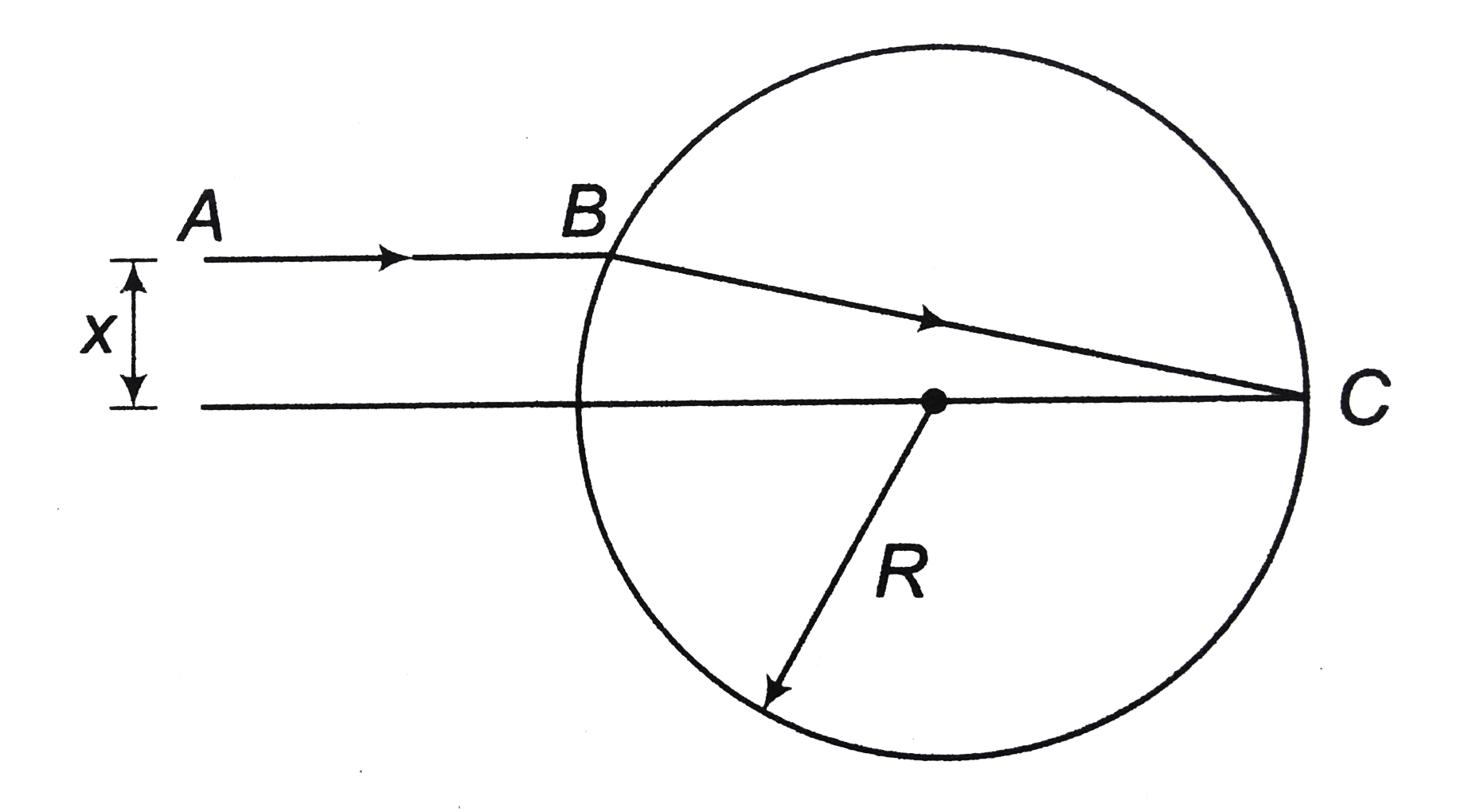
View SolutionA spherical ball of transparent material has index of refractionμ. A narrow beam of light AB is aimed as shown. What must the index of refraction be in order that the light is focused at the point C on the opposite end of the diameter from where the light entered? Given that x>>R.
View Solution
