A point object 'O' is at the center of curvature of a concave mirror. The mirror starts to move at a speed u, in a direction perpendicular to the principal axis. Then, the initial velocity of the image is
2u, in the direction opposite to theat of mirror's velocity
2u, in the direction same as that of mirror's velocity
zero
u, in the direction same as that of mirror's velocity
The correct Answer is:b.
To solve the problem of finding the initial velocity of the image when a concave mirror moves with a speed u in a direction perpendicular to the principal axis, we can follow these steps:
1. Understand the Setup:
- A point object O is located at the center of curvature C of a concave mirror.
- The image formed by the concave mirror when the object is at the center of curvature is also at the center of curvature, inverted, and of the same size.
2. Identify the Initial Conditions:
- The object is at rest, and the mirror is moving upwards with a speed u.
3. Use the Magnification Formula:
- The magnification m of the mirror is given by the formula:
m=−vu
- Here, v is the image distance, and u is the object distance. Since both the object and image are at the center of curvature, we have v=u.
4. Differentiate the Magnification Equation:
- Differentiate the magnification equation with respect to time t:
dmdt=−(dvdt⋅1u−vu2⋅dudt)
- Since u is constant (the object is stationary), dudt=0.
5. Relate the Velocities:
- The height of the object H0 and the height of the image Hi are equal when the object is at the center of curvature. Thus, we can write:
dH0dt=−dHidt
- Let vo be the velocity of the object (which is 0) and vi be the velocity of the image.
6. Express the Velocities:
- Since the object is stationary, we have:
vo=0(object is at rest)
- The mirror moves with velocity u, so we can express the velocity of the image as:
vi−u=−(−u)(since the object is at rest)
- Rearranging gives:
vi=2u
7. Conclusion:
- The initial velocity of the image is 2u in the direction of the mirror's motion.
Final Answer:
The initial velocity of the image is 2u.
- A point object O is located at the center of curvature C of a concave mirror.
- The image formed by the concave mirror when the object is at the center of curvature is also at the center of curvature, inverted, and of the same size.
- The object is at rest, and the mirror is moving upwards with a speed u.
- The magnification m of the mirror is given by the formula:
m=−vu
- Here, v is the image distance, and u is the object distance. Since both the object and image are at the center of curvature, we have v=u.
- Differentiate the magnification equation with respect to time t:
dmdt=−(dvdt⋅1u−vu2⋅dudt)
- Since u is constant (the object is stationary), dudt=0.
- The height of the object H0 and the height of the image Hi are equal when the object is at the center of curvature. Thus, we can write:
dH0dt=−dHidt
- Let vo be the velocity of the object (which is 0) and vi be the velocity of the image.
- Since the object is stationary, we have:
vo=0(object is at rest)
- The mirror moves with velocity u, so we can express the velocity of the image as:
vi−u=−(−u)(since the object is at rest)
- Rearranging gives:
vi=2u
- The initial velocity of the image is 2u in the direction of the mirror's motion.
The initial velocity of the image is 2u.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A point object on the principal axis at a distance 1.5 cm in front of concave mirror of radius of curvature 20 cm has velocity 2mm/s is perpendicular to the principal axis. The velocity of image at that instant will be
View SolutionAn object is between the principal focus and the centre of curvature of a concave mirror. The image formed is real and :
View SolutionWhen the object is at centre of curvature of a concave mirror, its image is formed at the centre of curvature. ____
View SolutionThe image of an exend object placed perpendicular to the principal axis of a mirror, will be erect if
View SolutionAn object of length 2.5 cm is placed at a distance of 1.5 f from a concave mirror where f is the magnitude of the focal length of the mirror. The length of the object is perpendicular to the principal axis. Find the length of the image. Is the image erect to inverted?

View SolutionA point object at a distance 5R/3 from the pole of a concave mirror. R is the radius of curvature of mirror. Point object oscillates with amplitude of 1mm perpendicular to the principal axis.

The amplitude of image is
View SolutionA point object at a distance 5R/3 from the pole of a concave mirror. R is the radius of curvature of mirror. Point object oscillates with amplitude of 1mm perpendicular to the principal axis.
Position of image when object is at O is :
(3/7)R
(5/7)R
(2/7)R
(4/7)R
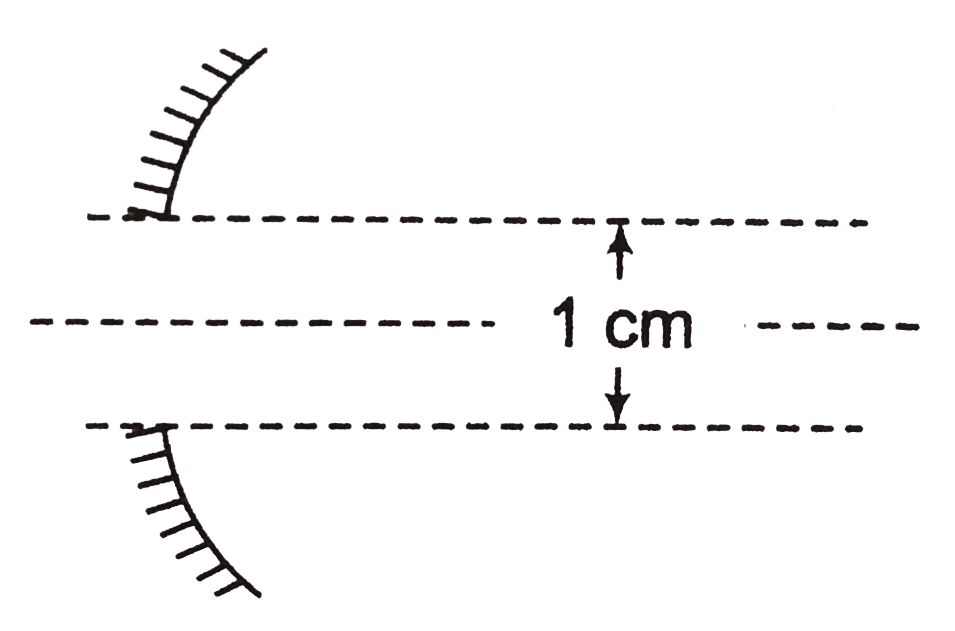
View SolutionConcave mirror forms the real image of a point source lying on the optical axis at a distance of 50 cm from the mirror. The focal length of the mirror is 25 cm. The mirror is cut into and its halves are drawn a distance of 1 cm apart in a direction perpendicular to the optical axis. How will the image formed by the halves of the mirror be arranged?
View SolutionA linear object AB is placed along the axis of a concave mirror. This object is moving towards the mirror with speed U. The speed of the image of the point A is 4U and the speed of the image of B is alSO 4U btu in opposite direction. If the center of the line AB is at a distance L from the mirror then find out the length of the object.

View SolutionA point object at a distance 5R/3 from the pole of a concave mirror. R is the radius of curvature of mirror. Point object oscillates with amplitude of 1mm perpendicular to the principal axis.

Phase difference between motion of object and image when object crosses the principal axis is
View Solution
