The given lens is broken into four parts rearranged as shown. If the initial focal length is f, then after rearrangement the equivalent focal length is

f
f/2
f/4
4f
The correct Answer is:b.
Cutting a lens in transverse direction double their focal length, i.e., 2f.
Using the formula of equivalent focal length,
1f=1f1+1f2+1f3+1f4
We get equivalent focal length as f2 .
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
The given equi-convex lens is broken into four parts and rearranged as shwon. If the initial focal length is f, then after rearrangement the equivalent focal length is

View SolutionFind the focal length of the lens used.
View SolutionA convex lens is in contact with a concave lens. The magnitude of the ration of their focal lengths is 2/3. Their equivalent focal length is 30cm. What are their individual focal lengths?
View SolutionA change in the focal length of the eye lens is brought by.
View SolutionTwo plano-convex lenses of equal focal lengths are arranged as shown
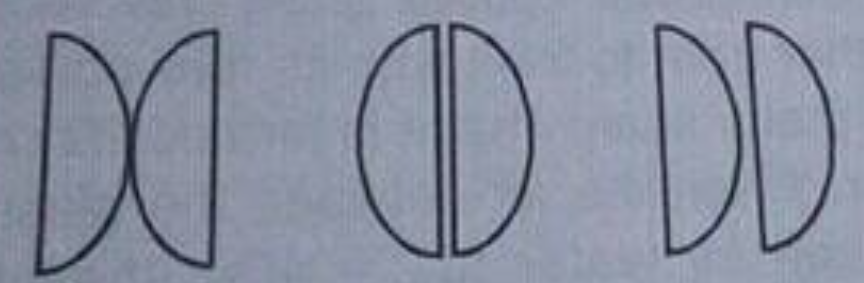
The ratio of the combined focal lengths is
View SolutionFind the focal length of the lens shown in Fig.
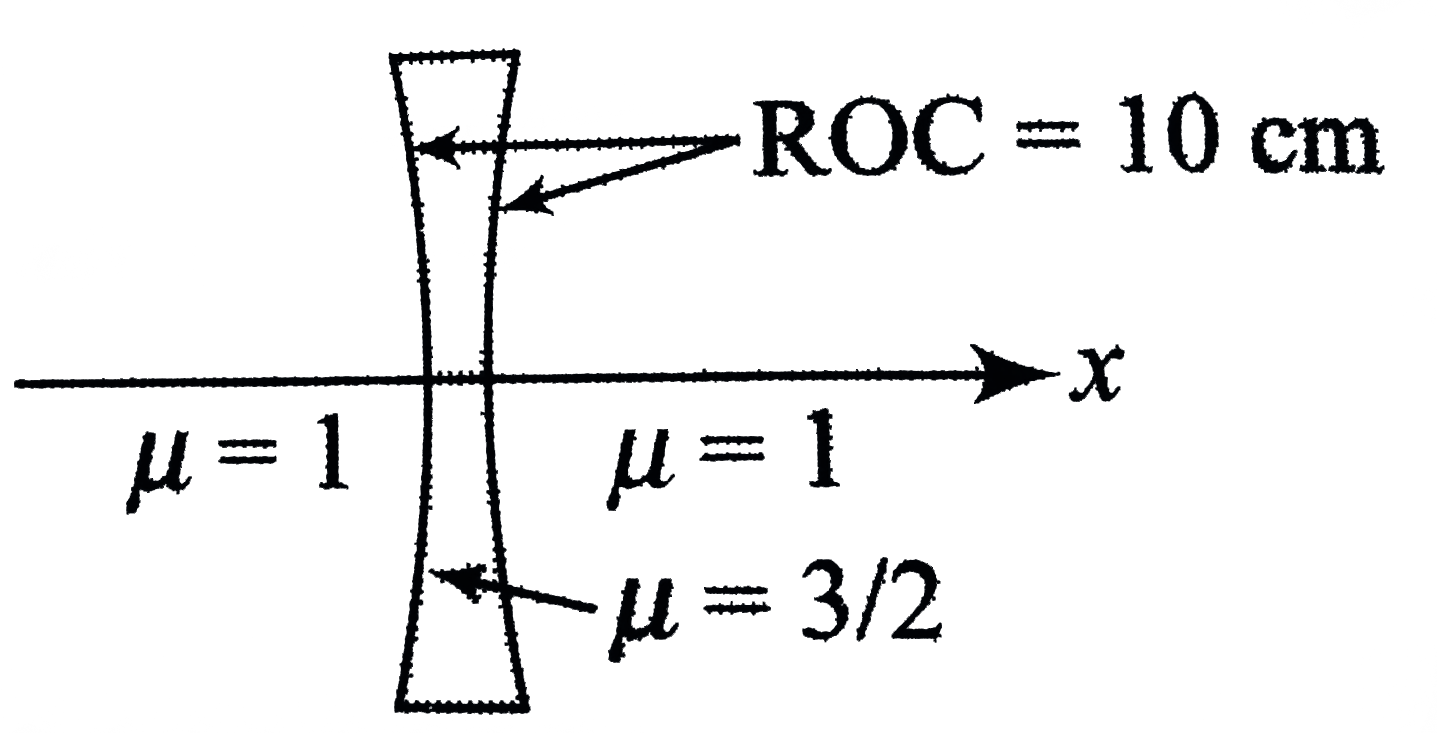
View SolutionWhen a thin convex lens is put in contact with a thin concave lens of the same focal length (f), then the resultant combination has focal length equal to
View SolutionFind the focal length of the lens shown in the Fig..
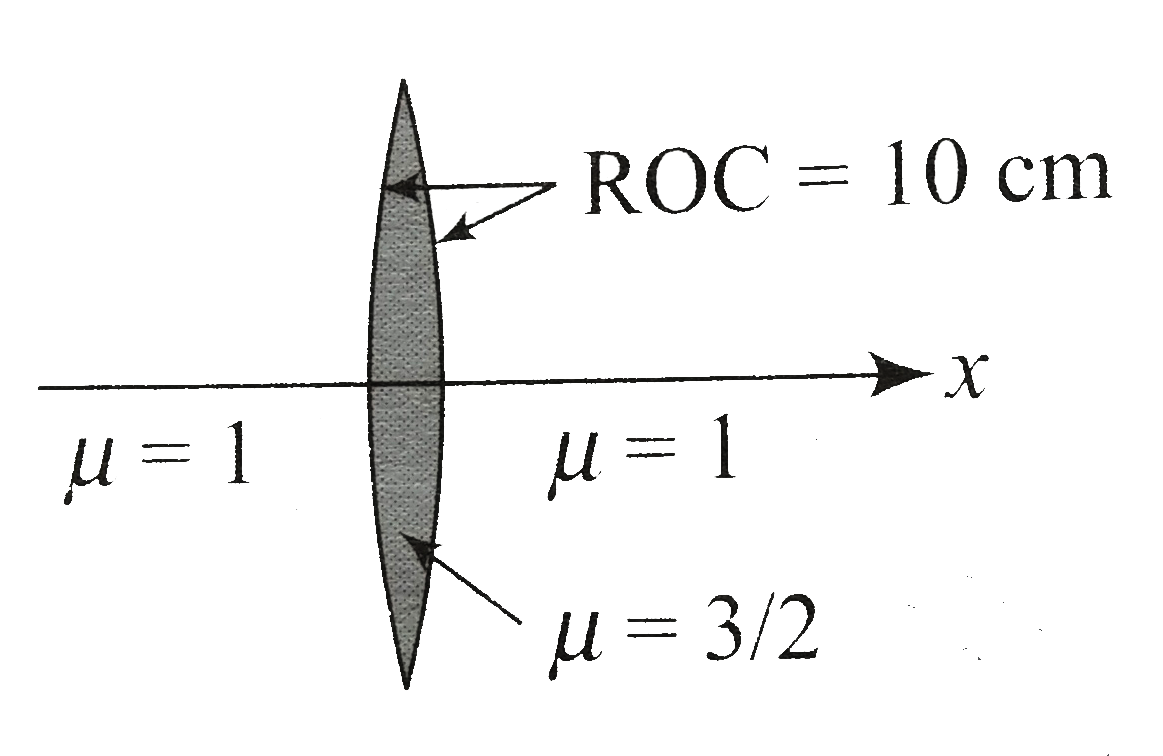
View SolutionA convex lens is in contact with a concave lens. The magnitude of the ratio of their powers is 32. Their equivalent focal length is 30 cm. What are their individual focal lengths?
View SolutionIf the focal length of the objective lens is increased then Magnifying power
View Solution
