In the above question, if the rays were to converge between F and C of mirror, then find the nature of final image formed
real
virtual
erect
inverted
The correct Answer is:b.,d.
To solve the problem of determining the nature of the final image formed when rays converge between the focal point (F) and the center of curvature (C) of a mirror, we can follow these steps:
1. Understanding the Setup:
- We have a concave mirror with a focal point (F) and a center of curvature (C).
- The rays converge at a point between F and C.
2. Using the Mirror Formula:
- The mirror formula is given by:
1f=1v+1u
- Rearranging gives:
v=u⋅fu−f
- Here, u is the object distance (which is negative for real objects in mirror conventions), and f is the focal length (negative for concave mirrors).
3. Identifying the Sign of Distances:
- Since the rays converge between F and C, we know that u (the object distance) is greater than f (the focal length) but less than C (the center of curvature).
- Thus, u<C and u>f.
4. Calculating the Image Distance (v):
- Since u is greater than f, substituting into the rearranged mirror formula shows that v will be greater than 0 (indicating a real image).
- This means that the image is formed on the same side as the object.
5. Determining the Nature of the Image:
- Since v>0, the image is real and inverted.
- The image is also formed between F and C, which indicates it is larger than the object.
6. Calculating the Magnification (M):
- The magnification formula for mirrors is given by:
M=−vu
- Since v>0 and u<0 (as per mirror conventions), the magnification M will be negative, indicating that the image is inverted.
Conclusion:
- The final image formed is real and inverted.
- We have a concave mirror with a focal point (F) and a center of curvature (C).
- The rays converge at a point between F and C.
- The mirror formula is given by:
1f=1v+1u
- Rearranging gives:
v=u⋅fu−f
- Here, u is the object distance (which is negative for real objects in mirror conventions), and f is the focal length (negative for concave mirrors).
- Since the rays converge between F and C, we know that u (the object distance) is greater than f (the focal length) but less than C (the center of curvature).
- Thus, u<C and u>f.
- Since u is greater than f, substituting into the rearranged mirror formula shows that v will be greater than 0 (indicating a real image).
- This means that the image is formed on the same side as the object.
- Since v>0, the image is real and inverted.
- The image is also formed between F and C, which indicates it is larger than the object.
- The magnification formula for mirrors is given by:
M=−vu
- Since v>0 and u<0 (as per mirror conventions), the magnification M will be negative, indicating that the image is inverted.
- The final image formed is real and inverted.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
In the above question, if the rays were to converge beyond C, then find the nature of final image formed.
View SolutionIn Figure., find the position of final image formed.
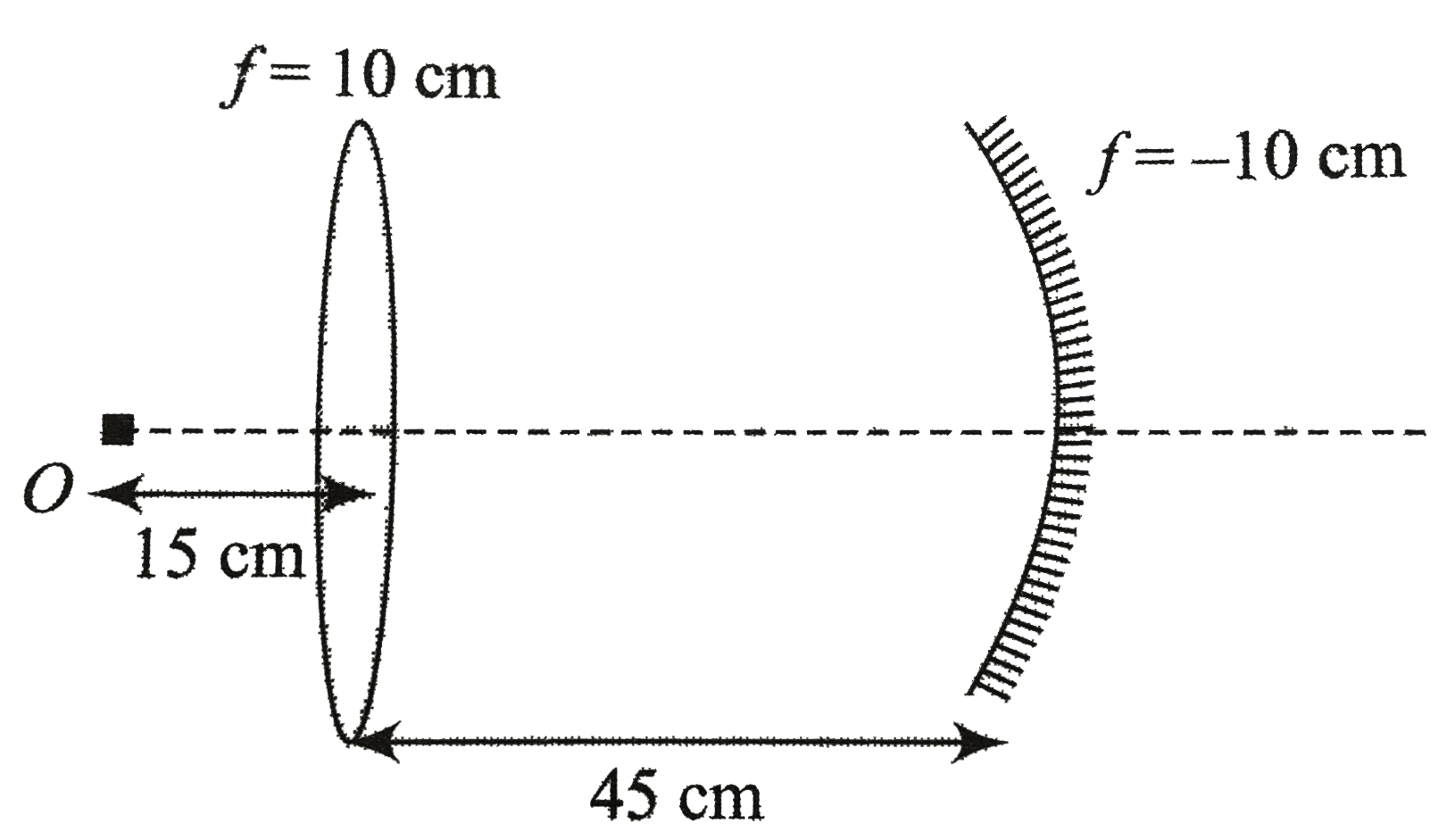 View Solution
View SolutionIn Figure. , find the position of final image formed.
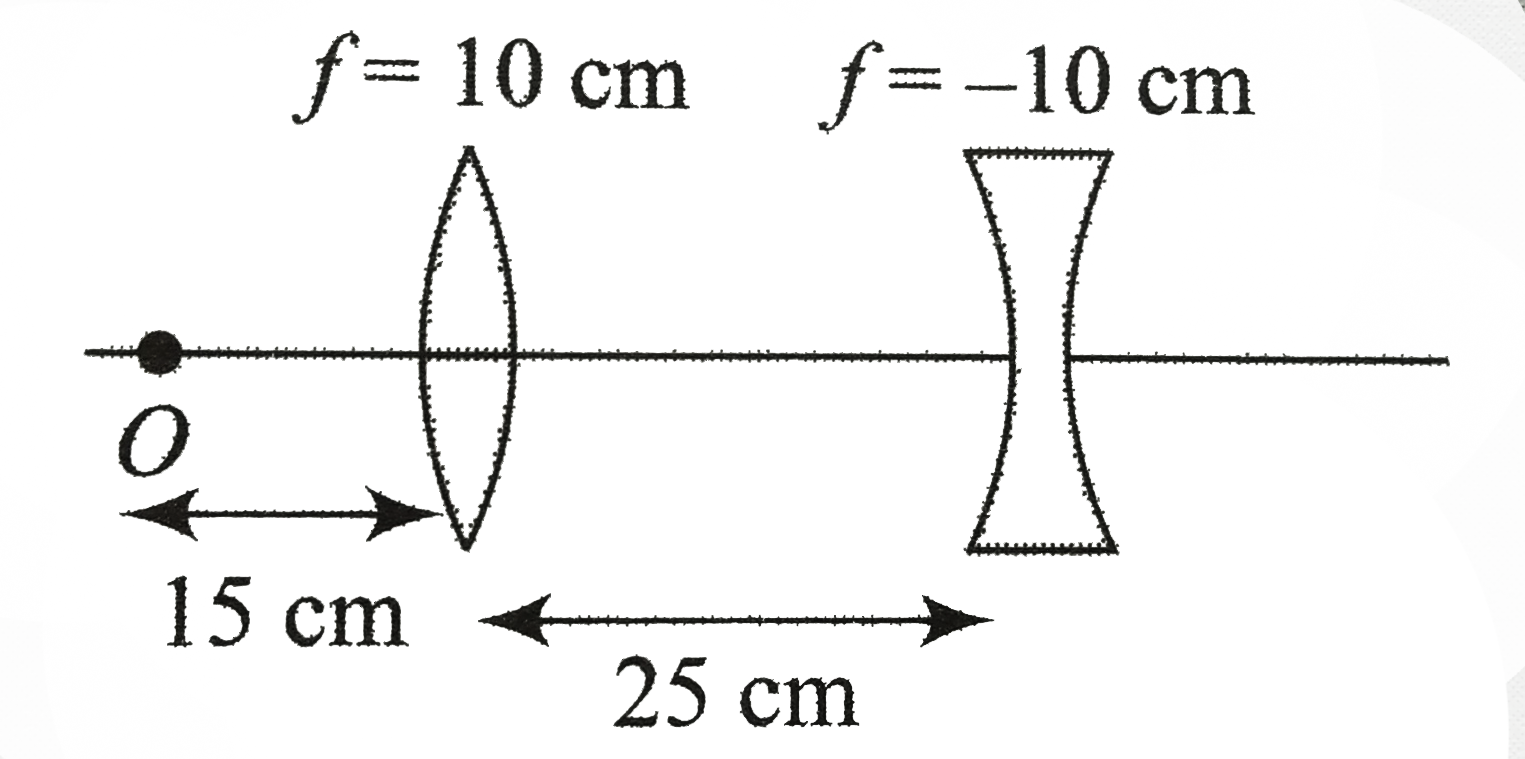 View Solution
View SolutionAn object is placed in front of a concave mirror between the pole and the focus of the mirror. What is the nature of the image formed by the mirror ?
View SolutionConverging rays strike a spherical convex mirror such that they can form the Image (in the absence of mirror) between pole and focus. Now what can you say about final image formed by mirror?
 View Solution
View SolutionWhen an object is placed between two parallel mirrors, then number of images formed are
View SolutionA point object is placed 33cm from a convex mirror of curvature radius =40cm A glass plate of thickness 6cm and refractive index 2.0 placed between the object and mirror,close to the mirror,find the distance of final image form the object?
View SolutionThe given ray diagram illustrates the experimental set up for the determination of the focal length of a converging lens using a plane mirror.
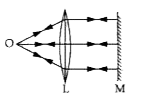
state the magnification of the image formed .View SolutionFigure shows a point object and a diverging lens
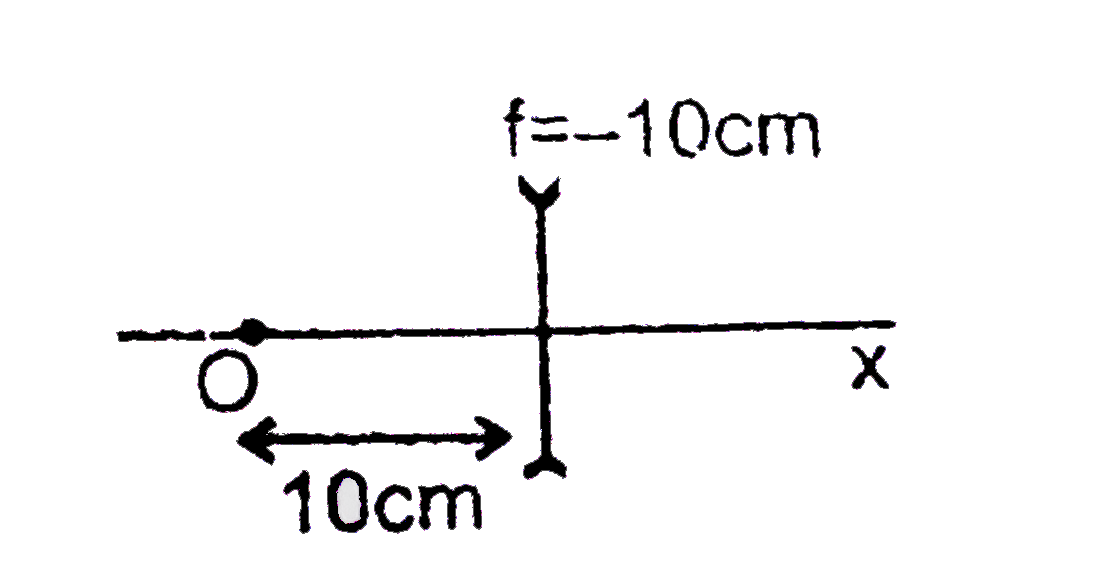
Find the final image formed.View SolutionIn example above, find the potential difference between points F and C.
View Solution

